高三年级数学第一次调研考试
数学试题
参考公式:
球的体积公式为![]() ,其中
,其中![]() 为球的半径.
为球的半径.
柱体体积公式为![]() .
.
锥体体积公式为![]() .
.
线性回归方程的系数公式为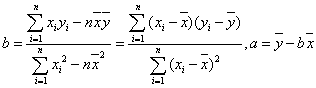 .
.
必做题部分
(本部分满分160分,考试时间120分钟)
一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题纸的指定位置上.
1.![]() = ▲ .
= ▲ .
2.函数![]() 的导函数
的导函数![]() ▲ .
▲ .
3.抛物线y2=4x的焦点坐标是 ▲ .
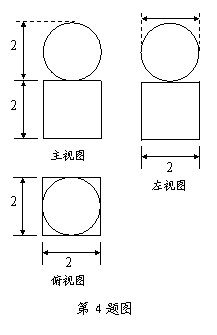
4.一个几何体的三视图如图所示,则该几何体的体积等于 ▲ .
5.已知两条直线![]() 和
和![]() 互相垂直,则
互相垂直,则![]() 等于 ▲ .
等于 ▲ .
6.在等腰直角三角形ABC中,在斜边AB上任取一点M,则AM>AC的概率是 ▲ .
7.如果实数![]() 满足不等式组
满足不等式组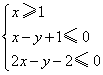 ,则
,则![]() 的最小值为 ▲ .
的最小值为 ▲ .
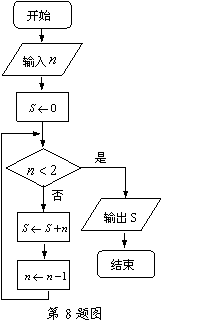
8.阅读如图所示的程序框,若输入的![]() 是100,则输出的变量
是100,则输出的变量![]() 的值是 ▲ .
的值是 ▲ .![]()
9.在△![]() 中,
中,![]() ,
, ![]() ,若
,若![]() ,则
,则![]() = ▲ .
= ▲ .
10.定义:区间![]() 的长度为
的长度为![]() .已知函数
.已知函数![]() 定义域为
定义域为![]() ,值域为
,值域为![]() ,则区间
,则区间![]() 的长度的最大值为 ▲ .
的长度的最大值为 ▲ .
11.设![]() 是正项数列,其前
是正项数列,其前![]() 项和
项和![]() 满足:
满足:![]() ,则数列
,则数列![]() 的通项公式
的通项公式![]() =
=
▲ .
12.若函数![]() (
(![]() )在
)在![]() 上的最大值为
上的最大值为![]() ,则
,则![]() 的值为 ▲ .
的值为 ▲ .
13.从椭圆上一点A看椭圆的两焦点![]() 的视角为直角,
的视角为直角,![]() 的延长线交椭圆于B,且
的延长线交椭圆于B,且![]() ,则椭圆的离心率为 ▲ .
,则椭圆的离心率为 ▲ .
14.某同学在研究函数 f (x) = (![]() ) 时,分别给出下面几个结论:
) 时,分别给出下面几个结论:
①等式![]() 在
在![]() 时恒成立; ②函数 f (x) 的值域为 (-1,1);
时恒成立; ②函数 f (x) 的值域为 (-1,1);
③若x1≠x2,则一定有f (x1)≠f (x2); ④函数![]() 在
在![]() 上有三个零点.
上有三个零点.
其中正确结论的序号有 ▲ .(请将你认为正确的结论的序号都填上)
二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内.
15.(本小题满分14分)已知向量![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() ;(7分)
;(7分)
(Ⅱ)求![]() 的最大值.(7分)
的最大值.(7分)
16.(本小题满分14分)某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;(5分)
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程![]() ;(6分)
;(6分)
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?(3分)
 (参考公式:
(参考公式: 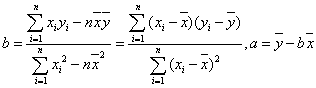 )
)
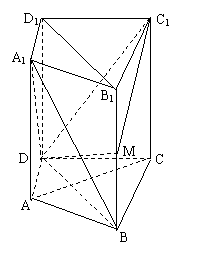
17.(本小题满分15分)如图所示,在直四棱柱![]() 中,
中,![]() ,
, ![]() ,点
,点![]() 是棱
是棱![]() 上一点.
上一点.
(Ⅰ)求证:![]() 面
面![]() ;(5分)
;(5分)
(Ⅱ)求证:![]() ;(5分)
;(5分)
(Ⅲ)试确定点![]() 的位置,使得平面
的位置,使得平面![]()
![]() 平面
平面![]() . (5分)
. (5分)
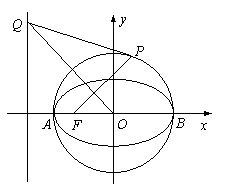 18.(本小题满分15分)已知圆O:
18.(本小题满分15分)已知圆O:![]() 交
交![]() 轴于A,B两点,曲线C是以
轴于A,B两点,曲线C是以![]() 为长轴,离心率为
为长轴,离心率为![]() 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
(Ⅰ)求椭圆C的标准方程;(5分)
(Ⅱ)若点P的坐标为(1,1),求证:直线PQ与圆![]() 相切;(5分)
相切;(5分)
(Ⅲ)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由. (5分)
19.(本小题满分16分)如图是一个面积为1的三角形,现进行如下操作.第一次操作:分别连结这个三角形三边的中点,构成4个三角形,挖去中间一个三角形(如图①中阴影部分所示),并在挖去的三角形上贴上数字标签“1”;第二次操作:连结剩余的三个三角形三边的中点,再挖去各自中间的三角形(如图②中阴影部分所示),同时在挖去的3个三角形上都贴上数字标签“2”;第三次操作: 连结剩余的各三角形三边的中点,再挖去各自中间的三角形,同时在挖去的三角形上都贴上数字标签“3”;……,如此下去.记第![]() 次操作后剩余图形的总面积为an.
次操作后剩余图形的总面积为an.

(Ⅰ)求![]() 、
、![]() ;(4分)
;(4分)
(Ⅱ)欲使剩余图形的总面积不足原三角形面积的![]() ,问至少经过多少次操作?(5分)
,问至少经过多少次操作?(5分)
(Ⅲ)求第n次操作后,挖去的所有三角形上所贴标签上的数字和Sn.(7分)
20.(本小题满分16分)设函数![]() (其中
(其中![]() )的图象在
)的图象在![]() 处的切线与直线y=-5x+12平行.
处的切线与直线y=-5x+12平行.
(Ⅰ)求![]() 的值;(4分)
的值;(4分)
(Ⅱ)求函数![]() 在区间[0,1]的最小值;(4分)
在区间[0,1]的最小值;(4分)
(Ⅲ)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
试根据上述(Ⅰ)、(Ⅱ)的结论证明:![]() . (8分)
. (8分)
附加题部分
(本部分满分40分,考试时间30分钟)
一、选做题:请在下列4小题中任做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内,多做者按所做的前2题给分.
1.(选修4—1:几何证明选讲)已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
(Ⅰ)求证:FB=FC;
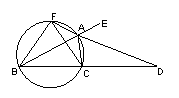 (Ⅱ)若AB是△ABC外接圆的直径,
(Ⅱ)若AB是△ABC外接圆的直径,![]() ,BC=6,求AD的长.
,BC=6,求AD的长.
2.(选修4—2:矩阵与变换)已知矩阵![]() ,其中
,其中![]() ,若点
,若点![]() 在矩阵
在矩阵![]() 的变换下得到的点
的变换下得到的点![]()
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求矩阵![]() 的特征值及特征向量.
的特征值及特征向量.
3.(选修4—4:坐标系与参数方程)从极点![]() 作直线与另一直线
作直线与另一直线![]() 相交于点
相交于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设![]() 为
为![]() 上的任意一点,试求
上的任意一点,试求![]() 的最小值.
的最小值.
4.(选修4—5:不等式选讲)已知![]() 为正数,且满足
为正数,且满足![]() ,
,
求证:![]() .
.
二、必做题:本大题共2小题,每小题10分,计20分,请把答案写在答题纸的指定区域内.
5.求由曲线y=x3,直线x=1,x=2及y=0所围成的曲边梯形的面积.
6.一个人随机地将编号为1,2,3的三个小球放入编号为1,2,3的三个盒子中去,每个盒子放入一个小球,当球的编号与盒子的编号相同时叫做放对了,否则叫做放错了,设放对了的个数有![]() 种.
种.
(Ⅰ)求![]() 的分布列;
的分布列;
(Ⅱ)求![]() 的期望值.
的期望值.