高三年级数学第四次调查测试
|
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么![]()
如果事件![]() 在一次试验中发生的概率是
在一次试验中发生的概率是![]() ,那么
,那么![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率
次的概率![]()
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,恰有一项是符合题目要求的,请把正确答案填涂在答题卡的指定位置。
1.已知集合![]() ,
,![]() ,则集合
,则集合![]() 的真子集个数为 ( )
的真子集个数为 ( )
A 32个 B 31个 C 64个 D 63个
2.已知条件p:![]() 内是增函数,条件q:
内是增函数,条件q:![]() ,则p是q成立的( )
,则p是q成立的( )
A 充要条件 B 充分不必要条件
C 必要不充分条件 D 既不充分又不必要条件
3.若把函数![]() 的图象沿向量
的图象沿向量![]() 平移,使所得的图象关于
平移,使所得的图象关于![]() 轴对称,则
轴对称,则![]() 的最小值是
( )
的最小值是
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
4.下列命题正确的是 ( )
A 垂直于同一平面的两个平面互相平行
B
经过平面![]() 的一条斜线的平面
的一条斜线的平面![]() 与平面
与平面![]() 一定不垂直
一定不垂直
C 若a,b是异面直线,则过直线a一定不能作与直线b垂直的平面
D
若平面![]() ,
,![]() 相交但不垂直,则平面
相交但不垂直,则平面![]() 内任意一条直线都与平面
内任意一条直线都与平面![]() 不垂直
不垂直
5.已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,则
( )
,则
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
6.已知二项式(![]() 的展开式中含有
的展开式中含有![]() 的项, 则n的一个可能值是
( )
的项, 则n的一个可能值是
( )
A 6 B 9 C 8 D 10
7.已知变量![]() 满足约束条件
满足约束条件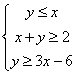 ,则目标函数
,则目标函数![]() 的最大值为( )
的最大值为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
8.已知二面角![]() 的平面角为
的平面角为![]() ,
,![]() ,
,![]() ,
,![]() 为垂足,设
为垂足,设![]() ,
,![]() ,
,
![]() 到棱
到棱![]() 的距离分别为
的距离分别为![]() 、
、![]() ,当
,当![]() 变化时,点
变化时,点![]() 的轨迹是
( )
的轨迹是
( )
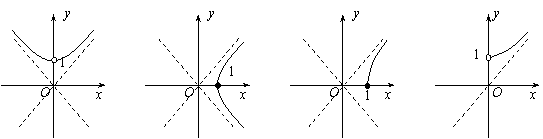 |
A B C D
9.已知函数![]() ,正实数a、b、c成公差为正数的等差数列,且满足
,正实数a、b、c成公差为正数的等差数列,且满足![]() ,若实数d 是方程
,若实数d 是方程![]() 的一个解,那么下列四个判断:①
的一个解,那么下列四个判断:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 中有可能成立的个数为
( )
中有可能成立的个数为
( )
A 1 B 2 C 3 D 4
10.已知实数![]() ,其中
,其中![]() ,且
,且![]() ,则实数对
,则实数对![]() 表示平面上不同点的个数为 ( )
表示平面上不同点的个数为 ( )
A ![]() 个
B
个
B ![]() 个
C
个
C ![]() 个
D
个
D ![]() 个
个
二、填空题:本大题共6小题,每小题5分,共30分.请将答案填写在答题卡的指定位置.
11.将一组样本数据中的每一个数据都乘以2,再都减去80,得到一组新的样本数据. 若求得新的样本数据的平均数是1.2,方差是4.4,则原样本数据的平均数为 ▲ ,方差为 ▲ 。
12.已知函数![]() 在区间
在区间![]() 内存在极值,则实数
内存在极值,则实数![]() 的取值范围为 ▲ 。
的取值范围为 ▲ 。
13.已知平面内的向量![]() 、
、![]() 满足:
满足:![]() =
=![]() =1,
=1, ![]() 与
与![]() 的夹角为
的夹角为![]() ,又
,又![]() =x
=x![]() +y
+y![]() ,
,

![]() ,
,![]() ,则点
,则点![]() 的集合所表示的图形面积为 ▲ 。
的集合所表示的图形面积为 ▲ 。
14.已知椭圆![]() 上的点
上的点![]() 与
与![]() (i=1,2,3)关于x轴对称,且
(i=1,2,3)关于x轴对称,且![]() 为该椭圆的一个焦点,则
为该椭圆的一个焦点,则![]() ▲ 。
▲ 。
15.如图为类似课本研究性学习课题《杨辉三角》中的竖直平面内一些通道,
图中粗线条均表示通道,一钢珠从入口处自上而下沿通道自由落入乙处
的概率是 ▲ 。 (第15题图)
16.已知直线![]() 相切,其中m、
相切,其中m、![]() ,试写出所有满足条件的有序实数对(m,n): ▲
。
,试写出所有满足条件的有序实数对(m,n): ▲
。
三、解答题:本大题共5小题,共70分. 解答应写出文字说明,证明过程或演算步骤。请将解题过程写在答题卡指定的方框内。
17.(本小题满分12分)
已知△ABC的面积为![]() ,且满足
,且满足![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求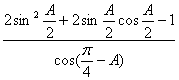 的值。
的值。
18.(本小题满分14分)
已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 为椭圆
为椭圆![]() 上的任意一点,满足
上的任意一点,满足![]() 的最小值为
的最小值为![]() ,过
,过![]() 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
19.(本小题满分14分)
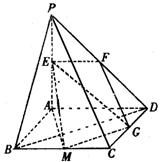
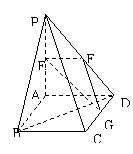 如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
如图,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点。
|
(Ⅱ)求异面直线EG与BD所成的角;
(Ⅲ)在线段CD上是否存在一点Q,使得A点到平面EFQ的距离为0.8,若存在,求出CQ的值;若不存在,请说明理由。
20.(本小题满分14分)
已知![]() ,函数
,函数![]()
(Ⅰ)当t=1时,求函数![]() 在区间[0,2]的最值;
在区间[0,2]的最值;
(Ⅱ)若![]() 在区间[-2,2]上是单调函数,求t的取值范围;
在区间[-2,2]上是单调函数,求t的取值范围;
(Ⅲ))是否存在常数t,使得任意![]() 恒成立,若存在,请求出t,若不存在请说明理由.
恒成立,若存在,请求出t,若不存在请说明理由.
21. (本小题满分16分)
设集合![]() 是满足下列两个条件的无穷数列
是满足下列两个条件的无穷数列![]() 的集合:
的集合:
①![]() ②
②![]()
![]() 是与
是与![]() 无关的常数.
无关的常数.
(Ⅰ)若![]() 是等差数列,
是等差数列,![]() 是其前n项的和,
是其前n项的和,![]() ,证明:
,证明:![]() ;
;
(Ⅱ)设数列![]() 的通项为
的通项为![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅲ))设数列![]() 的各项均为正整数,且
的各项均为正整数,且![]() ,试证
,试证![]() 。
。
命题:周志国 冯建国
审校:冯建国 刘兴东 刘其鹿
高三年级数学第四次调查测试
数学试题参考答案与评分标准
说明:
一、本解答给出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。
二、对计算题,当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定后续部分的给分,但不得超过该部分正确解答所给分数的一半;如果后续部分的解答存在较严重的错误,则不再给分。
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数。
四、每题只给整数分数,选择题和填空题不给中间分。
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | C | D | A | A | B | C | B | D |
二、填空题:
11.40.6,1.1 12.![]() 13.
13.![]() 14.30 15.
14.30 15. ![]() 16.(1,1),(2,2),(3,4),(4,8)
16.(1,1),(2,2),(3,4),(4,8)
三、解答题:
17.(Ⅰ)![]() , ①
…………………2分
, ①
…………………2分
又![]() , ∴
, ∴![]() ②
……………… 4分
②
……………… 4分
由①、②得![]() …………………………………………………………… 6分
…………………………………………………………… 6分
(Ⅱ)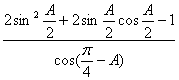
![]() ……………………………………… 8分
……………………………………… 8分
![]() …………………………………………………………………… 10分
…………………………………………………………………… 10分
![]()
![]() …………………………………………………………………………12分
…………………………………………………………………………12分
18.(Ⅰ)设点![]()
![]() ,则
,则![]() ,
,
![]() ,
,![]()
![]() ,又
,又![]() ,
,
![]() ,∴椭圆的方程为:
,∴椭圆的方程为:![]() …………………………………………7分
…………………………………………7分
(Ⅱ)当过![]() 直线
直线![]() 的斜率不存在时,点
的斜率不存在时,点![]() ,则
,则![]() ;
;
当过![]() 直线
直线![]() 的斜率存在时,设斜率为
的斜率存在时,设斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
设![]() ,由
,由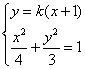 得:
得:![]()
![]() …………………………………………10分
…………………………………………10分
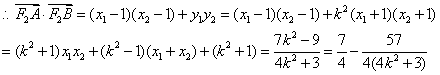
![]() ……13分
……13分
综合以上情形,得:![]() ……………………………………………………14分
……………………………………………………14分
|
∴GH∥AD∥EF,∴E,F,G,H四点共面. ……………………1分
又H为AB中点,∴EH∥PB. 又EH![]() 面EFG,PB
面EFG,PB![]() 平面EFG,
平面EFG,
∴PB∥平面EFG. ………………………………4分
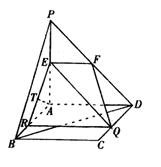
(Ⅱ)取BC的中点M,连结GM、AM、EM,则GM//BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角.……6分
在Rt△MAE中, ![]() ,
,
同理![]() ,又GM=
,又GM=![]() ,………………7分
,………………7分
∴在△MGE中,![]() ………………8分
………………8分
故异面直线EG与BD所成的角为arccos![]() ,
………………………………9分
,
………………………………9分
|
又AB∩PA=A,∴AD⊥平面PAB. ……………………………………10分
又∵E,F分别是PA,PD中点,∴EF∥AD,∴EF⊥平面PAB.
又EF![]() 面EFQ,∴面EFQ⊥面PAB. ………………………………11分
面EFQ,∴面EFQ⊥面PAB. ………………………………11分
过A作AT⊥ER于T,则AT⊥平面EFQ,
∴AT就是点A到平面EFQ的距离. ………………………………12分
设![]() ,则
,则![]()
在![]() ,
…………………………13分
,
…………………………13分
解得![]() 故存在点Q,当CQ=
故存在点Q,当CQ=![]() 时,点A到平面EFQ的距离为0.8. ……………………… 14分
时,点A到平面EFQ的距离为0.8. ……………………… 14分
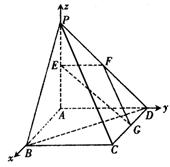
解法二:建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),
|
(Ⅰ)![]()
![]() …………1分
…………1分
设![]() , 即
, 即![]() ,
,

![]() ……………3分
……………3分
![]() ,∴PB∥平面EFG. ………………………………………………………… 4分
,∴PB∥平面EFG. ………………………………………………………… 4分
(Ⅱ)∵![]() ,
…………………………………………5分
,
…………………………………………5分
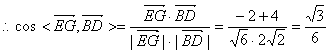 ,
……………………… 8分
,
……………………… 8分
故异面直线EG与BD所成的角为arcos![]() .
……………………………………
9分
.
……………………………………
9分
(Ⅲ)假设线段CD上存在一点Q满足题设条件,令![]()
∴点Q的坐标为(2-m,2,0),![]() ……………………………………10分
……………………………………10分
而![]() , 设平面EFQ的法向量为
, 设平面EFQ的法向量为![]() ,则
,则
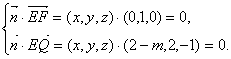
![]()
令![]() ,
……………………………………………………12分
,
……………………………………………………12分
又![]() , ∴点A到平面EFQ的距离
, ∴点A到平面EFQ的距离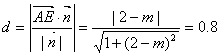 ,……13分
,……13分
即![]() ,
,![]() 不合题意,舍去.
不合题意,舍去.
故存在点Q,当CQ=![]() 时,点A到平面EFQ的距离为0.8.
……………………14分
时,点A到平面EFQ的距离为0.8.
……………………14分
20. (Ⅰ)![]() ,
,![]() ………………2分
………………2分
当![]() 时,
时,![]() , …………4分
, …………4分
(Ⅱ)![]()
![]() 是单调增函数; ………………6分
是单调增函数; ………………6分
由![]()
![]() 是单调减函数;
………………8分
是单调减函数;
………………8分
(Ⅲ)![]() 是偶函数,对任意
是偶函数,对任意![]() 都有
都有![]() 成立
成立
![]() 对任意
对任意![]() 都有
都有![]() 成立
成立
1°由(Ⅱ)知当![]() 或
或![]() 时,
时,![]() 是定义域上的单调函数,
是定义域上的单调函数,
对任意![]() 都有
都有![]() 成立
成立![]()
![]() 时,对任意
时,对任意![]() 都有
都有![]() 成立
…………10分
成立
…………10分
2°当![]() 时,
时,![]() ,由
,由![]()
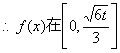 上是单调增函数
上是单调增函数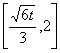 在上是单调减函数,∴对任意
在上是单调减函数,∴对任意![]() 都有
都有![]()
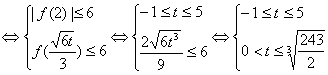
![]() 时,对任意
时,对任意![]() 都有
都有![]() 成立
………………12分
成立
………………12分
综上可知,当![]() 时,对任意
时,对任意![]() 都有
都有![]() 成立
.……14分
成立
.……14分
21、(Ⅰ)设等差数列{![]() }的公差是
}的公差是![]() ,则
,则![]() ,解得
,解得![]()
所以![]() ……………………………………2分
……………………………………2分
由![]() =-1<0
=-1<0
得![]() 适合条件①;又
适合条件①;又![]() ,所以当
,所以当![]() =4或5时,
=4或5时,![]() 取得最大值20,即
取得最大值20,即![]() ≤20,适合条件②。综上所述,
≤20,适合条件②。综上所述, ![]() …………………………………………4分
…………………………………………4分
(Ⅱ)因为![]() ,所以当n≥3时,
,所以当n≥3时,![]() ,此时数列
,此时数列![]() 单调递减;当
单调递减;当![]() =1,2时,
=1,2时,![]() ,即
,即![]()
因此数列![]() 中的最大项是
中的最大项是![]() ,所以
,所以![]() ≥7………………………………………………………8分
≥7………………………………………………………8分
(Ⅲ)假设存在正整数![]() ,使得
,使得![]() 成立,
成立,
由数列![]() 的各项均为正整数,可得
的各项均为正整数,可得![]() ……………10分
……………10分
因为![]() ……11分
……11分
由
![]() …13分
…13分
因为![]()
依次类推,可得![]() ……………………………………………15分
……………………………………………15分
又存在![]() ,使
,使![]() ,总有
,总有![]() ,故有
,故有![]() ,这与数列(
,这与数列(![]() )的各项均为正整数矛盾!
)的各项均为正整数矛盾!
所以假设不成立,即对于任意![]() ,都有
,都有![]() 成立.
………………………16分
成立.
………………………16分