高三年级数学第四次调研考试
理科数学试卷
一、填空题(本题共14小题，每题5分，共70分)
1. 函数
的定义域为 . 答案：
2. 化简(cos225 º +isin225º)2(其中i为虚数单位)的结果为 . 答案：i
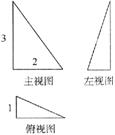3. 一个空间几何体的主视图、左视图、俯视图为直角三角形，边长如图所示，那么这个几何体的体积为
. 答案：1
4. 抛物线C的顶点为坐标原点，焦点为二次函数
的图象的顶点，则此抛物线的方程为
______.答案：
5.设函数
,其中向量
,则函数f(x)的最小正周期是
. 答案：
6. 已知回归直线斜率的估计值为1.2，样本点的中心为（4，5），则回归直线方程为 .
答案：
7. 当
时,函数
的最小值是
. 答案：—3
8. 已知圆
和直线
交于A,B两点,O是坐标原点, 若
,则
. 答案：
9. 直线
与曲线
相切于点
，则b的值为 . 答案：3
10. 与曲线
共焦点并且与曲线
共渐近线的双曲线方程为 .
答案：
11. 设
、
是异面直线，则(1)一定存在平面
，使
且∥；(2)一定存在平面，使且
；(3)一定存在平面
，使，到的距离相等；(4)一定存在无数对平面与
，使，
，且
∥；上述4个命题中正确命题的序号为 . 答案：(1) (3)
12. 球的半径为2a,一平面截得球所得小圆的面积为3
a 2,则球心到这个平面的距离为 .
答案：a
13. 把1，2，……，100这100个自然数任意分成10组，每组10个数，将每组中最大的数取出来，所得10个数的和为S.若S的最大值为M，最小值为N，则M+N= . 答案：1505
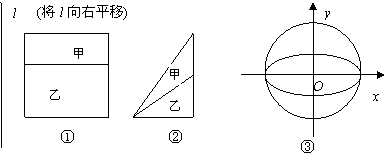
14. 我们可以运用下面的原理解决一些相关图形的面积问题：如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k，那么甲的面积是乙的面积的k倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是
与
，运用上面的原理，图③中椭圆的面积为 .
答案：
二、解答题(本题共6小题，总分90分)
15. （本题满分14分）已知函数
，
（1）若
，求函数
的最大值与最小值；
（2）若
，且
，求的值.
答案：（1） 
，…………2分
，，
…………6分
分别在
时取得. …………8分
（2），
，
，…………11分
又
， 
. …………14分
16. （本题满分15分）如图，已知A、B、C是长轴长为4的椭圆上的三点，点A是长轴的右顶点，BC过椭圆中心O，且
·
=0，
，
（1）求椭圆的方程；
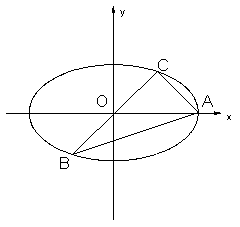（2）若过C关于y轴对称的点D作椭圆的切线DE，则AB与DE有什么位置关系？证明你的结论.
答案：（1）A（2，0），设所求椭圆的方程为：
=1(0<b<2)，
……2分
由椭圆的对称性知，OC=OB，
由·=0得，AC⊥BC，
∵BC=2AC，∴OC=AC，∴△AOC是等腰直角三角形，
∴C的坐标为（1，1）． ……4分
∵C点在椭圆上，∴
=1，∴b2=
．
所求的椭圆方程为
=1．
……8分
（2）是平行关系.…………10分
D（-1，1），设所求切线方程为y-1=k（x+1）
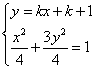，消去x，
…………12分
上述方程中判别式=
，
又
，所以AB与DE平行.…………15分
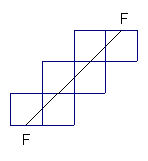
17. （本题满分15分）如图，在正方体ABCD－A1B1C1D1中，E、F为棱AD、AB的中点．
（1）求证：EF∥平面CB1D1；
（2）求证：平面CAA1C1⊥平面CB1D1．
（3）如果AB=1，一个点从F出发在正方体的表面上依次经过棱BB1、B1C1、C1D1、D1D、DA上的点，又回到F，指出整个线路的最小值并说明理由.
答案：（1）证明:连结BD.
在长方体
中，对角线
.
又
E、F为棱AD、AB的中点，
.
.
又B1D1平面
，
平面
，
EF∥平面CB1D1. …………5分
（2） 在长方体中，AA1⊥平面A1B1C1D1，而B1D1平面A1B1C1D1，
AA1⊥B1D1.
又在正方形A1B1C1D1中，A1C1⊥B1D1，
B1D1⊥平面CAA1C1.
又 B1D1平面CB1D1，
平面CAA1C1⊥平面CB1D1．…………10分
（3）最小值为 
…………12分
如图，将正方体六个面展开，从图中F到F，两点之间线段最短，而且依次经过棱BB1、B1C1、C1D1、D1D、DA上的中点，所求的最小值为 .…………15分
18．（本题满分15分）
已知某公司生产品牌服装的年固定成本为10万元,每生产千件,须另投入2.7万元,设该公司年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且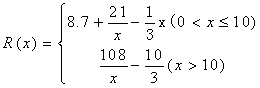
（1）写出年利润W(万元)关于年产量x(千件)的函数解析式:
（2）年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?(注:年利润=年销售收入—年总成本)
答案：（1）
时，W=R(x)-(10+2.7x)=8.7x+21-
=
当x>10时，
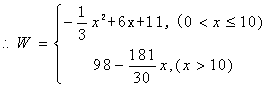…………………………………………7分
（2）①当
时，
时，W取得最大值，
②当
时，
，
是减函数，
综合①②、当
时W取最大值
当年产量为9千件时,该公司在这一品牌服装的生产中所获年利润最大。………………15分
19．（本题满分15分）已知函数y=f（x）=
.
（1）证明这个函数为偶函数；
（2）证明T=
是函数的一个周期，进而寻找函数是否有其他的周期，最后说明这个函数的周期组成什么集合.
答案：（1）对任意实数x，x与-x同为有理数或无理数，所以恒有f（x）=f（-x），又定义域关于原点对称，函数为偶函数；………………………5分
（2）当T=时，对任意实数x，x与x+同为有理数或无理数，所以恒有f（x）=f（x+），所以T=是函数的周期； …………8分
当T为有理数时，对任意实数x以及有理数T，x与x+T同为有理数或无理数，所以恒有f（x）=f（x+T），所以T是函数的周期；…………11分
当T为无理数时，f（-T）=0，f（-T+T）=f（0）=1，所以T不是函数的周期，函数的所有周期组成有理数集合
…………15分
20． （本题满分16分）幂函数y = 的图象上的点 Pn(tn2,tn)（n = 1,2,……）与 x 轴正半轴上的点 Qn 及原点 O 构成一系列正△PnQn－1Qn（Q0与O重合），记 an = QnQn－1
（1）求 a1的值；
（2）求数列 {an} 的通项公式 an;
（3）设 Sn为数列 {an} 的前 n 项和，若对于任意的实数 l∈[0,1]，总存在自然数 k，当 n≥k时，3Sn－3n + 2≥(1－l) (3an－1) 恒成立，求 k 的最小值.
答案：(1) 由 P1(t12,t1)（t > 0），… 1分,得 kOP1 = = tan = Þ t1 =
∴ P1(,) …………2分
a1 = Q1Q0 = OP1 = …………5分
(2) 设 Pn(tn2,tn)，得直线 PnQn－1的方程为：y－tn = (x－tn2)
可得 Qn－1(tn2－,0)
直线 PnQn的方程为：y－tn = －(x－tn2)，可得 Qn(tn2 + ,0)
所以也有 Qn－1(tn－12 + ,0)，得 tn2－= tn－12 + ，由 tn > 0，得 tn－tn－1 =
∴ tn = t1 + (n－1) = n …………8分
∴ Qn(n(n + 1),0),Qn－1(n(n－1),0)
∴ an = QnQn－1 = n …………10分
(3) 由已知对任意实数时 l∈[0,1] 时 n 2－2n + 2≥(1－l) (2n－1) 恒成立
Û 对任意实数 l∈[0,1] 时，(2n－1)l + n 2－4n + 3≥0 恒成立…………12分
则令 f (l) = (2n－1)l + n 2－4n + 3，则 f (l) 是关于 l 的一次函数.
Û 对任意实数 l∈[0,1] 时
Û …………14分
Û n≥3或n≤1
又 ∵ n∈N *
∴ k 的最小值为3…………16分