高三年级数学综合测试题

高三年级数学综合测试题　

班级　　　　  　　姓名　　　　　 　　学号　　　　　  　　分数　　　　　　  

一、填空题：（每题4分，共48分）

1．  函数的定义域是　　　　 

2．  抛物线与过焦点的直线交于A，B，O是坐标原点，则=　　　　 

3．  已知数列满足，则该数列前26项的和为　　　

4．　如图，直三棱柱ABC—A₁B₁C₁的侧面AA₁B₁B是边长为5的正方形，AB⊥BC，AC与BC₁成60°角，则AC长为　　　　 

5．　以椭圆内的点M（1，1）为中点的弦所在直线方程为　　　　 

6．　函数的图象与y=2^x的图象关于y轴对称，若是的反函数，则的单调递增区间是　　　　 

7．　定义运算x※y=，若m－1※m=m－1，则m的取值范围是　　　　 

8．  某商场开展促销抽奖活动,让参加抽奖的每位顾客从装有编号为0、1、2、3、4、5、6、7、8、9的十个小球的袋子中取球,每次取一个,且取出的小球不再放回袋中.连续取5次,如果取出的5个小球中至少有4个编号为奇数(不计顺序)就可以得奖,则每位抽奖顾客中奖的概率为　　　　　  (用数字作答)

9．  把函数的图象沿x轴向左平移m个单位（m>0），所得函数的图象关于直线对称，则m的最小值为　　　　 

10．=　　　　

11．在函数成等比数列，且，则有最小值，且该值为　　　　　 .

12．设函数(其中)，是的小数点后第位数字，则的值为　　　　 

 二、选择题（每题4分，共16分）

13．已知a、b、c满足c<b<a, ac<0，则下列选项中一定成立的是　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　 B．　　　 C．　　　　　　　D．

14．给出下列四个命题：

　　　 ①“直线a、b为异面直线”的充分非必要条件是“直线a、b不相交”.

　　　 ②“直线l⊥平面α内的所有直线”的充要条件是“l⊥α”.

　　　 ③“直线a⊥b”的充分非必要条件是“a垂直于b在平面α内的射影”.

　　　 ④设α⊥β，，则“a//β”的充分非必要条件是“a⊥α”.

　　其中正确命题的序号是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．①③　　　　　　　　　 B．②③　　　　　　　　　 C．②④　　　　　　　　　 D．②③④

15．命题:，命题:；若是的充分而不必要条件，则的取值范围是：（　　  ）

A．　　　　  B．　　  C．　　　　　　D．

16．等比数列｛a_n｝的公比为，前n项和为满足=，那么a₁的值为（　 ）

A．　　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　 　D．

三、解答题(共86分)

17．（本题满分12分）

已知且，解关于的不等式

18．（本题满分12分）

　　已知函数的周期为

（1）求ω的值；

（2）设△ABC的三边a、b、c满足b²=ac，且边b所对的角为x，求此时函数的值域

19．（本题满分14分）

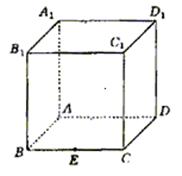
　　如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，点E是棱BC的中点，点F是棱CD上的动点.

（1）试确定点F的位置，使得D₁E⊥平面AB₁F；

（2）当D­₁E⊥平面AB₁F时，求二面角C₁—EF—A的大小（结果用反三角函数值表示）.

20．（本题满分14分）

　　某水库年初的存水量为a（a≥10000），其中污染物的含量为P₀，该年每月降入水库的水

量与月份x的关系是（1≤x≤12，x∈N），且每月流入水库的污水量r，

其中污染物的含量为P（P＜r），又每月库水的蒸发量也为r（假设水与污染物能充分混合，

且污染物不蒸发，该年水库中的水不作它用）.

（1）求第x个月水库含污比g(x)的表达式（含污比）；

（2）当P₀=0时，求水质最差的月份及此月份的含污比.

21．（本题满分16分）

已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点为圆心，1为半径为圆相切，又知C的一个焦点与A关于直线y=x对称.

（1）求双曲线C的方程；

（2）若Q是双曲线C上的任一点，F₁、F₂为双曲线C的左、右两个焦点，从F₁引∠F₁QF₂的平分线的垂线，垂足为N，试求点N的轨迹方程.

（3）设直线y=mx+1与双曲线C的左支交于A、B两点，另一直线L经过M（－2，0）及AB的中点，求直线L在y轴上的截距b的取值范围.

22．（本题满分18分）

已知是定义在上的恒不为零的函数，且对于任意的、都满足：

（1）求的值，并证明对任意的，都有；

（2）设当时，都有，证明在上是减函数；

（3）在（2）的条件下，求集合中的最大元素和最小元素。

高三数学参考答案及评分标准

一、填空题1. 2. 3. －10　4.  5. x+4y－5=0　6. 7. 8. 9.  10.  11. 3　12. 1二、选择题13.C．14.C．15. A．16. D．

三、解答题

17.解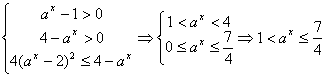：…………6分

若则log…………9分

若则…………12分

18．解：（1） …………3分

由的周期　 ∴…………6分

（2）由题意，得　…………8分

又∵　 ∴　∴ …………10分

∴ …………12分

19．解：解法一：（I）连结A₁B，则A₁B是D₁E在面ABB₁A；内的射影。

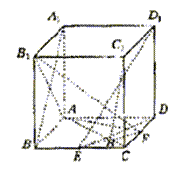　　∵AB₁⊥A₁B，∴D₁E⊥AB₁，…………2分

　　　　于是D₁E⊥平面AB₁FD₁E⊥AF.

　　　 连结DE，则DE是D₁E在底面ABCD内的射影.

　　　　∴D₁E⊥AFDE⊥AF. ………4分

　　　　∵ABCD是正方形，E是BC的中点.

　　　 ∴当且仅当F是CD的中点时，DE⊥AF，即当点F是CD的中点时，D₁E⊥平面AB₁F. …………6分

　　　 （II）当D₁E⊥平面AB₁F时，由（I）知点F是CD的中点.

　　　　又已知点E是BC的中点，连结EF，则EF∥BD. 连结AC，

　　　 设AC与EF交于点H，则CH⊥EF，连结C₁H，则CH是C₁H在底面ABCD内的射影.…………8分

　　　　C₁H⊥EF，即∠C₁HC是二面角C₁—EF—C的平面角. …………10分

　　　　在Rt△C₁CH中，∵C₁C=1，CH=AC=，

　　　　∴tan∠C₁HC=.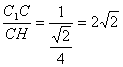

　　　　又因为∠AHC₁=∠C₁HC，故二面角C₁—EF—A的平面角的正切值为。…………14分

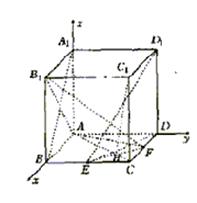
　　　　解法二：以A为坐标原点，建立如图所示的空间直角坐标系。

　　　　（1）设DF=x，则A（0，0，0），B（1，0，0），D（0，1，0），

　　　　A₁（0，0，1），B（1，0，1），D₁（0，1，1），E，F（x，1，0）

　　　　∴。

∴…………4分

于是，。

即，故当F是CD中点时，。…………6分

　　　 （2）当D₁E⊥平面AB₁F时，F是CD的中点，又E是BC的中点，连结EF，则EF∥BD. 连结AC，设AC与EF交于点H，则AH⊥EF. 连结C₁H，则CH是C₁H在底面ABCD内的射影.

　　　　∴C₁H⊥EF，即∠AHC₁是二面角C₁—EF—A的平面角. …………10分

　　　　

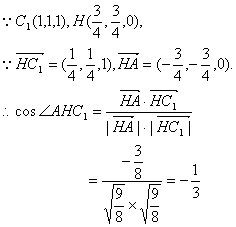
　　　　，即二面角C₁—EF—A的平面角的正切值为。

 …………14分

20．解：（1）第x月水库含污染物P₀+P_x，库容总量=……2分

　  当

　  此时库容量=a+14+15+…+（13+x）= ……4分

　  当

　  此时，库容总量= a+99+20+19+…+（27－x）=　……6分

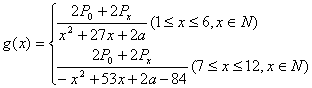　  ∴ …………8分

　  （2）∵P₀=0，a≥10000，当1≤x≤6时，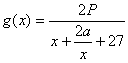

易证上是减函数，且恒大于零，

∴上是增函数　∴当x=6时，……10分

当7≤x≤12时，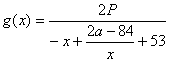

易证在（0，+∞）上是减函数，且恒大于零.

∴上是增函数………12分　　

当x=12时，

∵a≥10000，

∴水质量最差的是12月份，其含污比为　…………14分

21．解：（1）设双曲线C的渐近线方程为y=kx，即kx－y=0

∵该直线与圆 相切，

∴双曲线C的两条渐近线方程为　…………2分

故设双曲线C的方程为，又∵双曲线C的一个焦点为

∴，∴双曲线C的方程为　………4分

（2）若Q在双曲线的右支上，则延长QF₂到T，使QT=OF₁

若Q在双曲线的左支上，则在QF₂上取一点T，使QT=QF₁

根据双曲线的定义TF₂=2，所以点T在以F₂为圆心，2为半径的圆上，即点T的轨迹方程是　① …………8分

由于点N是线段F₁T的中点，设N（x，y），T（）

则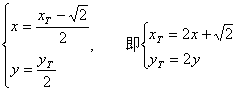

代入①并整理得点N的轨迹方程为  ……10分

（3）由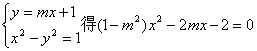

令

直线与双曲线左支交于两点，等价于方程 上有两个不等实根.

因此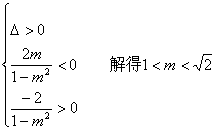　又AB中点为

∴直线L的方程为　…………14分

令x=0，得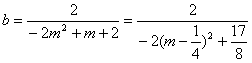

∵　∴　

∴故b的取值范围是　 …………16分

22．解：（1）

　　　 …………4分

　 （2）∵当时，都有…………6分

　　　  ∴当，即时，有，…………8分

　　即

∴在上是减函数。…………10分

（3）∵在上是减函数，{}是递增数列∴数列是递减数列。…………14分

∴集合中的最大元素为，最小元素为 。…………18分