高三年级文科数学第五次月考
数 学（文） 试 题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题）两部分．卷面共150分，考试时间120分钟.
第Ⅰ卷（选择题 共50分）
一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．某学校有老师
人,男学生
人,女学生
人.现用分层抽样的方法从所有师生中抽取一个容量为
的样本.已知从男学生中抽取的人数为
人,则
（ ）
A．
B．
C．
D．
2．已知等差数列
中，
，则该数列前9项和
等于 （ ）
A．
B．
C．
D．
3．实数
是直线
和
平行的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
4．
,且
是第四象限的角,则
（ ）
A．
B．
C．
D．
5．设集合
,
,定义集合
,则
中所有元素之积为
（
）
A．
B．
C．
D．
6．函数
的图象大致是 （ ）
 |
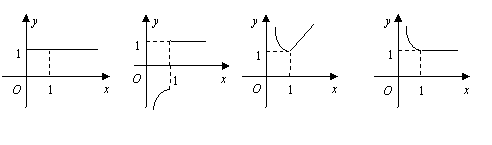A． B． C． D．
7．设两个非零向量
,
,若向量
与
的夹角为锐角,则实数
的取值范围是 （ ）
A．
B．
或
| |
或
或
D．或
8．已知平面
外不共线的三点A，B，C到的距离都相等，则正确的结论是 （ ）
A．平面ABC必平行于
B．平面ABC必与相交
C．平面ABC必不垂直于
D．存在△ABC的一条中位线平行于或在内
9．点
是椭圆
（
上的任意一点，
是椭圆的两个焦点，且∠
，则该椭圆的离心率
的取值范围是 （ ）
A．
B．
C．
D．
10．已知平面上点
，则满足条件的点
在平面上所组成图形的面积是 （ ）
A．
B．
C．
D．
二、填空题：本大题共7小题，每小题4分，共28分.
11．已知函数
，则
．
12．已知
的三边长为三个连续的正整数，且最大角为钝角，则最长边长为 ．
13．在
的展开式中，
的系数为 ．
14．有6个座位连成一排，现有3人就坐，则恰有两个空座位相邻的不同坐法有 种．
15．甲、乙、丙3人投篮，投进的概率分别是 ，， ．现3人各投篮1次，则3人中恰有2人投进的概率是 ．
16．已知数列的前项和
满足关系式
，则的通项公式是 ．
17．已知半球
的半径为
,它的内接长方体
的一个面
在半球的底面上,则该长方体的体积最大值为 ．
三、解答题
18．（本小题满分14分）
已知函数
．
（1）若
，求
的单调递增区间；
（2）若
时，的最大值为4，求
的值，并指出这时的值．
| |
19．（本小题满分14分）
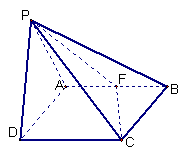
如图，四棱锥
，面
⊥面，△是等边三角形，底面 是矩形，
，
是
的中点．
（1）求证：
；
（2）求
与平面所成的角；
（3）求二面角
的度数。
20．(本小题满分14分)
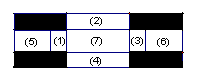
将一张2
6米的硬钢板按图纸的要求进行操作，沿线裁去阴影部分，把剩余部分按要求焊接成一个有盖的长方体水箱（其中①与③、②与④分别是全等的矩形，且⑤+⑥=⑦），设水箱的高为米，容积为
立方米。（1）求关于的函数关系式；（2）如何设计的大小，使得水箱装的水最多？
21．（本小题满分14分）
已知数列{
}中
，
（
），
数列
满足:
（
）
（1）求证:数列
是等差数列；
（2）求数列中的最大项与最小项，并说明理由.
22．（本小题满分16分）
已知为坐标原点，点
的坐标分别为
,动点满足：
（1）求动点的轨迹
的方程；
（2）过
点做直线与相交于
两点，且
，求直线MN的方程。
参考答案
一．选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | C | A | C | D | C | D | A | B |
二．填空题：
11． 
12． 
13．
14．
15.
16.
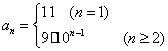17.
三．解答题：
18．解：（1）
．
解不等式
．
得
∴f（x）的单调增区间为
，
．
（2）∵
，
]，∴
．
∴当
即
时，
．
∵3＋a＝4，∴a＝1，此时．
19．解：取AD的中点G，连结PG，CG．
|
（1）∵△ADP为正三角形，∴PG⊥AD．
又面PAD⊥面ABCD．AD为交线，
∴PG⊥面ABCD，∴PG⊥CD，又AD⊥CD
∴CD⊥面PAD，∴
（2）由（1）∴PG⊥面ABCD，则∠PCG为PC与
平面ABCD所成的角．
设AD＝a，则
，
．
在Rt△GDC中，
．
在Rt△VGC中，
．
∴
．
即VC与平面ABCD成30°．
（3）连结GF，则
．
而
．
在△GFC中，
．∴GF⊥FC．
连结PF，由PG⊥平面ABCD知PF⊥FC，则∠PFG即为二面角P-FC-D的平面角．
在Rt△VFG中，
．
∴ ∠VPG＝45°．二面角P-FC-B的度数为135°．
20．解：（1）设水箱的高为（米），则水箱底面（7）
长宽分别为
（米），
（米）
故水箱的容积为
（2）由
，得：
所以：
在
上单调递增，在
上单调递减
所以
时水箱的容积最大。
21．解：（1）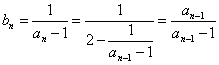
，
而
，
∴
．
∴{
}是首项为
，公差为1的等差数列．
（2）依题意有
，而
，
∴
．
函数
，在（3.5，
）上为减函数．在（
，3.5）上也为减函数．
故当n＝4时，
取最大值3，n＝3时，取最小值-1．
22．解：（1）∵
由椭圆的第一定义可知点P的轨迹为椭圆，
且2a＝4，c＝1，∴
∴所求的椭圆方程为
（2）①当直线MN的斜率不存在时，不满足题意；
②当直线MN的斜率存在时，设其方程为
，
代入
化简得
设两交点的坐标为M（
）、N（
）
则
∵
，∴
，
∴
∴
∴所求的直线MN的方程为