高三年级文科数学调研考试
数学(文科)
说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答题时间120分钟,满分150分.
第Ⅰ卷(选择题,共60分)
注意事项:
1.答第一卷前,考生务必用蓝、黑墨水或圆珠笔将姓名、考试证号、填在答题卡上,并用2B铅笔在答题卡规定位置涂黑自己的考试证号和考试科目.
2.每小题选出答案后,用铅笔涂黑答题卡上对应题目的答案标号.如需改动,用橡皮擦干净后,再选涂其它答案标号.答案写在试卷上无效.
一、选择题(本大题共12小题,每小题5 分,共60分.在第小题给出的四个选项中,只有一项是符合题目要求的)
1.集合![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() 的值是 ( )
的值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.要得到函数![]() 的图象,可将函数
的图象,可将函数![]() 的图象沿x轴 ( )
的图象沿x轴 ( )
A.向左平移![]() 单位 B.向右平移
单位 B.向右平移![]() 单位
单位
C.向左平移![]() 单位 D.向右平移
单位 D.向右平移![]() 单位
单位
4.函数![]() 的反函数为 ( )
的反函数为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.![]() ,则下列不等式正确的个数是 ( )
,则下列不等式正确的个数是 ( )
①![]() ②
②![]() ③
③![]() ④
④![]()
A.1个 B.2个 C.3个 D.4个
6.过点(1,1)的直线l与圆![]() 相交于A、B两点,当弦AB的长度最小时,直线l的斜率为 ( )
相交于A、B两点,当弦AB的长度最小时,直线l的斜率为 ( )
A.2 B.-1 C.-2 D.1
7.等差数列![]() 的值为 ( )
的值为 ( )
A.20 B.-20 C.10 D.-10
|
A.(-1,0) B.(0,1)
C.![]() D.
D.![]()
9.设a,b,c是△ABC的三条边,若a,b,c成等比数列,且c=2a,则cosB等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知△ABC中,向量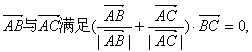 且
且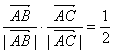 ,则△ABC为 ( )
,则△ABC为 ( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.已知奇函数![]() 的定义域为R,且是以2为周期的周期函数,数列
的定义域为R,且是以2为周期的周期函数,数列![]() 是首项为1,公差为1的等差数列,则
是首项为1,公差为1的等差数列,则![]() 的值为 ( )
的值为 ( )
A.0 B.1 C.-1 D.2
第Ⅱ卷(非选择题,共90分)
注意事项:
1.用钢笔或圆珠笔直接答在试题卷中.
2.答卷前将密封线内项目填写清楚.
二、填空题(本大题共4小数点题,每小题4分,共16分.把答案填在题中横线上)
13.不等式![]() 的解集为
.
的解集为
.
14.若![]() 则向量a与b的夹角为
.
则向量a与b的夹角为
.
15.已知![]() =
.
=
.
16.定义“等积数列”:在一个数列中,如果每一项与它后一项的积都为同一常数,那么这个数列叫做“等积数列”,这个常数叫做该数列的公积。已知数列![]() 是等积数列,且
是等积数列,且![]() 公积为5,则这个数列的前21项的和S21的值为
。
公积为5,则这个数列的前21项的和S21的值为
。
三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程式演算步骤)
17.(本小题满分12分)
已知函数![]()
(Ⅰ)求![]() 的最小正周期;
的最小正周期;
(Ⅱ)求![]() 的单调弟增区间.
的单调弟增区间.
18.(本小题满分12分)
已知关于x的不等式![]() 在区间[1,2]上恒成立,求实数a的取值范围。
在区间[1,2]上恒成立,求实数a的取值范围。
| |
19.(本小题满分12分)
已知数列![]() 的前n项为Sn,且当
的前n项为Sn,且当![]() 时满足
时满足![]() 数列
数列![]() 满足
满足![]() 数列
数列![]() 满足
满足![]()
(Ⅰ)求数列![]() 的通项公式
的通项公式![]() ;
;
(Ⅱ)求数列![]() 的前n项和Tn.
的前n项和Tn.
20.(本小题满分12分)
如果![]() 在某个区间I内满足:
在某个区间I内满足:
对任意的![]() ,则称
,则称![]() 在I上为下凸函数;已知函数
在I上为下凸函数;已知函数![]()
(Ⅰ)证明:当![]() 时,
时,![]() 在R上为下凸函数;
在R上为下凸函数;
(Ⅱ)若![]() 时,
时,![]() 求实数a的取值范围.
求实数a的取值范围.
| |
21.(本小题满分14分)
已知点A、B是抛物线![]() 上的两个不同于坐标原点O的动点,且
上的两个不同于坐标原点O的动点,且![]()
(Ⅰ)求以AB为直径的圆的圆心轨迹方程;
(Ⅱ)过A、B分别作抛物线的切线,证明:两切线交点M的纵坐标为定值.
22.(本上题满分12分)
已知函数![]() 在区间
在区间![]() 上单调递增,在区间[-2,2]上单调递减,且
上单调递增,在区间[-2,2]上单调递减,且![]()
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设![]() ,若对任意的x1、x2
,若对任意的x1、x2![]() 不等式
不等式![]() 恒成立,求实数m的最小值。
恒成立,求实数m的最小值。
参 考 答 案
一、选择题(本大题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | D | C | C | A | D | A | B | C | A | A |
二、填空题(本大题共4小题,每小题4分,共16分)
13.![]()
14.![]()
15.![]()
16.47
三、解答题(本大题共6小题,共74分)
17.(本小题满分12分)
解(Ⅰ)![]()
![]() ………………………………………………………4分
………………………………………………………4分
![]() 的最小正周期为
的最小正周期为![]() .………………………………………………6分
.………………………………………………6分
(Ⅱ)由![]() ,…………………………………………8分
,…………………………………………8分
得![]() …………………………………………10分
…………………………………………10分
![]() 的单调增区间为
的单调增区间为![]() ……………………12分
……………………12分
18.(本小题满分12分)
解当![]()
![]() ………………………………………………………………3分
………………………………………………………………3分
根据条件,a应小于![]() 的最小值是
的最小值是![]() ,
,
![]() …………………………………………………………………………6分
…………………………………………………………………………6分
当![]() 时,
时,![]()
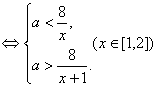 …………………………………………………………9分
…………………………………………………………9分
根据条件,a应小于![]() 的最小值4;
的最小值4;
同时a应大于![]()
![]() 的最大值4,即
的最大值4,即![]() ,不成立。……11分
,不成立。……11分
综上,a的取值范围是![]() …………………………………………………………12分
…………………………………………………………12分
19.(本小题满分12分)
解(Ⅰ)当![]() ……………………………………………………2分
……………………………………………………2分
当![]() ………………………………………………4分
………………………………………………4分
![]() ………………………………………………………………………6分
………………………………………………………………………6分
(Ⅱ)![]()
![]() ………………………………8分
………………………………8分
![]()
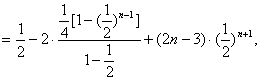 …………………………10分
…………………………10分
![]() ………………………………………………………12分
………………………………………………………12分
20.(本小题满分12分)
解(Ⅰ)![]()
![]()
![]() ………………………………………………………………4分
………………………………………………………………4分
![]()
![]() 为R上的下凸函数。………………………………6分
为R上的下凸函数。………………………………6分
(Ⅱ)![]()
![]()
![]() ………………………………………………10分
………………………………………………10分
![]()
![]() ………………………………………………………………12分
………………………………………………………………12分
21.(本小题满分14分)
解(Ⅰ)设![]() …………………………1分
…………………………1分
![]()
![]() …………………………………………………………………3分
…………………………………………………………………3分
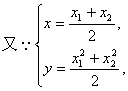 …………………………………………………………5分
…………………………………………………………5分
则![]() ]
]
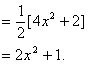
![]() 为直径的圆的圆心的轨迹方程为
为直径的圆的圆心的轨迹方程为![]() …………………………7分
…………………………7分
(Ⅱ)由![]() ,得
,得![]() ,……………………………………………………9分
,……………………………………………………9分
∴过A点的切线方程为![]() ,即
,即![]() ①
①
同理过B点的切线方程为![]() ②……………………………………12分
②……………………………………12分
设![]()
则![]() 的两根,
的两根,
由韦达定理知![]() 又由(Ⅰ)
又由(Ⅰ)![]()
![]() …………………………………………14分
…………………………………………14分
22.(本小题满分12分)
解(Ⅰ)![]()
![]() 上单调递增,在[-2,2]上单调递减
上单调递增,在[-2,2]上单调递减
![]() ,……2分
,……2分
![]() ,
,
![]() …………………………4分
…………………………4分
又![]()
![]()
![]() ……………………………………………………6分
……………………………………………………6分
(Ⅱ)已知条件等价于在![]() ……………………8分
……………………8分
![]() 上为减函数,
上为减函数,
且![]() ……………………………………10分
……………………………………10分
![]() 上为减函数,
上为减函数,
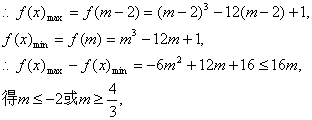
又![]() ………………………………………………12分
………………………………………………12分