高三年级第一学期期末检测数学试卷
| 题号 | 一 | 二 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
| 得分 |
注意：1.答卷前，考生务必将学校、班级、姓名、学号等填写清楚.
|
与
表示意义相同.
3.本试卷共有22道试题，满分150分.考试时间120分钟.
一. 填空题（本大题满分48分）本大题共有12题，只要求直接
填写结果，每题4分.
1.等差数列
的首项
，
，则的公差d=
.
2. 若在同一坐标系内函数
的图像关于直线y=x对称，则
.
3. 已知函数
（x∈R）的最小正周期为p ，则w = .
4. 若
，则
.（用反三角函数表示）
5. 袋中有3只白球和a只黑球，从中任取2只，恰好一白一黑的概率为
，则a= .
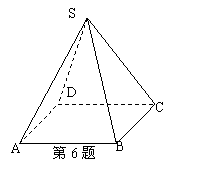
6. 如图，正四棱锥
的侧棱长是底面边长的2倍，则异面直线
所成角的大小是
（用反三角函数表示）.
7.(理)
.
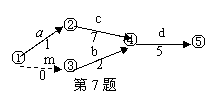
（文）某工程的工序流程图如图所示（工时数单位：天），则工程总时数为 _____天.
8. 在△
中，若
，
，则
.
9. 在rABC中，a、b、c 分别为ÐA、ÐB、ÐC的对边，ÐA=60°，b=1，c=4，则
.
10. 已知函数
的定义域为
，则实数p的取值范围是 .
11. 心脏跳动时，血压在增加或减小.血压的最大值、最小值分别称为收缩压和舒张压，血压计上的读数就是收缩压和舒张压，读数120/80mmHg为标准值.设某人的血压满足函数式
，其中
为血压（mmHg），t为时间（min）.此人的血压在血压计上的读数为 （mmHg）.
12. 对于正整数n定义一种满足下列性质的运算“*”：（1）1*1=2；（2）（n+1）*1=n*1+2n+1.则用含n的代数式表示n*1= .
|
四个结论，其中有且只有一个结论是正确的，必须把正确结论的
代号写在题后的圆括号内，选对得 4分，否则一律得零分.
13. 
的直角边
在平面
内，顶点
在平面外，则直角边
、斜边
在上的射影与直角边组成的图形可以是（ ）.
（A）线段或锐角三角形 （B）线段或直角三角形 （C）线段或钝角三角形 （D）线段、锐角三角形、直角三角形或钝角三角形.
14. 若函数y=f(x) (xÎR)满足f(x+2)=f(x)，且xÎ(－1,1]时，f(x)=x．则函数y=f(x)的图象与函数y=log4x的图象的交点的个数为（ ）.
（A）3 （B）4 （C）6 （D）8.
15. 已知
，且向量
与
平行，则下列说法正确的是（ ）.
（A）
，向量与方向相反 （B），向量与方向相同 （C）
，向量与方向相反 （D），向量与方向相同.
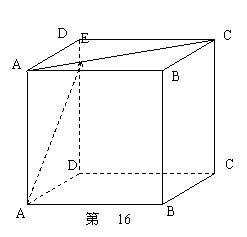16. （理）在正方体
中，点E在A1C1上，
且
，则（ ）.
（A）
，（B）
，（C）
，（D）
.
（文）变量x、y满足下列条件：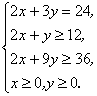
则使
的值最小的
是（ ）.
（A）（9，2） （B）（6，4） （C）（4.5，3） （D）（3，6）.
三．解答题（本大题满分86分）本大题共有6题，解答下列各题必须写出必要的步骤.
17. (本题满分12分) 本题共有2个小题，每1小题满分6分. 已知集合
，
.
（1）用区间表示集合
；
（2）求
.
[解] （1） （2）
18. (本题满分12分) 本题共有2个小题，每1小题满分6分.
已知
，其中i为虚数单位，
.
（1）求
的取值范围；
（2）如果
和
互为共轭复数，求q.
[解]（1）
19. (本题满分14分) 本题共有2个小题，第1小题满分6分，
第2小题满分8分.
已知正方体
的棱长为2，点E、F分别在底面正方形的边AB、BC上，且
，点G为棱
的中点.
（1） 
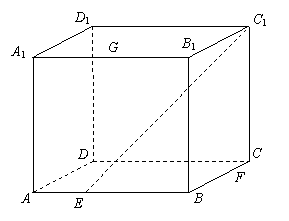在图中画出正方体过三点E、F、G的截面，并保留作图痕迹；
（2） （理）求（1）中的截面与底面ABCD所成锐二面角的大小.
（文）求出直线EC1与底面ABCD所成角的大小.
[解]（1）
（2
20. (本题满分14分)本题共有2个小题，第1小题满分6分， 第2小题满分8分.
已知两个向量
，
.
（1）若t=1且
，求实数x的值；
（2）对tÎR写出函数
具备的性质.
[解]（1）
21. (本题满分16分)本题理科同学共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分.文科同学共两个小题，第1小题满分6分，第2小题满分10分.
为了保护一件珍贵文物，博物馆需要在一种无色玻璃的密封保护罩内充入保护气体.假设博物馆需要支付的总费用由两部分组成：罩内该种气体的体积比保护罩的容积少0.5立方米，且每立方米气体费用1千元；‚需支付一定的保险费用，且支付的保险费用与保护罩容积成反比，当容积为2立方米时，支付的保险费用为8千元.
（1） 求博物馆支付总费用y与保护罩容积V之间的函数关系式；
（2）求博物馆支付总费用的最小值；
（3）（理）如果要求保护罩可以选择正四棱锥或者正四棱柱形状，且保护罩底面（不计厚度）正方形边长不得少于1.1米，高规定为2米. 当博物馆需支付的总费用不超过8千元时，求保护罩底面积的最小值（结果保留一位小数）.
[解]（
22. (本题满分18分)本题共有3个小题，第1小题满分4分， 第2小题满分6分. 第3小题满分8分.
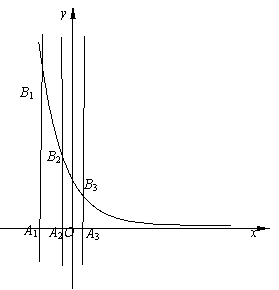已知等差数列
的首项为
，公差为
.对于不同的自然数n，直线
与x轴和指数函数
的图像分别交于点
（如图所示），记
的坐标为
，直角梯形
、
的面积分别为
和
，一般地记直角梯形
的面积为
.
（1） 求证数列
是公比绝对值小于1的等比数列；
（2） 设的公差
，是否存在这样的正整数n，构成以
为边长的三角形？并请说明理由；
（3） （理）设的公差为已知常数，是否存在这样的实数p使得（1）中无穷等比数列各项的和S>2010？并请说明理由.
（文）设的公差
，是否存在这样的实数p使得（1）中无穷等比数列各项的和S>2010？如果存在，给出一个符合条件的p值；如果不存在，请说明理由.
[证明]（1）
静安区2005高三第一学期期末检测参考解答与评分标准
一、填空（每小题4分）
1．3； 2．
； 3．1； 4．
5．a=4； 6． 
，
等 7．理
；文13； 8． -16
9． 
； 10．
； 11．135/85（mmHg）；
12．n*1=2n+1-2。
二、选择题（每小题4分） 13~16 B C A D
三、解答题
17．解：（1）
，所以
……6分
（2）
……12分
18．（1）
，
……2分
当
时， 
取最小值1，当
时， 取最大值
……4分
所以取值范围为
……6分
（2）
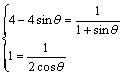……8分
所以
……10分
……12分
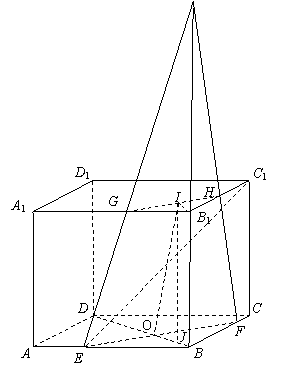
19．（1）如图，截面为EFHG ……6分
（2）（理）解法1：连接BD交EF于O点，连接B1D1交GH于I点，在平面BOIB1过I点作BO的垂线，垂足为J。在RT△IJO中，由二面角定义ÐIOJ为所求的角设为a ……9分
在RT△IJO中，OJ=
，
，
……12分
截面EFHG与底面所成锐二面角大小为
……14分
（通过三垂线定理加以说明也可）
解法2：如图，建空间直角坐标系，
，
，
，
……8分
平面EFHG法向量为（-6，-6，1），底面法向量为（0，0，1） ……10分
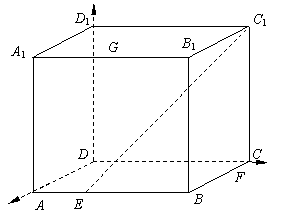设向量夹角q，
……12分
截面EFHG与底面所成锐二面角大小为
…………………14分
文：ÐC1EC就是所求的角 ……9分
在RT△C1CE中，
，
……12分
所以直线EC1与底面所成角大小为
……14分
20．解：（1）由已知得
……2分
……4分
解得
，或
……6分
（2）
……8分
具备的性质：
①偶函数；
②当
即
时，
取得最小值
（写出值域为
也可）；
③单调性：在
上递减，
上递增；由对称性，在
上递增，在
递减
……14分
说明：写出一个性质得3分，写出两个性质得5分，写出三个性质得6分，包括写出函数的零点（，
）等皆可。写出函数的定义域不得分，写错扣1分
21．：（1）
（或
）（
）
……（理4分，文6分）
（2）
……（理8分，文12分）
当且仅当
，即V=4立方米时不等式取得等号……（理10分，文15分）
所以，博物馆支付总费用的最小值为7500元。 ……（文16分）
（3）（理）解法1：由题意得不等式：
……（理12分）
当保护罩为正四棱锥形状时，
，代入整理得：
，解得
；
当保护罩为正四棱柱形状时，
，代入整理得：
，解得
……（理15分）
又底面正方形面积最小不得少于
，所以，底面正方形的面积最小可取1.4平方米
………（理16分
解法2. 解方程
，即
得两个根为
……（理12分）
由于函数
在
上递减，在
上递增，所以当
时，总费用超过8000元，所以V取得最小值
……（理14分）
由于保护罩的高固定为2米，所以对于相等体积的正四棱锥与正四棱柱，正四棱柱的底面积是正四棱锥底面积的
。所以当保护罩为正四棱柱时，保护罩底面积最小，
m2
……（理15分）
又底面正方形面积最小不得少于，
，所以，底面正方形的面积最小可取1.4平方米
……（理16分）
解法3. 解
……（理12分）
得
……（理14分）
又底面正方形面积最小不得少于，当保护罩为正四棱锥形状时，
；当保护罩为正四棱柱形状时，
。所以，保护罩容积可取最小
立方米，当形状为棱柱时底面正方形的面积最小，为1.4平方米 ……（理16分）
22．（1）
，
……2分
，对于任意自然数n，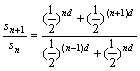
=
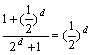，所以数列是等比数列且公比
，因为
，所以
……4分
（写成
，得公比
也可）
（2）
，
，对每个正整数n，
……6分
若以为边长能构成一个三角形，则
，即
，1+2>4，这是不可能的
……9分
所以对每一个正整数n，以为边长不能构成三角形
……10分
（3）（理）由（1）知，
，
……11分
所以
……14分
若
……16分
两边取对数，知只要
取值为小于
的实数，就有S>2010……18分
说明：如果分别给出
与d的具体值，说明清楚问题，也参照前面的评分标准酌情给分，但不得超过该部分分值的一半。
（文）
，
……11分
所以
……14分
如果存在p使得
，即
……16分
两边取对数得：
，
因此符合条件的p值存在，
，可取p= -11等 ……18分
说明：通过具体的p值，验证也可。