08届高三数学第二次教学质量统一检测
试题(理科)
命题、审题: 贺功保(市教科院) 张耀华(株洲市二中) 方厚良(株洲县五中)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
参考公式: http://www.mathedu.cn
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
![]()
![]()
如果事件A、B相互独立,那么 其中,c表示底面周长、l表示斜高或
![]() 母线长
母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P,那么n次独立重复实验中恰好发生k
![]()
次的概率![]() 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.答案要写在答题卷上。
1、不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2、函数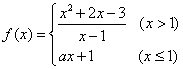 在点
在点![]() 处连续,则
处连续,则![]() 的值是 ( )
的值是 ( )
A.2 B. ![]() C.3
D.
C.3
D. ![]()
3、已知在![]() 中,
中,![]() ,S△ABC =
,S△ABC =![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
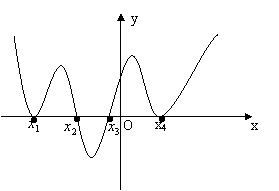 4、已知函数
4、已知函数![]() 的导函数
的导函数![]() 的图像如下,则
( )
的图像如下,则
( )
A.函数![]() 有1个极大值点,1个极小值点
有1个极大值点,1个极小值点
B.函数![]() 有2个极大值点,2个极小值点
有2个极大值点,2个极小值点
C.函数![]() 有3个极大值点,1个极小值点
有3个极大值点,1个极小值点
D.函数![]() 有1个极大值点,3个极小值点
有1个极大值点,3个极小值点
5、已知二面角![]() ,直线
,直线![]() ,
,![]() ,且a与l不垂直,b与l不垂直,那么( )
,且a与l不垂直,b与l不垂直,那么( )
A.a与b可能垂直,但不可能平行 B.a与b可能垂直,也可能平行
C.a与b不可能垂直,但可能平行 D.a与b不可能垂直,也不可能平行
6、已知数列{an}满足a1=0,an+1=( n∈N*),则a2007= ( )
A.0 B.- C. D.
7、以平行六面体![]() 的任意三个顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率是( )
的任意三个顶点作三角形,从中随机取出两个三角形,则这两个三角形不共面的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
8、已知双曲线![]() 的焦点为
的焦点为![]() 、
、![]() ,
,![]() 为双曲线上一点,以
为双曲线上一点,以![]()
![]() 为直径的圆与双曲线的一个交点为
为直径的圆与双曲线的一个交点为![]() ,且
,且![]() ,则双曲线的离心率为 ( )
,则双曲线的离心率为 ( )
A.![]() B.
B.![]() C.2
D.
C.2
D.![]()
9、已知三棱锥![]() —
—![]() 的四个顶点均在半径为1的球面上,且满足
的四个顶点均在半径为1的球面上,且满足![]() ,
,![]() ,
,![]() ,则三棱锥
,则三棱锥![]() —
—![]() 的侧面积的最大值为 ( )
的侧面积的最大值为 ( )
A.2
B.1 C.![]() D.
D.![]()
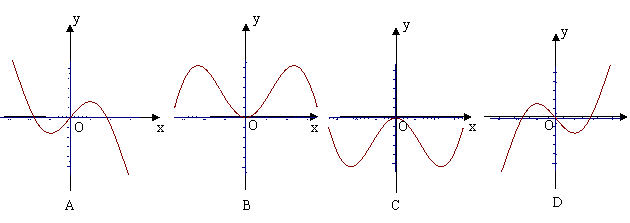 10、设函数
10、设函数![]() 的图象上的点
的图象上的点![]() 的切线的斜率为
的切线的斜率为![]() ,若
,若![]() ,则函数
,则函数![]() ,
,![]() 的图象大致为
( )
的图象大致为
( )
第Ⅱ卷(非选择题)
二、填空题:本大题共5小题,每小题5分 ,共25分,把答案填在答题卡中对应题号后的横线上.
11、直线![]() 交抛物线
交抛物线![]() 于M(x1,y1),N(x2,y2),且
于M(x1,y1),N(x2,y2),且 ![]() 过焦点,则
过焦点,则![]() 的值为
.
的值为
.
12、若![]() ,且
,且![]() ,则实数
,则实数![]() 的值为 __________.
的值为 __________.
13、函数![]() 的单调递增区间是
.
的单调递增区间是
.
14、在直角坐标平面上,不等式组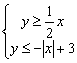 所表示的区域的面积为 .
所表示的区域的面积为 .
15、若钝角三角形三内角的度数成等差数列,且最小边长与最大边长的比值为m,则m的取值范围是 .
三.解答题:本大题共6小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16、(本小题满分12分)已知![]() 中,
中,![]() 、
、![]() 、
、![]() 是三个内角
是三个内角![]() 、
、![]() 、
、![]() 的对边,关于
的对边,关于![]() 的不等式
的不等式![]() 的解集是空集.
的解集是空集.
(1)求角![]() 的最大值;
的最大值;
(2)若![]() ,
,![]() 的面积
的面积![]() ,求当角
,求当角![]() 取最大值时
取最大值时![]() 的值.
的值.
17、(本小题满分12分)袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中有放回地摸球,每次摸出一个,有3次摸到红球即停止.
① 求恰好摸5次停止的概率;
② 记5次之内(含5次)摸到红球的次数为ξ,求随机变量ξ的分布率及数学期望E![]() .
.
(2)若A、B两个袋子中的球数之比为1∶2,将A、B中的球装在一起后,从中摸出一个红球的概率是![]() ,求p的值.
,求p的值.
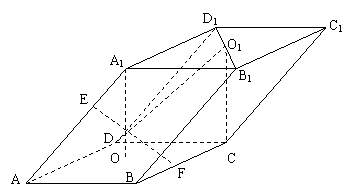
18、(本小题满分12分) 如图,已知平行六面体![]() 的底面为正方形,
的底面为正方形,![]() 分别为上、下底面中心,且
分别为上、下底面中心,且![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,
,
(1)求证:平面![]() 平面
平面![]() ;
;
 (2)若点
(2)若点![]() 、
、![]() 分别在棱
分别在棱![]() 、
、![]() 上,且
上,且![]() ,问点
,问点![]() 在何处时,
在何处时,![]() ?
?
(3)若![]() ,求二面角
,求二面角![]() 的大小.
的大小.
19、(本题满分12分) 假设A型进口车关税税率在2002年是100%,在2007年是25%,2002年A型进口车每辆价格为64万元(其中含32万元关税税款).
(1)已知与A型车性能相近的B型国产车,2002年每辆价格为46万元,若A型车的价格只受关税降低的影响,为了保证2007年B型车的价格不高于A型车价格的90%,B型车价格要逐年降低,问平均每年至少下降多少万元?
(2)某人在2002年将33万元存入银行,假设银行扣利息税后的年利率为1.8%(5年内不变),且每年按复利计算(上一年的利息计入第二年的本金),那么5年到期时这笔钱连本带息是否一定够买按(1)中所述降价后的B型车一辆?
20、(本小题共13分)已知椭圆![]() 的左焦点为F,O为坐标原点。过点F的直线
的左焦点为F,O为坐标原点。过点F的直线![]() 交椭圆于A、B两点.
交椭圆于A、B两点.
(1)若直线![]() 的倾斜角
的倾斜角![]() ,求
,求![]() ;
;
(2)求弦AB的中点M的轨迹;
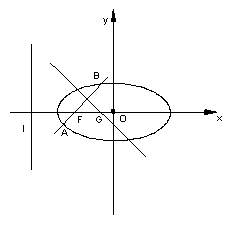 (3)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与
(3)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分线与![]() 轴交于点G,求点G横坐标的取值范围.
轴交于点G,求点G横坐标的取值范围.
21、(本小题满分14分)已知函数![]() 的定义域为
的定义域为![]() ,且同时满足:对任意
,且同时满足:对任意![]() ,总有
,总有![]() ,
,![]() ; 若
; 若![]() ,
,![]() 且
且![]() ,则有
,则有![]() .
.
(1)求![]() 的值;
的值;
(2)试求![]() 的最大值;
的最大值;
(3)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,
求证:![]() .
.
08届高三数学第二次教学质量统一检测
数学参考答案(理科)
命题、审题: 贺功保(市教科院) 张耀华(株洲市二中) 方厚良(株洲县五中)
第Ⅰ卷(选择题)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.答案要写在答题卷上。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | C | A | B | C | C | D | A | A |
第Ⅱ卷(非选择题)
二、填空题:本大题共5小题,每小题5分 ,共25分,把答案填在答题卡中对应题号后的横线上.
11、![]() 12、
12、![]() 13、
13、 ![]()
14、![]() 15、
15、 ![]()
三.解答题:本大题共6小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16、解析: (1)显然![]() 不合题意, 则有
不合题意, 则有![]() ,
,
即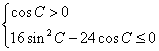 , 即
, 即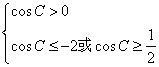 ,
,
故![]() ,∴角
,∴角![]() 的最大值为
的最大值为![]() 。
…………………6分
。
…………………6分
(2)当![]() =
=![]() 时,
时,![]() ,∴
,∴![]() ,
,
由余弦定理得![]() ,
,
∴![]() ,∴
,∴![]() 。
…………………12分
。
…………………12分
17、解析:(1)(i)P=![]() …………………3分
…………………3分
(ii)随机变量![]() 的取值为0, 1, 2, 3.
的取值为0, 1, 2, 3.
由n次独立重复试验概率公式![]() 得
得
![]()
![]()
![]()
![]() … 6分
… 6分
随机变量![]() 的分布列是
的分布列是
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
![]() 的数学期望是
的数学期望是 ![]() ……………8分
……………8分
(2) 设袋子A有m个球,则袋子B中有2m个球.
由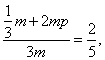 得
得![]() ……………………12分
……………………12分
18、解法一:(1)证明: 建立空间直角坐标系如图所示,设地面正方形的边长为a,![]() ,
,
则 ![]() ,
,
由 ![]() ,得
,得 ![]()
![]()
![]()
![]() 平面
平面![]()
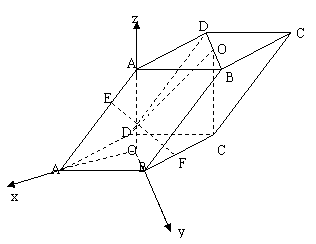 又
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() 平面
平面![]() …………………4分
…………………4分
(2)
由(1)及![]() ,
,
得 ![]()
设![]() ,则
,则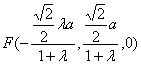 ,
,
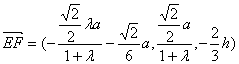
![]()
由![]()
![]()
![]()
![]() …………… 8分
…………… 8分
(3)由![]() ,
,![]() 从而
从而 ![]() ,
,![]()
设 ![]() 是平面
是平面![]() 的一个法向量, 则
的一个法向量, 则 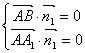
![]()
又 平面![]() 的一个法向量为
的一个法向量为![]()
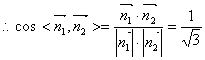
![]() 所求二面角的大小为
所求二面角的大小为![]() ………12分
………12分
解法二:用欧氏几何推证的方法也可以解决。(略)
19、解:(1)2007年A型车价为32+32×25%=40(万元)
设B型车每年下降d万元,2002,2003……2007年B型车价格为:(公差为-d)
![]() ,
,![]() ……
……![]() ∴
∴ ![]() ≤40×90% ∴ 46-5d≤36 d≥2
故每年至少下降2万元…………6分
≤40×90% ∴ 46-5d≤36 d≥2
故每年至少下降2万元…………6分
(2)2007年到期时共有钱![]() >33(1+0.09+0.00324+……)=36.07692>36(万元)
>33(1+0.09+0.00324+……)=36.07692>36(万元)
故5年到期后这笔钱够买一辆降价后的B型车 …………………12分
20、解:(1)直线![]() 方程为
方程为![]() 与
与![]() 联立得
联立得
![]() …………………4分
…………………4分
(2)设弦AB的中点M的坐标为![]() 依题意有
依题意有
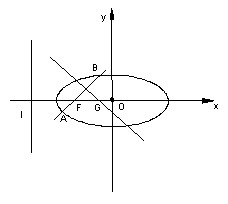
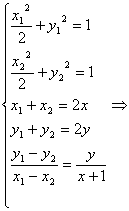
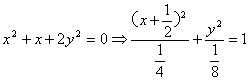
所以弦AB的中点M的轨迹是以![]() 为中心,焦点在
为中心,焦点在![]() 轴上,长轴长为1,短轴长为
轴上,长轴长为1,短轴长为![]() 的椭圆。
…………………8分
的椭圆。
…………………8分
(3)设直线AB的方程为![]()
代入![]() 整理得
整理得![]()
![]() 直线AB过椭圆的左焦点F,
直线AB过椭圆的左焦点F,![]() 方程有两个不等实根。
方程有两个不等实根。
记![]() 中点
中点![]() 则
则![]()
![]() 的垂直平分线NG的方程为
的垂直平分线NG的方程为![]() 令
令![]() 得
得
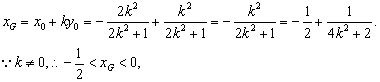
![]() 点G横坐标的取值范围为
点G横坐标的取值范围为![]() …………………13分
…………………13分
21、解:(1)令![]() ,则
,则![]() ,又由题意,有
,又由题意,有![]()
![]() …………………3分
…………………3分
(2)任取 且![]() ,则0<
,则0<![]()
![]()
![]()
![]() 的最大值为
的最大值为![]() …………………6分
…………………6分
(3)由![]()
![]()
又由![]()
![]()
![]() 数列
数列![]() 为首项为1,公比为
为首项为1,公比为![]() 的等比数列,
的等比数列, ![]() …………………8分
…………………8分
当![]() 时,
时,![]() ,不等式成立,
,不等式成立,
当![]() 时,
时,![]()
![]() ,
, ![]()
![]() 不等式成立
不等式成立
假设![]() 时,不等式成立。
时,不等式成立。
即 ![]()
则 当![]() 时,
时,![]()
![]()
![]()
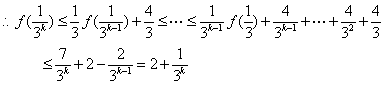
![]()
![]()
即 ![]() 时,不等式成立
时,不等式成立
故 对![]() ,原不等式成立。
…………………14分
,原不等式成立。
…………………14分