08届高三数学第五次调研考试
数学(文科)试卷
一、填空题(本大题共14小题,每小题5分,满分70分,把正确答案写在题中的横线上)
1.已知直线的斜率是-1,则它的倾斜角是 ▲ .
2.已知集合![]() ,则
,则![]() 中元素的个数是▲ .
中元素的个数是▲ .
3.若复数![]() 是纯虚数,则实数 a的值是▲
.
是纯虚数,则实数 a的值是▲
.
4.已知向量![]() 若
若![]() ∥
∥![]() ,则x= ▲ .
,则x= ▲ .
5.抛物线的焦点是曲线![]() 的对称中心,顶点为坐标原点,则此抛物线的方程是 ▲ .
的对称中心,顶点为坐标原点,则此抛物线的方程是 ▲ .
6.利用简单随机抽样的方法,从n个个体(n>13)中逐个抽取13个个体,若第二次抽取时,余下的每个个体被抽取到的概率是![]() ,则在整个抽样过程中,每个个体被抽到的概率是
,则在整个抽样过程中,每个个体被抽到的概率是
▲ .
7.函数![]() 在区间
在区间![]() 上是减函数,则a的取值范围是▲.
上是减函数,则a的取值范围是▲.
8.若椭圆![]() 的离心率是
的离心率是![]() ,则k的值是 ▲ .
,则k的值是 ▲ .
 9.在算式30-△=4×□中的△、□分别填入一个正数,使它们的倒数和最小,则这两个数构成的数对(△,□)应为 ▲ .
9.在算式30-△=4×□中的△、□分别填入一个正数,使它们的倒数和最小,则这两个数构成的数对(△,□)应为 ▲ .
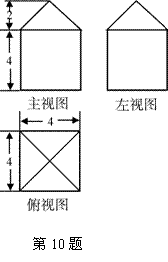
10.如果一个几何体的三视图如图所示(单位长度: cm),
则此几何体的表面积是 ▲ cm.
11.已知![]() 是等差数列
是等差数列![]() 的前n项和,且
的前n项和,且
![]() ,有下列四个命题:⑴
,有下列四个命题:⑴![]() ;⑵
;⑵![]() ;
;
⑶![]() ;⑷
;⑷![]() .其中正确命题的序号是 ▲.
.其中正确命题的序号是 ▲.
12.若函数![]() 的图象与x轴有公共点,则m的取值范围是 ▲.
的图象与x轴有公共点,则m的取值范围是 ▲.
13.在△ABC中,若![]() ,则
,则![]() = ▲
.
= ▲
.
14.设m,n是异面直线,则⑴一定存在平面![]() ,使
,使![]() ;⑵一定存在平面
;⑵一定存在平面![]() ,使
,使![]() ;⑶一定存在平面
;⑶一定存在平面![]() ,使m,n到
,使m,n到![]() 的距离相等;⑷一定存在无数对平面
的距离相等;⑷一定存在无数对平面![]() 和
和![]() ,使
,使![]() ;上述4个命题中正确命题的序号是 ▲.
;上述4个命题中正确命题的序号是 ▲.
二、解答题
15.(本题满分14分)
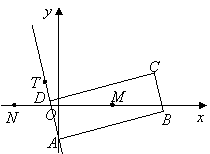 如图,矩形
如图,矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
,![]() 边所在直线的方程为
边所在直线的方程为![]() , 点
, 点![]() 在
在![]() 边所在直线上.
边所在直线上.
(1)求![]() 边所在直线的方程;
边所在直线的方程;
(2)求矩形![]() 外接圆的方程;
外接圆的方程;
16.(本题满分15分) 已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,设
,设![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求函数![]() 的最大值与最小值.
的最大值与最小值.
17.(本题满分15分) 建筑业中,建筑成本费用由城市土地使用权取得费和材料工程费二部分组成。某市今年的土地使用权取得费为2000元/![]() ;材料工程费在建造第一层时为400元/
;材料工程费在建造第一层时为400元/![]() ;以后每增加一层费用增加40元/
;以后每增加一层费用增加40元/![]() ;求楼高设计为多少层时,才能使平均每平方米建筑面积的成本费最省.
;求楼高设计为多少层时,才能使平均每平方米建筑面积的成本费最省.
18.(本题满分15分) 已知函数![]() .
.
(1)若![]() 的解集是
的解集是![]() ,求实数a,b的值;
,求实数a,b的值;
(2)若a为整数,b=a+2,且函数![]() 在
在![]() 上恰有一个零点,求a的值.
上恰有一个零点,求a的值.
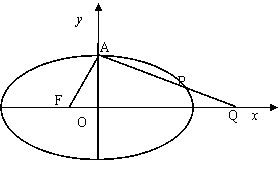
19.(本题满分15分) 设椭圆C:![]() 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且![]() .
.
 (1)求椭圆C的离心率;
(1)求椭圆C的离心率;
(2)若过A、Q、F三点的圆恰好与直线l:
![]() 相切,求椭圆C的方程.
相切,求椭圆C的方程.
20.(本题满分16分)幂函数y = 的图象上的点 Pn(tn2,tn)(n = 1,2,……)与 x 轴正半轴上的点 Qn 及原点 O 构成一系列正△PnQn-1Qn(Q0与O重合),记 an = QnQn-1
(1)求 a1的值;
(2)求数列 {an} 的通项公式 an;
(3)设 Sn为数列 {an} 的前 n 项和,若对于任意的实数 l∈[0,1],总存在自然数 k,当 n≥k时,3Sn-3n + 2≥(1-l) (3an-1) 恒成立,求 k 的最小值.

08届高三数学第五次调研考试
数学(文科)试卷答卷纸
 一、填空题(本大题共14小题,每小题5分,满分70分,把正确答案写在题中的横线上)
一、填空题(本大题共14小题,每小题5分,满分70分,把正确答案写在题中的横线上)
1.________________2. ________________3. ________________4. ________________
5. _______________ 6. ________________7. ________________8. ________________
9. _______________10. ________________
二、解答题
 15.(本题满分14分)
15.(本题满分14分)
16.(本题满分15分)

17.(本题满分15分)
 18.(本题满分15分)
18.(本题满分15分)
19.(本题满分15分)

 20.(本题满分16分)
20.(本题满分16分)
08届高三数学第五次调研考试
数学(文科)试卷参考答案
一、填空题(本大题共14小题,每小题5分,满分70分,把正确答案写在题中的横线上)
1.已知直线的斜率是-1,则它的倾斜角是 ![]() ▲
.
▲
.
2.已知集合![]() ,则
,则![]() 中元素的个数是▲ 0 .
中元素的个数是▲ 0 .
3.若复数![]() 是纯虚数,则实数 a的值是▲ -6 .
是纯虚数,则实数 a的值是▲ -6 .
4.已知向量![]() 若
若![]() ∥
∥![]() ,则x= ▲ 2 .
,则x= ▲ 2 .
5.抛物线的焦点是曲线![]() 的对称中心,顶点为坐标原点,则此抛物线的方程是 ▲
的对称中心,顶点为坐标原点,则此抛物线的方程是 ▲ ![]() .
.
6.利用简单随机抽样的方法,从n个个体(n>13)中逐个抽取13个个体,若第二次抽取时,余下的每个个体被抽取到的概率是![]() ,则在整个抽样过程中,每个个体被抽到的概率是
,则在整个抽样过程中,每个个体被抽到的概率是
▲ ![]() .
.
7.函数![]() 在区间
在区间![]() 上是减函数,则a的取值范围是
上是减函数,则a的取值范围是![]() ▲.
▲.
8.若椭圆![]() 的离心率是
的离心率是![]() ,则k的值是 ▲
,则k的值是 ▲ ![]() .
.
 9.在算式30-△=4×□中的△、□分别填入一个正数,使它们的倒数和最小,则这两个数构成的数对(△,□)应为 ▲ (10,5) .
9.在算式30-△=4×□中的△、□分别填入一个正数,使它们的倒数和最小,则这两个数构成的数对(△,□)应为 ▲ (10,5) .
10.如果一个几何体的三视图如图所示(单位长度: cm),
则此几何体的表面积是 ▲ ![]() cm
cm![]() .
.
11.已知![]() 是等差数列
是等差数列![]() 的前n项和,且
的前n项和,且
![]() ,有下列四个命题:⑴
,有下列四个命题:⑴![]() ;⑵
;⑵![]() ;
;
⑶![]() ;⑷
;⑷![]() .其中正确命题的序号是 ▲ ⑴⑵.
.其中正确命题的序号是 ▲ ⑴⑵.
12.若函数![]() 的图象与x轴有公共点,则m的取值范围是 ▲
的图象与x轴有公共点,则m的取值范围是 ▲![]() .
.
13.在△ABC中,若![]() ,则
,则![]() = ▲
= ▲ ![]() .
.
14.设m,n是异面直线,则⑴一定存在平面![]() ,使
,使![]() ;⑵一定存在平面
;⑵一定存在平面![]() ,使
,使![]() ;⑶一定存在平面
;⑶一定存在平面![]() ,使m,n到
,使m,n到![]() 的距离相等;⑷一定存在无数对平面
的距离相等;⑷一定存在无数对平面![]() 和
和![]() ,使
,使![]() ;上述4个命题中正确命题的序号是 ▲(1)(3)(4 ).
;上述4个命题中正确命题的序号是 ▲(1)(3)(4 ).
二、解答题
 15.(本题满分14分)
15.(本题满分14分)
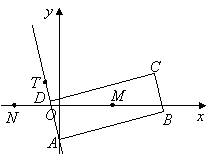
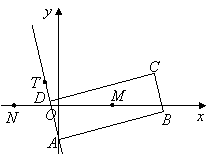
如图,矩形![]() 的两条对角线相交于点
的两条对角线相交于点![]() ,
,![]() 边所在直线的方程为
边所在直线的方程为![]() , 点
, 点![]() 在
在![]() 边所在直线上.
边所在直线上.
(I)求![]() 边所在直线的方程;
边所在直线的方程;
(II)求矩形![]() 外接圆的方程;
外接圆的方程;
15. 解:(I)因为![]() 边所在直线的方程为
边所在直线的方程为![]() ,且
,且![]() 与
与![]() 垂直,
垂直,
所以直线![]() 的斜率为
的斜率为![]() .
.
又因为点![]() 在直线
在直线![]() 上,
上,
所以![]() 边所在直线的方程为
边所在直线的方程为![]() .
.![]() .
.![]()
![]()
![]()
![]()
![]() 6分
6分
(II)由![]() 解得点
解得点![]() 的坐标为
的坐标为![]() ,
,
因为矩形![]() 两条对角线的交点为
两条对角线的交点为![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 10分
10分
所以![]() 为矩形
为矩形![]() 外接圆的圆心.
外接圆的圆心.
又![]() .
.
从而矩形![]() 外接圆的方程为
外接圆的方程为![]() .
.![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 14分
14分
16.(本题满分15分)
已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,设
,设![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)求函数![]() 的最大值与最小值.
的最大值与最小值.
16.解:(1)设![]() 中角
中角![]() 的对边分别为
的对边分别为![]() ,
,
则由![]() ,
,![]() ,
………………5分
,
………………5分
可得![]() ,所以
,所以![]() .
………………7分
.
………………7分
(2)![]()
![]()
![]() . ………………11分
. ………………11分
因为![]() ,
,![]() ,所以
,所以![]() . ………………14分
. ………………14分
即当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() . ………………15分
. ………………15分
17.(本题满分15分)
建筑业中,建筑成本费用由城市土地使用权取得费和材料工程费二部分组成。某市今年的土地使用权取得费为2000元/![]() ;材料工程费在建造第一层时为400元/
;材料工程费在建造第一层时为400元/![]() ;以后每增加一层费用增加40元/
;以后每增加一层费用增加40元/![]() ;求楼高设计为多少层时,才能使平均每平方米建筑面积的成本费最省.
;求楼高设计为多少层时,才能使平均每平方米建筑面积的成本费最省.
17.解:设楼高设计为n层时,平均每平方米建筑面积的成本费为y元.(n∈N+)![]() 2分
2分
依题意得:
y=![]()
=![]() =
=![]()
![]() =780
=780
(当且仅当n=10时,等号成立)
![]() 13分
13分
答:楼高设计为10层时,平均每平方米建筑面积的成本费最省. ![]() 15分
15分
18.(本题满分15分)
已知函数![]() .
.
(1)若![]() 的解集是
的解集是![]() ,求实数a,b的值;
,求实数a,b的值;
(2)若a为整数,b=a+2,且函数![]() 在
在![]() 上恰有一个零点,求a的值.
上恰有一个零点,求a的值.
18.解:(1)若不等式![]() 的解集是
的解集是![]() ,
,
则方程![]() 的两根是
的两根是![]() ,
……………… 4分
,
……………… 4分
所以![]() ,
,
所以![]() .
………………
7分
.
………………
7分
(2)因为b=a+2,
所以![]()
![]() 恒成立,
恒成立,
所以![]() 必有两个零点 ,
……………… 11分
必有两个零点 ,
……………… 11分
又因为函数![]() 在
在![]() 上恰有一个零点,
上恰有一个零点,
所以![]() 即
即![]() , ………………
13分
, ………………
13分
解得 ![]()
又![]() ……………… 15分
……………… 15分
19.(本题满分15分)
设椭圆C:![]() 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且![]() .
.
⑴求椭圆C的离心率;
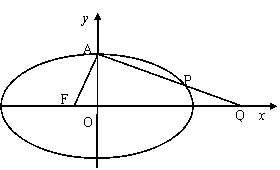 ⑵若过A、Q、F三点的圆恰好与直线l:
⑵若过A、Q、F三点的圆恰好与直线l:
![]() 相切,求椭圆C的方程.
相切,求椭圆C的方程.
解⑴设Q(x0,0),由F(-c,0)![]()
A(0,b)知![]()
![]()
设![]() ,
,
得![]() …2分
…2分
因为点P在椭圆上,所以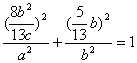 …………4分
…………4分
整理得2b2=3ac,即2(a2-c2)=3ac,![]() ,故椭圆的离心率e=
,故椭圆的离心率e=![]() ………6分
………6分
⑵由⑴知![]() ,………………………………7分
,………………………………7分
![]() ……………………………………………………9分
……………………………………………………9分
于是F(-![]() a,0) Q
a,0) Q![]() ,
,
△AQF的外接圆圆心为(![]() a,0),半径r=
a,0),半径r=![]() FQ=a……………………11分
FQ=a……………………11分
所以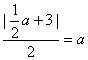 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b=![]() ,所求椭圆方程为
,所求椭圆方程为![]() ……15
……15
20、答案:(1) 由 P1(t12,t1)(t > 0),… 1分,得 kOP1 = = tan = Þ t1 =
∴ P1(,) …………2分
a1 = Q1Q0 = OP1 = …………5分
(2) 设 Pn(tn2,tn),得直线 PnQn-1的方程为:y-tn = (x-tn2)
可得 Qn-1(tn2-,0)
直线 PnQn的方程为:y-tn = -(x-tn2),可得 Qn(tn2 + ,0)
所以也有 Qn-1(tn-12 + ,0),得 tn2-= tn-12 + ,由 tn > 0,得 tn-tn-1 =
∴ tn = t1 + (n-1) = n …………8分
∴ Qn(n(n + 1),0),Qn-1(n(n-1),0)
∴ an = QnQn-1 = n …………10分
(3) 由已知对任意实数时 l∈[0,1] 时 n 2-2n + 2≥(1-l) (2n-1) 恒成立
Û 对任意实数 l∈[0,1] 时,(2n-1)l + n 2-4n + 3≥0 恒成立…………12分
则令 f (l) = (2n-1)l + n 2-4n + 3,则 f (l) 是关于 l 的一次函数.
Û 对任意实数 l∈[0,1] 时
Û …………14分
Û n≥3或n≤1
又 ∵ n∈N *
∴ k 的最小值为3…………16分