高三年级数学4月模拟考试
数学试题(理科)
命题人:吴校红
第Ⅰ卷(选择题,共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
|
|
A.A∪B B.A∩B C. D.
2.设![]() 均为第二象限角,且
均为第二象限角,且![]() ,则下列不等式成立的是 ( )
,则下列不等式成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.等差数列![]() 的公差d不为零,Sn是其前n项和,则下列四个命题中的假命题是( )
的公差d不为零,Sn是其前n项和,则下列四个命题中的假命题是( )
A.若d<0,且S3=S8,则{Sn}中,S5和S6都是{Sn}中的最大项
B.给定n,对于一定![]() ,都有
,都有![]()
C.若d>0,则{Sn}中一定有最小的项
D.存在![]() ,使
,使![]() 同号
同号
|
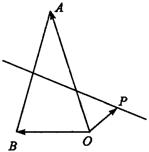
且P在线段AB的垂直平分线上,向量![]() 。若a=3,
。若a=3,
b=2,则c·(a-b)的值为 ( )
A.5 B.3
C.![]() D.
D.![]()
5.已知直线m⊥平面![]() ,直线n
,直线n![]() 平面
平面![]() ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )
A.若![]() B.若
B.若![]()
C.若![]() D.若
D.若![]()
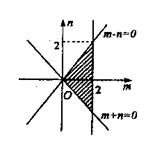
6.已知点M(a,b)在由不等式组 所在平面区域的面积是 ( )
所在平面区域的面积是 ( )
A.8 B.4 C.2 D.1
7.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
A.“至少有1个白球”与“都是白球”
B.“至少有1个白球”与“至少有1个红球”
C.“恰有1个白球”与“恰有2个白球”
D.“至少有1个白球”与“都是红球”
8.若![]() ,其中
,其中![]() ,且
,且![]() ,则实数(x,y)表示坐标平面上不同点的个数为 ( )
,则实数(x,y)表示坐标平面上不同点的个数为 ( )
A.50 B.70 C.90 D.120
9.已知直线![]() 某学生作了如下变形:由
某学生作了如下变形:由
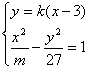 消去y后得到形如
消去y后得到形如![]() 的方程,当A=0时,该方程有一解;当A≠0时,
的方程,当A=0时,该方程有一解;当A≠0时,![]() 恒成立.假设学生的演算过程是正确的,则实数m的取值范围为 ( )
恒成立.假设学生的演算过程是正确的,则实数m的取值范围为 ( )
|
10.对于函数![]()
![]() ,令集合
,令集合![]() ,则集合M为 ( )
,则集合M为 ( )
A.空集 B.实数集 C.单元素集 D.二元素集
第Ⅱ卷(非选择题,共100分)
二、填空题(本大题共5小题,每小题5分,共25分。把答案填在答题卡的相应位置上。)
11.若![]() 的展开式中的第五项是
的展开式中的第五项是![]() ,则
,则![]() =
.
=
.
12.已知i是虚数单位,且函数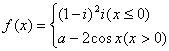 在R上连续,则实数a等于
在R上连续,则实数a等于
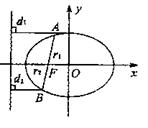
13.过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A,B两点,若![]() ,则椭圆的离心率e=
。
,则椭圆的离心率e=
。
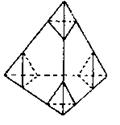
14.将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积为 。
15.已知函数![]() 时,
时,
![]() 只有一个实根;当k∈(0,4)时,
只有一个实根;当k∈(0,4)时,![]() 只有3个相异实根,现给出下列4个命题:
只有3个相异实根,现给出下列4个命题:
①![]() 有一个相同的实根;
有一个相同的实根;
②![]() ;有一个相同的实根;
;有一个相同的实根;
③![]() 的任一实根;
的任一实根;
④![]() 的任一实根.
的任一实根.
其中正确命题的序号是 。
三、解答题(本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤。)
|
已知函数![]()
(1)求函数![]() 的定义域;
的定义域;
(2)若![]() 是两个膜长为2的向量a,b的夹角,且不等式
是两个膜长为2的向量a,b的夹角,且不等式![]() 对于定义域内的任意实数x恒成立,求a+b的取值范围.
对于定义域内的任意实数x恒成立,求a+b的取值范围.
17.(本小题满分12分)
一个口袋中装有大小相同的2个白球和4个黑球。
(1)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(2)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
|
18.(本小题满分12分)
在平面直角坐标系中,已知三个点列{An},{Bn},{Cn},其中![]()
![]() ,满足向量
,满足向量![]() 与向量
与向量![]() 共线,且点(B,n)在方向向量为(1,6)的直线上
共线,且点(B,n)在方向向量为(1,6)的直线上![]()
(1)试用a与n表示![]() ;
;
(2)若a6与a7两项中至少有一项是an的最小值,试求a的取值范围。
19.(本小题满分12分)
|
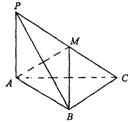
(1)求证:点P,A,B,C四点在同一球面上;
(2)求二面角A—MB—C的大小;
(3)求过P、A、B、C四点的球面中,A、B两点的球面距离。
20.(本小题满分13分)
|
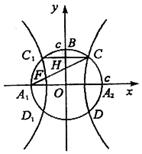
(1)当c=1时,求双曲线E的方程;
(2)试证:对任意正实数c,双曲线E的离心率为常数。
(3)连接A1C与双曲线E交于F,是否存在实数
![]() 恒成立,若存在,试求出
恒成立,若存在,试求出![]() 的值;
的值;
|
21.(本小题满分14分)
设函数![]() 处的切线的斜率分别为0,-a.
处的切线的斜率分别为0,-a.
(1)求证:![]() ;
;
(2)若函数f(x)的递增区间为[s,t],求s-t的取值范围.
(3)若当x≥k时,(k是a,b,c无关的常数),恒有![]() ,试求k的最小值.
,试求k的最小值.
高三年级数学4月模拟考试
数学试题(文科)参考答案
一、选择题
1.D 2.C 3.D 4.C 5.A 6.B 7.C 8.C 9.B 10.A
|
2.利用三角函数可知![]() 。故选C.
。故选C.
3.对于A ![]()
![]() 为最大,故A正确.
为最大,故A正确.
对于C,∵d>0,∴点(n,Sn)分布在开口向上的抛物线.故{Sn}中一定有最小的项,故C 正确.
4.设AB垂直平分线交AB于M,![]()
![]()
![]()
5.![]() 故选A.
故选A.
|
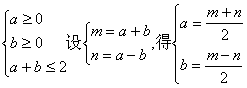
所以线性约束条件转化为: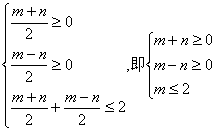
如图求得阴影部分的面积为:S=4
7.对于A,B,两事件不是互斥事件,对于D,两事件既是互斥的,也是对立的,故选C.
8.∵x,y均为三位数,且x+y=636,将和分为两类,一类是没有进位的,如123+513,一类是有进位的,如163+473;没有进位时,由于6=1+5=2+4=3+3,3=1+2
∴(x,y)共有5×2×5=50个;有进位时,个位不可能进位,只能十位进百位,故十位只能为7和6,从而百位只能为1和4与2和3,∴(x,y)共有4×2×5=40个,故总共有50+40=90个不同点.
9.由已知可推得直线与双曲线恒有公共点,
而直线过定点(3,0)
![]()
10.![]()
![]() 是以4为周期.
是以4为周期.
![]() ∴集合M为空集.
∴集合M为空集.
二、填空题
11.1 12.4 13.![]() 14.
14.![]() 15.①②④
15.①②④
提示:
11.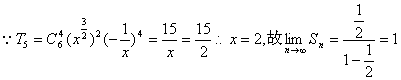
12.![]()
又![]()
|
![]() 注意到直线AB的倾斜角为60°
注意到直线AB的倾斜角为60°
![]()
|
表面减少三个小正三角形,增加一个正三角形,故表面积减少
![]() ,故所得几何体的表面积为
,故所得几何体的表面积为![]() .
.
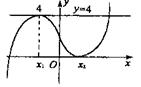
15.由k<0或k>4时,![]() 只有一个实数根可知,在k<0或k>4时,函数y=f(x)与y=k的图象只有一个交点;0<k<4时,函数y=f(x)与y=k的图象有三个交 点;故函数的极值点有两个,极值分别为0和4,
只有一个实数根可知,在k<0或k>4时,函数y=f(x)与y=k的图象只有一个交点;0<k<4时,函数y=f(x)与y=k的图象有三个交 点;故函数的极值点有两个,极值分别为0和4,
|
有两根x1,x2,
且![]()
所以x1是 ![]() 的根,x2是
的根,x2是![]() 的根,所以①,②对;将y=f(x)的图象向下平移1个单位得y=f(x)-1的图象,向上平移3个单位得y=f(x)+3的图象,由图象知③错;将y=f(x)的图象向上平移5个单位得y=f(x)+5的图象,将y=f(x)的图象向下平移2个单位得y=f(x)-2的图象,由图象知④对.
的根,所以①,②对;将y=f(x)的图象向下平移1个单位得y=f(x)-1的图象,向上平移3个单位得y=f(x)+3的图象,由图象知③错;将y=f(x)的图象向上平移5个单位得y=f(x)+5的图象,将y=f(x)的图象向下平移2个单位得y=f(x)-2的图象,由图象知④对.
三、解答题
16.(1)若原函数有意义,则![]()
故![]()
(2)因为![]()
故函数f(x)的最大值为![]() 恒成立,只需
恒成立,只需![]()
故![]()
故![]()
17.解法一 “有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,记“有放回摸球两次,两球恰好颜色不同”为事件A,
∵“两球恰好颜色不同”共2×4+4×2=16种可能,![]()
解法二 “有放回摸取”可看作独立重复实验
∵每次摸出一球得白球的概率为![]()
∴“有放回摸两次,颜色不同”的概率为![]()
(2)设摸得白球的个数为![]() ,依题意得
,依题意得
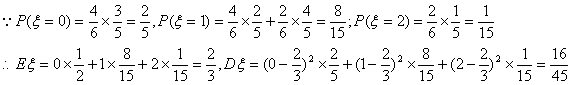 18.(1)
18.(1)![]()
又∵{Bn}在方向向量为(1,6)的直线上,![]()
![]()
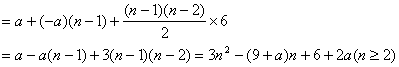
(2)∵二次函数![]() 是开口向上,对称轴为
是开口向上,对称轴为![]() 的抛物线
的抛物线
又因为在a6与a7两项中至少有一项是数列{an}的最小项,
∴对称轴![]()
19.(1)证明:由已知条件Rt△PAC中PM=MC,则MP=MC=MA

则MC=MB=MP,所以MP=MC=MA=MB,即P,A,B,C四点都在以M为球心,半径为PM的球面上,
(2)以AC为y轴,AP为z轴建立如图所示的空间直角坐标系A—xyz,
则B(![]()
设平面AMB的法向量为![]()
由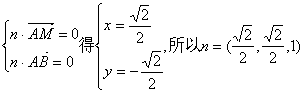
同理设平面BMC的法向量为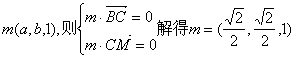
所以![]() 故二面角A—MB—C的大小为120°.
故二面角A—MB—C的大小为120°.
(3)∵过P,A,B,C四点的球面的球心为M,半径为![]()
在![]()
故A、B两点的球面距离为![]() .
.
20.(1)由c=1知B(0,1),∵![]() , ∴
, ∴![]()
即
![]() 点C在单位圆上,∴
点C在单位圆上,∴![]()
设双曲线E的方程为 ![]()
由点C的双曲线E上,半焦距c=1有: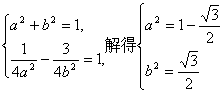
所以双曲线E的方程为: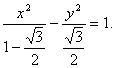
(2)证明:∵A1(-c,0),B(0,c),由 ![]()
设双曲线E的方程为 ![]() ∴
∴ 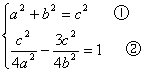
①代入②,化简整理得
![]()
解得
![]()
又
![]()
∴![]() ,即双曲线E的离心离是与c无关的常数。
,即双曲线E的离心离是与c无关的常数。
(3)假设存在实数![]()
有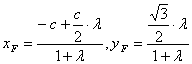
点F![]() 点C,F都在双曲线E上,故有
点C,F都在双曲线E上,故有
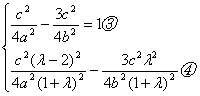
由③得![]() ⑤
⑤
⑤代入④得![]()
即![]()
故存在实数![]() 恒成立.
恒成立.
21.(1)![]() 由题意及导数的几何意义得
由题意及导数的几何意义得
![]() ①
①
![]() ②
②
又![]()
由①得![]() ③
③
将c=-a-2b代入②得![]() 有实根,
有实根,
故判别式![]() ④
④
由③、④得![]()
(2)由![]()
知方程![]() 有两个不等实根,设为x1,x2,
有两个不等实根,设为x1,x2,
又由![]() (*)的一个实根,
(*)的一个实根,
则由根与系数的关系得![]()
当x<x2,或x>x1时,![]()
故函数f(x)的递增区间为[x2,x1],由题设知[x2,x1]=[s,t],
因此![]()
(3)由![]()
![]()
因此a<0,得![]()
设![]() 的一次函数,由题意,
的一次函数,由题意,
![]() 恒成立故
恒成立故![]()
由题意![]()