高三年级数学4月模拟考试2

高三年级数学4月模拟考试

数学试题（文科）

命题人：吴校红

第Ⅰ卷（选择题，共50分）

一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.）

1．已知全集U={1，2，3，4，5，6，7，8}，A={3，4，5}，B={1，3，6}，则集合C={2，7，8}是　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．A∪B　　　　　　　　　B．A∩B　　　　　　　　　C．　　　　　　　　　　　　　D．

2．设均为第二象限角，且，则下列不等式成立的是　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　 D．

3．等差数列的公差d不为零，S_n是其前n项和，则下列四个命题中的假命题是（　　）

　　　 A．若d<0，且S₃=S₈，则{S_n}中，S₅和S₆都是{S_n}中的最大项

　　　 B．给定n，对于一定，都有

　　　 C．若d>0，则{S_n}中一定有最小的项

　　　 D．存在，使同号

4．如图，P为△AOB所在平面上一点，向量，

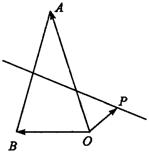
且P在线段AB的垂直平分线上，向量。若a=3，

b=2，则c·（a－b）的值为　　　　　　　  （　　）

　　　 A．5　　　　　　　　　　　　B．3　　　　　　　　　　　　

　　　 C．　　　　　　　　　　　D．

5．已知直线m⊥平面，直线n平面，则下列命题正确的是　　　　　　　　　　　　　（　　）

　　　 A．若　　　　　　　　　　　　　 B．若

　　　 C．若　　　　　　　　　　　　　D．若

6．在坐标平面上，不等式组所表示的平面区域的面积为　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　 D．2

7．从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是（　　）

　　　 A．“至少有1个白球”与“都是白球”

　　　 B．“至少有1个白球”与“至少有1个红球”

　　　 C．“恰有1个白球”与“恰有2个白球”

　　　 D．“至少有1个白球”与“都是红球”

8．若，其中，且，则实数（x，y）表示坐标平面上不同点的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．50　　　　　　　　　　　B．70　　　　　　　　　　　 C．90　　　　　　　　　　　D．120

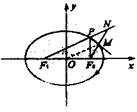
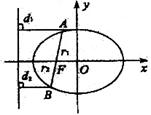
9．P是以F₁、F₂为焦点的椭圆上的一点，过焦点F₂作∠F₁PF₂外角平分线的垂线，垂足为M，则点M的轨迹是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．圆　　　　　　　　　　　B．椭圆　　　　　　　　　 C．双曲线　　　　　　　 D．抛物线

10．对于函数

1,3,5

，令集合，则集合M为　　　　 （　　）

　　　 A．空集　　　　　　　　　 B．实数集　　　　　　　　C．单元素集　　　　　　D．二元素集

第Ⅱ卷（非选择题，共100分）

二、填空题（本大题共5小题，每小题5分，共25分。把答案填在答题卡的相应位置上。）

11．若展开式中只有第四项系数最大，那么它的常数项为　　　　 。

12．已知100个数据a₁，a₂，a₃，……，a₁₀₀的平均数是88，数据a₁，a₂，a₃，……，a₄₀的平均数为80，数据a₄₁，a₄₂，a₄₃，……，a₈₀的平均数为90，则数据a₈₁，a₈₂，a₈₃，……，a₁₀₀的平均数为　　　　　　　　 。

13．过椭圆的左焦点F且倾斜角为60°的直线交椭圆于A，B两点，若，则椭圆的离心率e=　　　　　　　  。

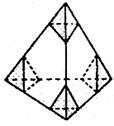
14．将棱长为3的正四面体以各顶点截去四个棱长为1的小正四面体（使截面平行于底面），所得几何体的表面积为　　　　　　　　 。

15．如果函数的导函数的图象如下图所示，给出下列命题：

　　①函数在区间内单调递减；

②函数在区间（4，5）内单调递增；

③当时，函数有极小值；

④当时，函数有极大值。

其中正确命题的序号是　　　　　　　  。

三、解答题（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤。）

16．（本小题满分12分）

　　已知函数

　 （1）求函数的定义域；

1,3,5

　 （2）若是两个膜长为2的向量a，b的夹角，且不等式对于定义内的任意实数x恒成立，求a+b的取值范围.

17．（本小题满分12分）

　　一个口袋中装有大小相同的2个白球和4个黑球。

　 （1）采取放回抽样方式，从中摸出两个球，求两球恰好颜色不同的概率；

　 （2）采取不放回抽样方式，从中摸出两个球，求两球恰好颜色不同的概率。

18．（本小题满分12分）

　　　　在平面直角坐标系中，已知三个点列{A_n}，{B_n}，{C_n}，其中

　　，满足向量与向量共线，且

　 （1）试用a与n表示；

　 （2）若a₆与a₇两项中至少有一项是a_n的最小值，试求a的取值范围。

19．（本小题满分12分）

　　　　在三棱锥P—ABC中，PA⊥底面ABC，PA=AB=BC=2，∠ABC=90°，M为棱PC的中点。

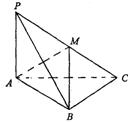
　 （1）求证：点P，A，B，C四点在同一球面上；

　 （2）求二面角A—MB—C的大小；

　 （3）求过P、A、B、C四点的球面中，A、B两点的球面距离。

	1,3,5

20．（本小题满分13分）

如图，以A₁，A₂为焦点的双曲线E与半径为c的圆O相交于C，D，C₁，D₁，连接CC₁与OB交于点H，且有：。其中A₁，A₂，B是圆O与坐标轴的交点，c为双曲线的半焦距。

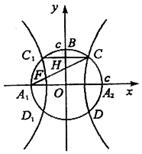
　 （1）当c=1时，求双曲线E的方程；

 （2）试证：对任意正实数c，双曲线E的离心率为常数。

21．（本小题满分14分）

设函数

　 （1）若且对任意实数均有成立，求表达式；

　 （2）在（1）在条件下，当是单调函数，求实数k的取值范围；

　 （3）设mn<0，m+n>0，a>0且为偶函数，证明

高三年级数学4月模拟考试

数学试题（文科）参考答案

一、选择题

1.D  2.C　3.D　4.C  5.A　6.B　7.C  8.C　9.A　10.A

1,3,5

提示：

2．利用三角函数可知。故选C.

3．对于A　

　 为最大，故A正确.

　 对于C，∵d＞0，∴点（n，S_n）分布在开口向上的抛物线.故{S_n}中一定有最小的项，故C 正确. 对于D ，故选D。

4．设AB垂直平分线交AB于M，

　

　

5．故选A.

6．作出不等式组表示的平面区域如图，阴影部分面积为

7．对于A，B，两事件不是互斥事件，对于D，两事件既是互斥的，也是对立的，故选C.

8．∴x，y均为三位数，且x+y=636，将和分为两类，一类是没有进位的，如123+513，一类是有进位的，如163+473；没有进位时，由于6=1+5=2+4=3+3，3=1+2

∴（x，y）共有5×2×5=50个；有进位时，个位不可能进位，只能十位进百位，故十位只能为7和6，从而百位只能为1和4与2和3，∴（x，y）共有4×2×5=40个，故总共有50+40=90个不同点.

9．延长F₂M交F₁P延长线于N，则F₂M=MN，PF₂=PN，

　 又∵O为F₁F₂的中点。

　 ∴

  （定值）故M点轨迹是圆。

10．

　  是以4为周期.

　 ∴集合M为空集.

二、填空题

11．15　　12．100　 13．　 14．　　15．②③

提示：

11．∵展开式中只有第四项系数最大。　∴n=6。

故，∴常数项为T₃=15

12．设所求平均数为x。则

13．如图，由椭圆的第二定义得　，两式相减得

。注意到直线AB的倾斜解为60°。

∴

∴

14．原正四面体的表面积为 ，每截去一个

小正四面体，表面减少三个小正三角形，增加一个小正

三角形，故表面积减少，故所得几何

体的表面积为

15．当递增。　∴①错；

当递增，故②对；

∴处左“－”，右“+”，

∴在得取极小值，故③对；由 处左，右均为正值知在处无极值，　∴④错。

三、解答题

16．（1）若原函数有意义，则

故

（2）因为

故函数f（x）的最大值为恒成立，只需

故

故

17．解法一 “有放回摸两次，颜色不同”指“先白再黑”或“先黑再白”，记“有放回摸球两次，两球恰好颜色不同”为事件A，

∵“两球恰好颜色不同”共2×4+4×2=16种可能，

解法二　“有放回摸取”可看作独立重复实验

∵每次摸出一球得白球的概率为

∴“有放回摸两次，颜色不同”的概率为

（2）记“摸出两个球，两球恰好颜色不同”为B，摸出两个球共有方法种，

其中两球一白一黑有

18．（1）

又∵{B_n}在方向向量为（1，6）的直线上，

　

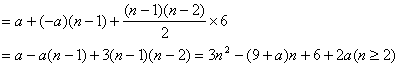
（2）∵二次函数是开口向上，对称轴为的抛物线

又因为在a₆与a₇两项中至少有一项是数列{a_n}的最小项，

∴对称轴

19．（1）证明：由已知条件Rt△PAC中PM=MC，则MP=MC=MA

则MC=MB=MP，所以MP=MC=MA=MB，即P，A，B，C四点都在以M为球心，半径为PM的球面上，

（2）以AC为y轴，AP为z轴建立如图所示的空间直角坐标系A—xyz，

则B（

设平面AMB的法向量为

由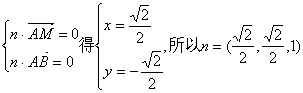

同理设平面BMC的法向量为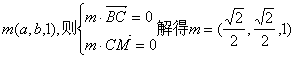

所以故二面角A—MB—C的大小为120°.

（3）∵过P，A，B，C四点的球面的球心为，半径为

在

故A、B两点的球面距离为.

20．（1）由c=1知B（0，1），∵， ∴

即  点C在单位圆上，∴

设双曲线E的方程为　

由点C的双曲线E上，半焦距c=1有：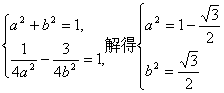

所以双曲线E的方程为：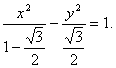

（2）证明：∵A₁（－c，0），B（0，c），由

设双曲线E的方程为  ∴  

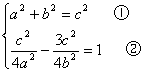
①代入②，化简整理得

解得

又

∴，即双曲线E的离心离是与c无关的常数。

21．（1）∵，∴恒成立知：

，

∴a=1，从而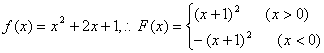

（2）由（1）知

由在[－2，2]上是单调函数知：

（3）∵是偶函数，∴为增函数，对于，

当

，∴是奇函数，且是在上为增函数，

当mn<0，m、n异号，

 ∴

，

∴

综上可知