高三年级数学上学期期末考试
数学(理)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合![]() 则(
则(![]()
![]() )
)![]() (
(![]()
![]() )=( )
)=( )
A.![]()
![]() B.{4} C.{1,3,5} D.{1,2,3,5}
B.{4} C.{1,3,5} D.{1,2,3,5}
2.定义![]() ,则
,则![]() ( )
( )
A.![]() B.0 C.
B.0 C.![]() D.
D.![]()
3.给出下列三个命题:
①正四棱柱一定是直平行六面体;
②四面体![]() 中,若点
中,若点![]() 在面
在面![]() 上的射影是
上的射影是![]() 的垂心,则点
的垂心,则点![]() 在面
在面![]() 上的射影也是
上的射影也是![]() 的垂心;
的垂心;
③经过球面上不同两点的球的小圆可能不存在.
其中假命题的个数为 ( )
A.0个 B.1个 C.2个 D.3个
4.![]() ( )
( )
A.1 B.-1 C.1或-1 D.无法确定
5.![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.某天下午的课程表要排入物理、化学、生物和两节自习共5节课,如果第1节不
排生物,最后1节不排物理,那么不同的排课表的方法有 ( )
A.36种 B.39 种 C.60种 D.78种
7.已知实系数一元二次方程![]() 的两个实根为
的两个实根为![]() 、
、![]() ,并且
,并且
![]() ,则
,则![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.过抛物线![]() 准线上任一点作抛物线的切线,切点分别为A、B,则直线AB恒过点
准线上任一点作抛物线的切线,切点分别为A、B,则直线AB恒过点
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
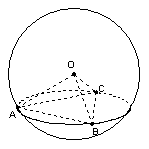 9.如图,
9.如图,![]() 是表面积为
是表面积为![]() 的球面上的点,且
的球面上的点,且![]() ,
,![]() ,
,![]() ,
,![]() 为球心,则直线
为球心,则直线![]() 与截面
与截面![]() 所成角的大小是 ( )
所成角的大小是 ( )
| |
C.arccos![]() D.arccos
D.arccos![]()
10.已知函数![]() ,
,![]() 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当![]() 时,
时,![]() =
=![]()
则方程![]() 不相等的实数根的个数是
( )
不相等的实数根的个数是
( )
A.3 B.2 C.1 D.0
11.已知![]() ,且函数
,且函数![]() 在
在![]() ,
,![]() 上存在反函数,则 ( )
上存在反函数,则 ( )
A.![]() B.
B.![]()
C.![]() ∪
∪![]() D.
D.![]()
12.已知周期数列![]() 满足
满足![]() ,若
,若![]() ,则当该数列的周期最小时,数列的前2008项的和是
( )
,则当该数列的周期最小时,数列的前2008项的和是
( )
A.1338 B.1339 C.1340 D.1341
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题纸上.
13.在![]() 的展开式中,含
的展开式中,含![]() 项的系数为_________.
项的系数为_________.
14.若将形如![]() 的函数称为线性分式函数,则图象关于直线
的函数称为线性分式函数,则图象关于直线![]() 对称的一个线性分式函数的解析式可以为_________.(写出你认为正确的一个解析式即可)
对称的一个线性分式函数的解析式可以为_________.(写出你认为正确的一个解析式即可)
15.若随机从集合![]() 中选出两个不同的元素
中选出两个不同的元素![]() ,则
,则![]() 为整数的概率为_________.
为整数的概率为_________.
16.已知点![]() 是双曲线
是双曲线![]() 上一动点,
上一动点,![]() 是双曲线的两个焦点,
是双曲线的两个焦点,![]() 是坐标原点,则
是坐标原点,则![]() 取值范围是_________ .
取值范围是_________ .
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
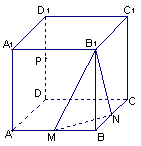 如图,棱长为1的正方体
如图,棱长为1的正方体![]() 中,点
中,点![]() 分别为棱
分别为棱![]() 、
、
![]() 、
、![]() 的中点.
的中点.
(1)求二面角![]() 的正切值;
的正切值;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
| |
18.(本小题满分12分)
设函数![]() ,
,![]()
(1)求函数![]() 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)当![]() 时,函数
时,函数![]() 的最小值为1,求此时
的最小值为1,求此时![]() 的最大值及相应
的最大值及相应![]() 值.
值.
19.(本小题满分12分)
某轮船公司争取到一个相距![]() 海里的甲、乙两地的客运航线权,已知轮船的平均载客人数为
海里的甲、乙两地的客运航线权,已知轮船的平均载客人数为![]() 人,轮船每小时使用的燃料费和轮船航行速度的关系为
人,轮船每小时使用的燃料费和轮船航行速度的关系为![]()
![]() ,轮船的最大速度为
,轮船的最大速度为![]() 海里/小时,其余费用(不论速度如何)总计是每小时
海里/小时,其余费用(不论速度如何)总计是每小时![]() 元.假定轮船从甲地到乙地匀速航行,若公司打算从每位乘客身上获得利润
元.假定轮船从甲地到乙地匀速航行,若公司打算从每位乘客身上获得利润![]() 元,试为该轮船公司设计一个较为合理的船票价格.
元,试为该轮船公司设计一个较为合理的船票价格.
20.(本小题满分12分)
已知椭圆的方程为 ![]() , 过其左焦点
, 过其左焦点![]() 斜率为1的直线交椭圆于
斜率为1的直线交椭圆于![]() 两点.
两点.
(1)若![]() 与
与![]() 共线,求椭圆的方程;
共线,求椭圆的方程;
(2)若在左准线上存在点![]() , 使
, 使![]() 为正三角形, 求椭圆的离心率
为正三角形, 求椭圆的离心率![]() .
.
21.(本小题满分12分)

(1)![]()
(2)![]()
22.(本小题满分14分)
已知函数![]() ,
,![]() ,
,![]()
(1)证明:当![]() 时,恒有
时,恒有![]()
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;
(3)在![]() 轴正半轴上有一动点
轴正半轴上有一动点![]() ,过
,过![]() 作
作![]() 轴的垂线依次交函数
轴的垂线依次交函数![]() 的图象于点
的图象于点![]() ,
,![]() 为坐标原点.试将
为坐标原点.试将![]() 与
与![]() 的面积比表示为
的面积比表示为![]() 的函数
的函数![]() ,并判断
,并判断![]() 是否存在极值,若存在,求出极值;若不存在,说明理由.
是否存在极值,若存在,求出极值;若不存在,说明理由.
参 考 答 案
一、选择题
1.D;2.C;3.A;4.B;5.D ; 6.B;
7.C;8.A;9.D;10.B ; 11.C; 12.B.
二、填空题:
13.164 14.![]() (答案不唯一) 15.
(答案不唯一) 15.![]() 16.
16.![]()
三、解答题:
17.(1)解:连结![]() ,交
,交![]() 于
于![]() ,连结
,连结![]()
![]()
![]() //
//![]()
![]()

![]()
![]()
(2)连结![]() .
.
由(1)知![]()
![]()
![]()
![]()
![]() ……6分
……6分
![]()
![]()

18.解:![]() =
=
![]() =
=![]() ……4分
……4分
(1)![]() 的最小正周期
的最小正周期![]() ,
,
由![]() 得
得![]() ,
,
故![]() 的单调递增区间为
的单调递增区间为![]() ……8分
……8分
(2)![]() ,当
,当![]() 时,原函数最小值为1,即
时,原函数最小值为1,即![]() ,
,![]() ,当
,当![]() 时,
时,![]() 的最大值为
的最大值为![]() .……12分
.……12分
19.解:设从甲地到乙地的人均总费用为![]() ,则
,则![]() ,
,
即 ![]() , ……3分
, ……3分
![]() 由
由![]() 得
得![]()
当![]() 时,
时,![]() 此时
此时
![]() 单调递减,
单调递减,
因此当![]() ,
,![]() 最小为(
最小为(![]() +
+![]() )元.
)元.
所以较为合理的船票价格为(![]() +
+![]() )元.……7分
)元.……7分
当![]() 时,
时,![]() 此时
此时
![]()
因此当![]() =
=![]() 时,
时,![]() 最小为
最小为![]() 元.
元.
所以较为合理的船票价格为(![]() +10)元.……11分
+10)元.……11分
综上,当![]() 时,较为合理的船票价格为(
时,较为合理的船票价格为(![]() +
+![]() )元;
)元;
当![]() 时,较为合理的船票价格为(
时,较为合理的船票价格为(![]() +10)元.……12分
+10)元.……12分
20.解:(1)将直线PQ的方程为![]()
化简得![]() .
.
令![]() 则
则 ![]()
由![]() ,
,![]() 与
与![]() 共线,得
共线,得
![]()
∴![]()
∴![]() ,即
,即![]() ,∴
,∴![]() ……4分
……4分
又![]()
 所以椭圆的方程为
所以椭圆的方程为![]() .
……6分
.
……6分
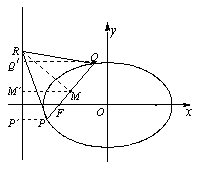
(2)如图, 设线段
![]() 的中点为
的中点为 ![]() .
.
过点 ![]() 、
、![]() 、
、![]() 分别作准线的垂线,
分别作准线的垂线,
垂足分别为 ![]() 、
、![]() 、
、![]() , 则
, 则
![]() .
.
![]()
又![]() ,
,![]()
![]() ,所以
,所以![]() .
.
……12分
21.解:
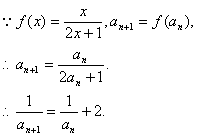


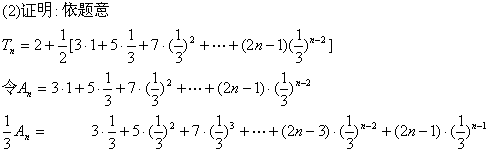
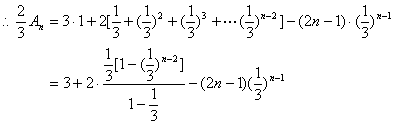
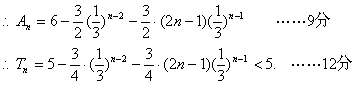
22.解:(1)设![]() ,则
,则![]() =
=![]() ,……2分
,……2分
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在(0,
在(0,![]() 单调递增,又
单调递增,又![]()
在![]() 处连续,所以
处连续,所以![]() ,即
,即![]() ,
,
所以![]() 。……4分
。……4分
(2)设![]() ,
,
则![]() 在(0,
在(0,![]() 恒大于0,
恒大于0,![]() ,
,
![]() ,……6分
,……6分
![]() 的根为0和
的根为0和![]()
即在区间(0,![]() 上,
上,![]() 的根为0和
的根为0和![]()
若![]() ,则
,则![]() 在
在![]() 单调递减,
单调递减,
且![]() ,与
,与![]() 在(0,
在(0,![]() 恒大于0矛盾;
恒大于0矛盾;
若![]() ,
,![]() 在(0,
在(0,![]() 单调递增,
单调递增,
且![]() ,满足题设条件,所以
,满足题设条件,所以![]() ,所以
,所以![]() ……9分
……9分
(3)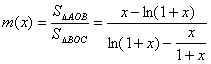
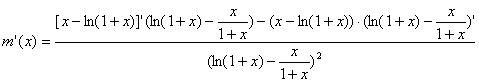
其分母为正数,其分子为:
![]()
![]() ……12分
……12分
由第(2)问知:![]() 在
在![]() 恒成立,
恒成立,
所以![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 为单调递增函数,
为单调递增函数,
故![]() 而无极值.……14分
而无极值.……14分