高三年级数学十一月月考试题
数 学 试 题（文）
命题：霍祝华 审稿：王宪生 校对：张科元
第Ⅰ卷（选择题，共50分）
一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．集合P={1，4，9，16，…}，若
，则
，则运算
可能是（ ）
A．加法 B．减法 C．乘法 D．除法
2．若
，则
值为（ ）
A．
B．
C．
D．
3．已知不等式
的解集是
，则实数a的值是（ ）
A．－3 B．3 C．－1 D．1
4．已知函数
在区间
上的最大值和最小值之和为a，则a的值为（ ）
A．
B．
C．2 D．4
5．等差数列{an}中，a1>0，公差d<0, Sn为其前n项和，对任意自然数n，若点（n, Sn）在以下4条曲线中的某一条上，则这条曲线应是（ ）
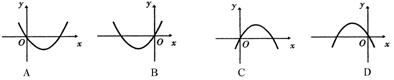
6．一小商贩准备用50元钱在一批发市场购买甲、乙两种小商品，甲每件4元，乙每件7元。甲商品每件卖出去后可赚1元钱，乙每件卖出去后可赚1.8元钱. 若要使赚的钱最多，那么该商贩购买甲、乙两种商品的件数应分别为（ ）
A．甲7件，乙3件 B．甲9件，乙2件
C．甲4件，乙5件 D．甲2件，乙6件
7．若
（ ）
A．（2，1） B．（－2，1） C．（1，－2） D．（－2，－1）
8．若某等差数列{an}中，
为一个确定的常数，则下列各个和中也为确定的常数的是（ ）
A．S17 B．S10 C．S8 D．S15
9．下列命题正确的有（ ）
（1）存在角
，使得
（2）若
为第一象限角，且
，则
；
（3）直线
是函数
图象的一条对称轴；
（4）将
的图象向左平移
个单位即可得到
的图象
A．0个 B．1个 C．2个 D．3个
10．设实数x1，x2满足
，则
的大小关系为（ ）
A．
B．
C．
D．不能确定，它们的大小与a有关
第Ⅱ卷（非选择题，共100分）
二、填空题：本大题共5小题，每小题5分，共25分. 把答案填在答题卡的相应位置上.
11．已知向量a与b的夹角为60°，
且
，则a等于____.
12．定义在R上的函数f(x)的周期为
，若在区间
上，
，那么在区间[
]上
的解析式是
____________.
13．不等式
表示的平面区域内必包含（0，0）及（1，1）两点，则k的取值范围为_____________.
14．设数列{an}的前n项和Sn，令
，称Tn为数列a1，a2，…，an的“理想数”. 已知数列a1, a2, …，a500的“理想数”为2004，那么数列7，a1, a2,…，a500的“理想数”为_________.
15．设函数f(x)的定义域为D，如果对于任意的
，存在唯一的
，使
（C为常数）成立，则称函数在D上均值为C. 下列5个函数：①
； ②
； ③
； ④
； ⑤
则满足在其定义域上均值为2的所有函数的序号是_______________.
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 11 | 12 | 13 | 14 | 15 | |||||
| 答案 | ||||||||||
三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.
16．（本小题满分12分）
设在平面上有两个向量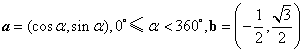
.
（1）试证：两向量a+b与a－b垂直；
（2）两个向量
的模相等时，求角
17．（本小题满分12分）
某公司准备进行两种组合投资，稳健型组合投资是由每份金融投资20万元，房地产投资30万元组成；进取型组合投资是由每份金融投资40万元，房地产投资30万元组成. 已知每份稳健型组合投资每年可获利10万元，每份进取型投资每年可获利15万元. 若可作投资用的资金名，金融投资不超过160万元，房地产投资不超过180万元，那么这两种组合投资应注入多少份，能使一年获利总额最多？
18．（本小题满分12分）
已知函数
，其中
（1）判断函数的单调性；
（2）若命题p：
为真命题，求实数x的取值范围.
19．（本小题满分12分）
已知函数
的图象经过点A（0，1），
，且当
时，取最大值
（1）求的解析式；
（2）是否存在向量m，使得将的图象按向量m平移后可以得到一个奇函数的图象，若能，求出满足条件的一个m；若不能，请说明理由.
20．（本小题满分13分）
设各项均为正数的数列{an}满足：
.
（1）求首项a1和数列{an}的通项公式；
（2）设数列{an}的前n项和为Sn，且
，求实数
的值.
21．（本小题满分14分）
已知函数
具有下列性质：
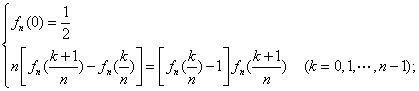
（1）当n一定，记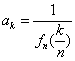
，求
的表达式 （k=0, 1, …，n）；
（2）对
，证明
.