南县一中高三文科数学调研考试试卷
命题人:王正飞 2007.4.20
一、选择题:(本大题共10小题,每小题5分,共50分)
1. 已知集合M=![]() ,集合N=
,集合N=![]() ,那么当y=0时有( )
,那么当y=0时有( )
A.M=N={2,-2} B.M ={2,-2},N={(2,0),(-2 ,0)}
C.M=N={(2,-2)} D. M ={2,-2},N={(2,-2)}
2. 函数![]() 的值域为( )
的值域为( )
A ![]() B
B![]() C (-1,1)
D
C (-1,1)
D ![]()
3.已知角![]() 的终边过P(-6a,-8a)(
的终边过P(-6a,-8a)(![]() ),则
),则![]() 的值为( )
的值为( )
A.![]() B.
B. ![]() C.
C.![]() 或
或![]() D.
D. ![]() 或
或![]()

5.直线y+mx+m+1=0与圆x2+y2=2的位置关系为( )
A.相离 B.相切 C.相交 D. 相交或相切
6. 以下命题中正确的是( )
A. ![]() 恒成立;
恒成立;
B. △ABC中,若![]() ,则△ABC是等腰三角形;
,则△ABC是等腰三角形;
C.对等差数列{an}前n项和Sn,若对任意正整数n都有Sn+1>Sn,则an+1>an对任意正整数n恒成立;
D.a=3是直线ax+2y+3a=0与直线3x+(a-1)y=a-7平行且不重合的充要条件;
7.已知![]() 的展开式中,
的展开式中,![]() 的系数为56,则实数a的值为( )
的系数为56,则实数a的值为( )
A.5或6 B.-1或4 C.6或-1 D.4或5
8.已知双曲线中心在原点且一个焦点为F(![]() ,直线y=x-1与其相交于M、N两点,MN中点的横坐标为
,直线y=x-1与其相交于M、N两点,MN中点的横坐标为![]() ,则此双曲线的方程是( )
,则此双曲线的方程是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
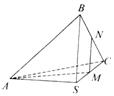 9.如图所示,在正三棱锥
9.如图所示,在正三棱锥![]() 中,M、N分别是SC、BC的中点,且
中,M、N分别是SC、BC的中点,且![]() ,若侧棱
,若侧棱![]() ,则正三棱锥
,则正三棱锥![]() 外接球的表面积是
外接球的表面积是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
10. 设函数f(x)的定义域为R,若存在与x无关的正常数M,使![]() 对一切实数x均成立,则称f(x)为“有界泛函”,给出以下函数:①f(x) =x2,②f(x)=2x,③
对一切实数x均成立,则称f(x)为“有界泛函”,给出以下函数:①f(x) =x2,②f(x)=2x,③![]()
④![]() 其中是“有界泛函”的个数为 ( )
其中是“有界泛函”的个数为 ( )
A.0 B.1 C.2 D.3
二.填空题(共5小题,每小题5分,共25分)
11. 某校共有2400名学生,其中男生1300名,女生1100名,用分层抽样法抽取一个容量为120的样本,则女生被抽取的人数为_________;
12. 平面直角坐标系中有五个点,分别为O(0,0)、A(1,2)、B(2,4)、C(-1,2)、D(-4,4),则这五个点一共可确定不同(顶点不全相同)的三角形个数为
13.等比数列![]() 是递增数列,其前n项的积为Tn,若T13 =4T9,则a8•a15=
________;
是递增数列,其前n项的积为Tn,若T13 =4T9,则a8•a15=
________;
14. 曲线![]() 上的点P到A(1,1)的最小距离为________ ;
上的点P到A(1,1)的最小距离为________ ;
15加工火腿肠的主要原料是精肉和面粉.若A、B两种火腿肠的精肉和面粉的搭配如下表,且A、B的价格分别为0.6元/支、0.8元/支.现有精肉2吨,面粉2.5吨,用以加工A、B两种火腿肠。假设产品供不应求,那么可以获得的最大销售额为 .
| 原料 产品 | 精肉(千克) | 面粉(千克) |
| A(千支) | 20 | 30 |
| B(千支) | 30 | 20 |
三.解答题:(共75分)
16.(本小题满分12分)
已知向量![]()
![]()
![]()
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)若![]() 的取值范围.
的取值范围.
17. ( 本小题满分12分)
在2004年雅典奥运会上,中国女排与俄罗斯女排以“五局三胜制”进行决赛,根据以往战况,中国女排在每一局中赢的概率都是![]() ,若比赛中,俄罗斯女排先胜了第一局。求:
,若比赛中,俄罗斯女排先胜了第一局。求:
(1) 中国女排在这种情况下取胜的概率;
(2) 设比赛局数为![]() ,求P(
,求P(![]() =4).
=4).
18. (本小题满分12分)
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=![]() ,E、F 分别为AB和A1D的中点。
,E、F 分别为AB和A1D的中点。
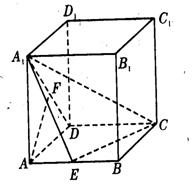 (1)求证:AF∥面A1EC;
(1)求证:AF∥面A1EC;
(2)求A1C与底面ABCD所成角的正切值;
(3)求二面角A1-EC-D的正切值。
19.(本小题满分12分)
市政府为招商引资,决定对外资企业第一年产品免税.某外资厂该年A型产品出厂价为每件60元,年销售量为11.8万件.第二年,当地政府开始对该商品征收税率为p%(0<p<100,即销售100元要征收p元)的税收,于是该产品的出厂价上升为每件![]() 元,预计年销售量将减少p万件.
元,预计年销售量将减少p万件.
(Ⅰ)将第二年政府对该商品征收的税收y(万元)表示成p的函数,并指出这个函数的定义域;
(Ⅱ)要使第二年该厂的税收不少于16万元,则税率p%的范围是多少?
(Ⅲ)在第二年该厂的税收不少于16万元的前提下,要让厂家获得最大销售金额,则p
应为多少?
20. (本小题满分13分)
在三角形ABC中,已知A(0,1), B(0,-1). AC、BC两边所在直线分别与x轴交于E、F,且![]() 。
。
(1) 求点C的轨迹方程;
(2) 若![]() ,①试确定点F的坐标;②设P是点C的轨迹上的动点,猜想△PBF的周长最大时点P的位置,并证明你的猜想。
,①试确定点F的坐标;②设P是点C的轨迹上的动点,猜想△PBF的周长最大时点P的位置,并证明你的猜想。
21. (本小题14分)
已知数列![]() ,
,![]() 是其前
是其前![]() 项的和,且
项的和,且![]() (
(![]() ≥2),
≥2),![]()
(I)求数列![]() 的通项公式;
的通项公式;
(II)设![]() ,
,![]() ,是否存在最小的正整数
,是否存在最小的正整数![]() ,使得对于任意的正整数n,有
,使得对于任意的正整数n,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
南县一中高三文科数学调研考试试卷答案
1 B 2 D 3 D 4 A 5 D 6 D 7 C 8 B 9 C 10 C
11 55 12 9 13 2 14 2 15 58000元
16解:(Ⅰ)![]() =
=![]() ·
·![]() =
=![]()
=![]() ,则
,则![]() 的最小正周期为
的最小正周期为![]() .……………6分
.……………6分
(Ⅱ)由![]() ·
·![]() <-1,得
<-1,得![]() .
.
又![]() ,则
,则![]() ,即
,即![]() .
.
故![]() 的取值范围是(
的取值范围是(![]() ).……………12分
).……………12分
17
解:(1)中国女排可能以3:1取胜,也可能以3:2取胜.
中国女排若以3:1取胜,说明第2、3、4局都取胜,其概率为:![]() ;(2分)
;(2分)
中国女排若以3:2取胜,说明第2、3、4局胜了两局,
其概率为:![]() (4分)
(4分)
![]() 中国女排取胜的概率为:
中国女排取胜的概率为:![]() (6分)
(6分)
(2)比赛局数为4包括两种情况,一是中国女排以3:1取胜,另一种是俄罗斯女排以3:1取胜若中国女排以3:1取胜,说明第2、3、4局都取胜,其概率为:![]() ;(8分)
;(8分)
若俄罗斯女排以3:1取胜,则中国女排胜了第2、3局中的一局,俄罗斯女排胜了第4局,
其概率为:![]() ,
(10分)
,
(10分)
故P(![]() =4)=
=4)= ![]() (12分)
(12分)
18
(1)在长方体AC1中,取AC1的中点O,连结OF、OE.
在△A1CD中,![]() F、O分别为A1D、A1C的中点。
F、O分别为A1D、A1C的中点。![]() FO∥DC,且FO=
FO∥DC,且FO=![]() DC。
DC。
![]() FO∥AE. 又
FO∥AE. 又![]() E为AB的中点, 且AB=DC,
E为AB的中点, 且AB=DC, ![]() FO=AE.
FO=AE.
![]() 四边形AEOF是平行四边形,
四边形AEOF是平行四边形, ![]() AF∥OE.
AF∥OE.
又OE![]() 平面A1EC, AF
平面A1EC, AF![]() 平面A1EC,
平面A1EC,![]() AF∥平面A1EC
( 4分)
AF∥平面A1EC
( 4分)
(2) 连结AC, ![]() AA1⊥平面ABCD,
AA1⊥平面ABCD, ![]() ∠ACA1是A1C与平面ABCD所成的角。
∠ACA1是A1C与平面ABCD所成的角。
在Rt△A1AC中,tan∠ACA1=![]() =
=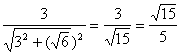 .
.
即A1C与平面ABCD所成的角的正切值为![]() . (8分)
. (8分)
(3)作AM⊥CE,交CE的延长线于M, 连结A1M, 易证A1M⊥CE.
∠A1MA是二面角A1—EC—D的平面角,
在△AME、△CBE中,易得AM=![]() ,在△A1MA中,A1A=3,tan∠AMA1=
,在△A1MA中,A1A=3,tan∠AMA1=![]() =
=![]()
![]() 二面角A1—EC—D的正切值为
二面角A1—EC—D的正切值为![]() . (12分)
. (12分)
19
(I)解:依题意,第二年该商品年销售量为(11.8-p)万件,
年销售收入为![]() (11.8-p)万元,…………………………2分
(11.8-p)万元,…………………………2分
政府对该商品征收的税收y=![]() (11.8-p)p%(万元)
(11.8-p)p%(万元)
故所求函数为y=![]() (11.8-p)p……………………………………4分
(11.8-p)p……………………………………4分
由11.8-p>0及p>0得定义域为0<p<11.8…………………………5分
(II)解:由y≥16得![]() (11.8-p)p≥16
(11.8-p)p≥16
化简得p2-12p+20≤0,即(p-2)(p-10) ≤0,解得2≤p≤10.………………7分
故当税率在[0.02,0.1]内时,税收不少于16万元.……………………8分
(III)解:第二年,当税收不少于16万元时,
厂家的销售收入为g(p)= ![]() (11.8-p)(2≤p≤10)
(11.8-p)(2≤p≤10)
![]() 在[2,10]是减函数……10分
在[2,10]是减函数……10分
∴g(p)max=g(2)=800(万元)………………………………………………11分
故当税率为2%时,厂家销售金额最大.………………………………12分
20
(1)如图,设点C(x,y)(x![]() ,E(xE,0), F(xF,0).
,E(xE,0), F(xF,0).
由A、B、E三点共线,![]() //
//![]() ,
,![]() x(-1)-(y-1)xE=0, 解得
x(-1)-(y-1)xE=0, 解得![]() ,
,
同理由B、C、F三点共线,
解得![]() ,
(2分)
,
(2分)
![]()
![]() ,
,![]()
![]()
![]()
![]() =4
=4
化简得![]() ( 4分)
( 4分)
(2)若![]() ,
,
①设F(xF,0) ,C(xC,yC)
由![]() 得
得![]() =
=![]()
![]()
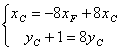
![]()
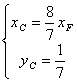 ( 6分)
( 6分)
代入![]() 得
得![]() ,
,![]() xF=
xF=![]() ,
,
![]() 点F(
点F(![]() ,0)即为椭圆的焦点。 ( 8分)
,0)即为椭圆的焦点。 ( 8分)
②猜想:设F(![]() ,则当点P位于直线BF1与椭圆C的交点处时,△PBF周长最大为8。
(9分)
,则当点P位于直线BF1与椭圆C的交点处时,△PBF周长最大为8。
(9分)
证明如下:PF+PB=4-PF1+PB=4+(PB-PF1)![]() 4+BF1,
4+BF1,
![]() △PBF的周长
△PBF的周长![]() 4+BF1+BF=8. (13分)
4+BF1+BF=8. (13分)
21
(I)由已知![]() ①
① ![]() ②
②
②-①,得![]() (
(![]() ≥2)
2分
≥2)
2分
∴![]() ,又
,又![]() ,所以数列
,所以数列![]() 是一个以2为首项,8为公比的等比数列
是一个以2为首项,8为公比的等比数列
∴![]() 4分
4分
(II)![]() 5分
5分
∴![]()
![]()
∴![]() 7分
7分
![]()
∵![]() ,∴
,∴![]() ≥1,即
≥1,即![]()
∴![]() ,
,![]() ,即数列
,即数列![]() 是一个单调递减数列,又
是一个单调递减数列,又![]()
∴![]() ≤
≤![]() ,若
,若![]() 恒成立,则
恒成立,则![]() ,即
,即![]() 13分
13分
又![]() 是正整数,故最小正整数
是正整数,故最小正整数![]() 为4
为4
14分