惠州市2007届高三模拟考试
数学试题(文科卷)(2007.4)
本试卷分为第I卷(选择题)和第Ⅱ卷(非选择题),共4页.全卷满分150分,考试时间120分钟.
第Ⅰ卷(选择题 共50分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.不能答在试题卷上.
3.本卷共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
一.选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 设全集U=Z,集合M=![]() ,P=
,P=![]() ,则P
,则P![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 一枚硬币连掷2次,只有一次出现正面的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 已知直线a、b、c和平面M,则a//b的一个充分条件是( ).
A.a//M ,b//M B. a![]() c ,b
c ,b![]() c
c
C.a、b与平面M成等角 D.a![]() M ,b
M ,b![]() M.
M.
5. 已知实数![]() 满足约束条件
满足约束条件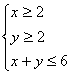 ,则
,则![]() 的最大值为( ).
的最大值为( ).
A.24 B.20 C.16 D.12
6.在数列{![]() }中,若
}中,若![]() 且对所有
且对所有![]() , 满足
, 满足![]() ,则
,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
7.下列算法中,含有条件分支结构的是( )
A.求两个数的积 B.求点到直线的距离
C.解一元二次不等式 D.已知梯形两底和高求面积
8.已知向量![]() ,且
,且![]() ,则向量
,则向量![]() 与
与![]() 的夹角为( )
的夹角为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数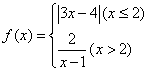 ,则
,则![]() 的自变量
的自变量![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.![]() 为圆
为圆![]() 内异于圆心的一点,则直线
内异于圆心的一点,则直线![]() 与该圆的位置关系为( )
与该圆的位置关系为( )
A.相离 B.相交 C.相切 D.相切或相离
二.填空题(本大题共4小题,每小题5分,共20分.)
11.函数![]() 的图象中相邻两条对称轴的距离为______________________________.
的图象中相邻两条对称轴的距离为______________________________.
12.已知双曲线的方程为![]() ,则它的离心率e =_______________________.
,则它的离心率e =_______________________.
|
【选做题】从14、15题中选做1题,多做只计14题得分!!
14. 如图所示,在△ABC中,AD是高线,![]() 是中线,
是中线,
DC=BE, DG![]() CE于G, EC的长为8,
CE于G, EC的长为8,
则EG=__________________.
15直线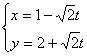 (t为参数)上到点A(1,2)的
(t为参数)上到点A(1,2)的
距离为4![]() 的点的坐标为_____________________________.
的点的坐标为_____________________________.
三.解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤).
16.(本小题满分12分)
在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() ,判断△ABC的形状.
,判断△ABC的形状.
17.(本小题满分12分)
已知等差数列{![]() },
},![]() .
.
(1).求![]() 的通项公式;
的通项公式;
(2).令![]() ,求数列的前项和.
,求数列的前项和.
18.(本小题满分14分)
甲乙二人用4张扑克牌(分别是红桃2 红桃3 红桃4 方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1).设![]() 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况.
(2).若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3).甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜.你认为此游戏是否公平,说明你的理由.
19.(本小题满分14分)
如图ABCD是正方形,O是正方形的中心,PO![]() 底面 ABCD,E是PC的中点.
底面 ABCD,E是PC的中点.
求证:(1).PA//平面BDE;
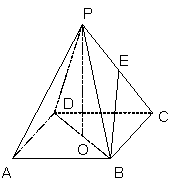 (2).平面PAC
(2).平面PAC![]() 平面BDE.
平面BDE.
20.(本小题满分14分)
已知中心在原点,焦点在坐标轴上的椭圆过![]() ,
,![]() 两点。
两点。
(1).求椭圆的离心率;
(2).在椭圆上是否存在点![]() 到定点
到定点![]() (其中
(其中![]() )的距离的最小值为1,若存在,求出
)的距离的最小值为1,若存在,求出![]() 的值及点
的值及点![]() 的坐标;若不存在,请给予证明.
的坐标;若不存在,请给予证明.
21.(本小题满分14分)
设![]() 是定义在R上的奇函数,
是定义在R上的奇函数,![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称,若
对称,若![]() .
.
⑴.求![]() 的解析式;
的解析式;
⑵.当x=1时,![]() 取得极值,证明:对任意
取得极值,证明:对任意![]() ,不等式
,不等式![]() 恒成立;
恒成立;
⑶.若![]() 是[1,+
是[1,+![]() )上的单调函数,且当
)上的单调函数,且当![]() ,
,![]() 时,有
时,有![]() ,
,
求证:![]() .
.
惠州市2007届高三模拟考试
数学试题(文科卷)(2007.4)答案
一.选择题(本大题共10小题,每小题5分,共50分)
1.D本题主要考察互为共轭复数的概念及复数的乘法运算.
Z=1+![]() ,
,![]() ,
,![]() ,故选 D.
,故选 D.
2.C
本题主要考察含绝对值不等式的解法及集合间的运算交与补.集合P=![]() ,M=
,M=![]() ,
,![]() =
=![]() ,
,![]() P
P![]()
![]() =
=![]() .故选C.
.故选C.
3.D
本题主要考察的是古典概型,一枚硬币连掷2次可能出现正正,反反,正反,反正四种情况,而只有一次出现正面的有两种,![]() P=
P=![]() =
=![]() 故选D.
故选D.
4.C 本题主要考察立体几种线线,线面的位置关系.A是a//b的充分条件B是a//b的充分必要条件,C是a//b的充分条件.D是a//b的必要不充分条件.故选C
5.B 本题主要考察的是简单的线性规划问题.目标函数在点(2,4)处取得最大值20故选B
6.B
本题主要考察数列由递推公式求通项或代入法求值.![]()
![]()
![]() ,
,![]() ,
,![]() ,故选B.此题也可求
,故选B.此题也可求![]() ,
,![]() ,
,![]() ,
,![]() .
.
7.C 本题主要考察的是算法中条件分支问题,A、B、D不含条件分支,解一元二次不等式要用到条件分支故选C.
8.B 本题主要考察向量的数量积及三角函数和值求角.由![]() =
=![]()
![]() cos
cos![]() =
=![]() ,
,
故![]() ,选B.
,选B.
9.D 本题主要考察分式,绝对值不等式的解法.
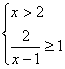 或
或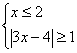
![]()
![]() 或
或![]() 或
或![]()
![]()
![]() 或
或![]() 选D.
选D.
10.A
本题主要考察点与圆的位置关系及直线与圆的位置关系.点M在圆内故![]() ,圆心到直线的距离
,圆心到直线的距离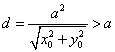 .故直线与圆相离.选A.
.故直线与圆相离.选A.
二.填空题(本大题共4小题,每小题5分,共20分.)
11.![]() 本题主要考察正弦函数图像,相邻对称轴间的距离为半个周期,故此题关键是求函数的周期.T=
本题主要考察正弦函数图像,相邻对称轴间的距离为半个周期,故此题关键是求函数的周期.T=![]() =
=![]() .
.
12.![]() ,
,![]() . 此题考察的是双曲线的基本概念.由于此题没有说明焦点的位置,因此要分类讨论.当焦点在
. 此题考察的是双曲线的基本概念.由于此题没有说明焦点的位置,因此要分类讨论.当焦点在![]() 轴时
轴时![]() ;当焦点在
;当焦点在![]() 轴时
轴时 ![]() .
.
13.[0,1] 此题考察导数的应用以及解一元二次不等式.![]()
![]()
![]() .
.
14.4
考查直角三角形中的中线的性质及等腰三角形底边中线的性质.连接DE,则DE=![]() AB=BE=DC.
AB=BE=DC.
∴DG平分EC,故EG=4.
15.(-3,6)或(5,-2)考查的是直线的参数方程问题.点![]() 为直线上的点
为直线上的点
![]() ,解得
,解得![]() 或
或![]() ,
,
故P(-3,6)或(5,-2).
三.解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤).
16.(本小题满分12分)
解.(1)由已知得.![]() ,
…………………………………… (3分)
,
…………………………………… (3分)
又![]() 是△ABC的内角,所以
是△ABC的内角,所以![]() . …………………………………………… (6分)
. …………………………………………… (6分)
(2)(方法一)由正弦定理得.![]() , …………………………………………………… (7分)
, …………………………………………………… (7分)
又 ![]() ,
,
∴ ![]() ,
…………………………………………………………………… (9分)
,
…………………………………………………………………… (9分)
∴ ![]() ,即
,即 ![]() . ……………………………………………………………… (10分)
. ……………………………………………………………… (10分)
所以△ABC是等边三角形. ………………………………………………………………… (12分)
(方法二)![]() , ………………………………… (7分)
, ………………………………… (7分)
又 ![]() ,
,
∴ ![]() , ……………………………………………………… (8分)
, ……………………………………………………… (8分)
![]() ,又
,又 ![]() , ……………………………………………………… (9分)
, ……………………………………………………… (9分)
∴ ![]() ,即
,即![]() , ……………………………………………………………… (10分)
, ……………………………………………………………… (10分)
所以△ABC是等边三角形. ……………………………………………………………… (12分)
17.(本小题满分12分)解.(1) ![]() ,∴
,∴![]() , ………………… (3分)
, ………………… (3分)
![]() ,
……………………… (6分)
,
……………………… (6分)
(2) ∵![]() ,∴
,∴![]() ,
……………………… (9分)
,
……………………… (9分)
∴![]() ……… (12分)
……… (12分)
18.(本小题满分14分) 解:(1)甲乙二人抽到的牌的所有情况(方片4用4 ’表示)为:
(2,3)、(2,4)、(2,4 ’)、(3,2)、(3,4)、(3,4 ’)、
(4,2)、(4,3)、(4,4 ’)、( 4 ’,2)、(4 ’,3)(4 ’,4),共12种不同情况.……… (5分)
(没有写全面时:只写出1个不给分,2—4个给1分,5—8个给2分,9—11个给3分)
(2)甲抽到3,乙抽到的牌只能是2,4,4.因此乙抽到的牌的数字大于3的概率为![]() ;…… (9分)
;…… (9分)
(3)由甲抽到牌比乙大有(3,2)、(4,2)、(4,3)、(4 ’,2)、(4 ’,3)5种, ………… (11分)
甲胜的概率![]() ,乙获胜的概率为
,乙获胜的概率为![]() .∵
.∵![]() <
<![]() ,∴此游戏不公平.………… (14分)
,∴此游戏不公平.………… (14分)
19.(本小题满分14分)证:
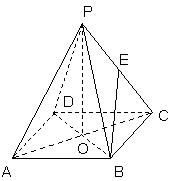 (1) 连接AC、OE,AC
(1) 连接AC、OE,AC![]() BD=O,
…………
(1分)
BD=O,
…………
(1分)
在△PAC中,∵E为PC中点,O为AC中点.∴PA // EO,…… (3分)
又∵EO ![]() 平面EBD ,PA
平面EBD ,PA ![]() 平面EBD,∴PA
//BDE.…………
(7分)
平面EBD,∴PA
//BDE.…………
(7分)
(2)∵PO![]() 底面ABCD,∴PO
底面ABCD,∴PO![]() BD.
…………
(9分)
BD.
…………
(9分)
又∵BD![]() AC,∴BD
AC,∴BD![]() 平面PAC.
…………
(12分)
平面PAC.
…………
(12分)
又BD![]() 平面BDE,∴平面PAC
平面BDE,∴平面PAC![]() 平面BDE. ………… (14分)
平面BDE. ………… (14分)
20.(本小题满分14分)
解:(1)设椭圆方程为![]() ……………………… (2分)
……………………… (2分)
![]() 椭圆过M,N两点,∴
椭圆过M,N两点,∴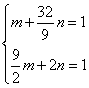 ……………………… (3分)
……………………… (3分)
![]()
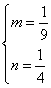 ……………………… (4分)
……………………… (4分)
![]() 椭圆方程为
椭圆方程为![]() ﹒故椭圆的离心率为
﹒故椭圆的离心率为![]() . ……………………… (6分)
. ……………………… (6分)
(2)设存在点P![]() 满足题设条件,∴
满足题设条件,∴![]() =
=![]()
又![]()
![]()
![]() =
=![]() ,
,
∴![]() =
=![]()
![]() =
=![]() , ……………………… (8分)
, ……………………… (8分)
当![]() 即
即![]() ,
,![]() 的最小值为
的最小值为 ![]() 依题意,
依题意,
![]() ,
……………………… (10分)
,
……………………… (10分)
∴![]() 即
即![]() ,此时
,此时![]() ,
……………………… (11分)
,
……………………… (11分)
![]() 的最小值为
的最小值为![]() .依题意
.依题意![]() ,∴
,∴![]() ,此时点P的坐标是
,此时点P的坐标是![]() .……… (13分)
.……… (13分)
故当![]() 时,存在这样的点
时,存在这样的点![]() 满足条件,
满足条件,![]() 点的坐标是
点的坐标是![]() . ……………………… (14分)
. ……………………… (14分)
21.(本小题满分14分) 解:(1)![]()
![]() 与
与![]() 的图象关于
的图象关于![]() 对称,
对称,
设点![]() 是
是![]() 上的任意一点.则点
上的任意一点.则点![]() 关于
关于![]() 的对称点
的对称点![]() 在函数
在函数![]() 的图象上.∴
的图象上.∴![]()
![]()
![]() . ……………………… (2分)
. ……………………… (2分)
(2)![]() =
=![]() ,又
,又![]() 是函数
是函数![]() 的一个极值点,
的一个极值点,
∴![]() ,得
,得![]() , ……………………… (3分)
, ……………………… (3分)
故![]() .
.![]() ,当
,当![]() ,
,![]() ,
,
∴![]() 在
在![]() 上是减函数. ……………………… (4分)
上是减函数. ……………………… (4分)
![]() ,
,![]() , ……………………… (5分)
, ……………………… (5分)
故对任意![]() ,有
,有![]() . ……………………… (6分)
. ……………………… (6分)
(3)若![]() 在
在![]() 是减函数,则
是减函数,则![]() 在
在![]() 上恒成立.
上恒成立.
即![]() 在
在![]() 上恒成立,此时
上恒成立,此时![]() 不存在; ……………………… (8分)
不存在; ……………………… (8分)
若![]() 在
在![]() 是增函数,即
是增函数,即![]() 在
在![]() 上恒成立.故
上恒成立.故![]() . …………… (10分)
. …………… (10分)
设![]() 则
则![]() ,∴
,∴![]() 矛盾, ……………………… (12分)
矛盾, ……………………… (12分)
若![]() 则
则![]() ∴
∴![]() 矛盾!
矛盾!
故![]() .
……………………… (14分)
.
……………………… (14分)