西安中学2007年3月份月考高三理科数学试题答案
一、选择题(每小题5分,共计60分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | A | B | C | C | D | A | C | B | B | A | D |
二、填空题:(每小题4分,共计16分)
13、 5 ; 5
14、 -3或-13 15、
![]() 16、
16、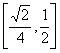
三.解答题:(本大题共6个小题,共74分.解答应写出文字说明、证明过程或演算步骤)
17、(本大题满分12分)
解:(1)由题意得:![]() ,
,![]() ,
,![]() ,
,![]()
(2)由(1)及条件得![]()
![]() ,
,![]() ;∴当
;∴当![]() 时,
时,![]() 取得最大值,最大值为2
取得最大值,最大值为2
18. (本大题满分12分)
解:(Ⅰ)记“甲连续射击4次,至少1次未击中目标”为事件A1,由题意,射击4次,相当于4次独立重复试验,故P(A1)=1- P(![]() )=1-
)=1-![]() =
=![]()
![]()
答:甲射击4次,至少1次未击中目标的概率为![]() ;
;
(Ⅱ) 记“乙恰好射击5次后,被中止射击”为事件A3,“乙第i次射击为击中” 为事件Di,(i=1,2,3,4,5),则A3=D5D4![]() ,且P(Di)=
,且P(Di)=![]() ,由于各事件相互独立,
,由于各事件相互独立,
故P(A3)= P(D5)P(D4)P(![]() )=
)=![]() ×
×![]() ×
×![]() ×(1-
×(1-![]() ×
×![]() )=
)=![]() ,
,
答:乙恰好射击5次后,被中止射击的概率是![]()
![]()
(Ⅲ)根据题意ξ服从二项分布;Eξ=5×![]() =
=![]()
19、(本小题满分12分)
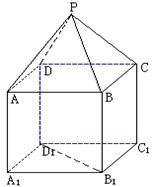 解法一:以
解法一:以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系
(1)设E是BD的中点,![]() P—ABCD是正四棱锥,∴
P—ABCD是正四棱锥,∴![]()
又![]() , ∴
, ∴![]() ∴
∴![]()
∴ ![]()
∴ ![]() 即
即![]() ………4分
………4分
(2)设平面PAD的法向量是![]() ,
, ![]()
∴ ![]() 取
取![]() 得
得![]() , 又平面
, 又平面![]() 的法向量是
的法向量是![]()
∴ 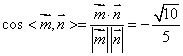 ∴
∴![]() ………8分
………8分
(3)![]() ∴
∴![]() 到平面PAD的距离
到平面PAD的距离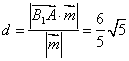 ……12分
……12分
解法二:(1)设AC与BD交点为O,连AO,PO;∵P—ABCD是正四棱锥,∴PO⊥面ABCD,
∴AO为PA在平面ABCD上的射影, 又ABCD为正方形,∴AO⊥BD,由三垂线定理知
PA⊥BD,而BD∥B1D1;∴![]() ………4分
………4分
(2)由题意知平面PAD与平面![]() 所成的锐二面角为二面角A-PD-B;
所成的锐二面角为二面角A-PD-B;
∵AO⊥面PBD,过O作OE垂直PD于E,连AE,则由三垂线定理知∠AEO为二面角A-PD-B的平面角;可以计算得,![]()
(3)设B1C1与BC的中点分别为M、N;则![]() 到平面PAD的距离为M到平面PAD的距离;
到平面PAD的距离为M到平面PAD的距离;
由VM-PAD=VP-ADM求得![]() ;或者d为M点到直线PK的距离(K为D的中点);
;或者d为M点到直线PK的距离(K为D的中点);
20、(本小题满分12分)
解:(1)∵![]() ,∴
,∴![]() =
=![]() =
=![]()
令![]() ,得
,得![]() =2,
=2,![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
∴在区间![]() 上,
上,![]() =2时,
=2时,![]() 最大=
最大=![]() ;
;
![]() ;而
;而![]() ,
,![]() =
=![]()
![]()
![]()
∴![]()
![]()
(2)∵![]() ,∴
,∴![]() =
=![]()
①当![]() 时,由
时,由![]() 得:
得:![]() 0,由
0,由![]() 得:
得:![]() 0,又
0,又![]()
∴![]() 在
在![]() 为增函数
为增函数
②当![]() 时,
时,![]() =
=![]() =
=![]()
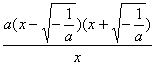
由![]() 得:
得: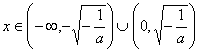
由![]() 得:
得: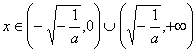 又
又![]()
∴![]() 的单调增区间,
的单调增区间,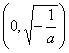 ;减区间
;减区间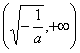
21、(本小题满分12分):解:(I)![]() ∴NP为AM的垂直平分线,∴NA=NM
∴NP为AM的垂直平分线,∴NA=NM![]() 又
又![]()
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆![]()
且椭圆长轴长为![]() 焦距2c=2
焦距2c=2![]()
![]()
∴曲线E的方程为![]()
(II)当直线GH斜率存在时,
设直线GH方程为![]()
得![]()
设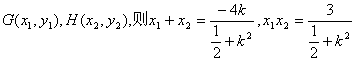
![]()
![]() ,
,
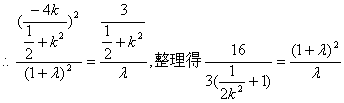
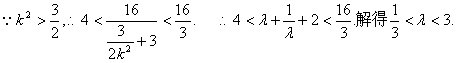
![]()
又当直线GH斜率不存在,方程为![]()
![]()
22.(本小题满分14分)
解:(1)令![]() ,
,![]() ,得
,得![]() ,
,![]() ,故
,故![]()
![]()
当![]() 时,
时,![]() ,
,![]() ,进而得
,进而得![]()
![]()
设![]() R,且
R,且![]() ,
,
则![]() ,
,![]() ,
,![]()
![]()
![]()
故![]() ,函数
,函数![]() 在R上是单调递减函数
在R上是单调递减函数![]()
(2)由![]() ,得
,得![]()
![]()
故![]() ,
,![]() ,
,![]() (
(![]() N)
N)
因此,![]() 是首项为1,公差为2的等差数列
是首项为1,公差为2的等差数列![]() 由此得
由此得![]() ,
, ![]()
![]()
(3) 由![]() 恒成立,
恒成立,
知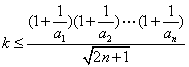 恒成立
恒成立![]()
设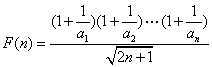 ,则
,则![]() ,
,
且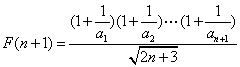
![]()
又![]() ,即
,即![]() ,故
,故![]() 为关于
为关于![]() 的单调增函数,
的单调增函数,![]()
![]() 所以,
所以,![]() ,即
,即![]() 的最大值为
的最大值为![]()
![]()