高三理科数学模拟试题

祁阳四中高三理科数学试题(2007-3)

一.选择题（每小题5分，共50分）

1、已知为虚数单位，则（　　）

A、　　　　  B、　　　　　 C、　　  D、

2、已知函数（　 ）

　A、　　　　　　 B、　　　　　  C、　　　　  D、

3、若的最小值是（　　）

A、　　　　　 B、　　　　　　C、　　　　D、

4、若O是△ABC所在平面内一点，且满足，则

△ABC的形状为（　　）

A、等腰直角三角形　　　　　　 B、直角三角形　　

C、等腰三角形　　　　　　　　 D、等边三角形

5、表面积为 的正八面体的各个顶点都在同一个球面上，则此球的体积为（　　）

 A．　　　　　  B．　　　　　 C．　　　　　  D．

6、已知圆C：，直线 圆上存在两点到直线l的距离为1，则k的取值范围是　　　　　　　 （　　）　　　　　　　　　　　　　　　　　　　　　　　

　　　 A．（－17，－7）　　　　　　　　　　　　　　　　B．（3，13）　　　　

　　　 C．（－17，－7）∪（3，13）　　　　　D．[－17，－7]∪[3，13]

7、对于R上可导的任意函数f（x），若满足（x－1）³0，则必有（  ）

　　A、f（0）＋f（2）<2f（1）　　　 B. f（0）＋f（2）£2f（1）

C、f（0）＋f（2）³2f（1）　　　 D. f（0）＋f（2）>2f（1）

8、某公路上竖立着6块广告牌，底色只能用红色、绿色中的一种，则相邻两块广告牌的底色不同为绿色的配色方案有（　　）种。

A、15　　　　　　　  B、21　　　　　　 C、18　　　　　　 D、20

9、设数列的前的“理想数”，已知数列的“理想数”为2004，那么数列的“理想数”为（　 ）

A、2007　　　　　　  B、2004　　　　　  C、2002　 　　　　　 D、2008

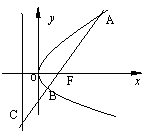
10、如图，过抛物线的焦点F的直线交抛物线于点A、B，交其准线于点C，若，且，则此抛物线的方程为　(　　)　　　　　　　　　　 

　　　 A．　　　　　 　　　 B．　　

　　C．　 　　 　　　 D．　　　　　　　　　　　　　　　　 

二.填空题（每小题5分，共25分）

11、若 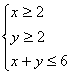，则目标函数的取值范围是　　　　　

12、的展开式中，常数项为______。

13、如果且函数为奇函数，的导函数，则=_______.

14、已知函数，若在区间[1，＋∞上是增函数，则实数a的取值范围是　　　　　　  .

15、已知点，其中n为正整数。设S_n表示△ABC外接圆的面积，则＝___________。

祁阳四中高三理科数学试题答卷（2007-3）

班次　　 学号　　  姓名　　　　　　 

一.选择题（每小题5分，共50分）

题号	1	2	3	4	5	6	7	8	9	10
答案

二.填空题（每小题5分，共25分）

11.____________；　12._________ ；13.____________；　 

14．___________；　15．____________。

三.解答题（12′+12′+12′+12′+13′+14′=75′）

16．已知是三角形三内角，向量，且

　 （Ⅰ）求角；（Ⅱ）若，求的值.

17、一种电路控制器在出厂时每4件一等品装成一箱，工人在装箱时不小心把2件二等品和2件一等品装入了一箱，为了找出该箱中的二等品，我们对该箱中的产品逐一取出进行测试0

（1）求前两次取出的都是二等品的概率；

（2）用随机变量表示第二个二等品被取出时共取出的件数，求的分布列及期望.

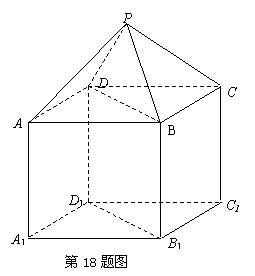18．如图，是正四棱锥,是正方体，其中．

（Ⅰ）求证：；

（Ⅱ）求平面与平面所成的

锐二面角的大小；

（Ⅲ）求到平面的距离．

19．已知函数，数列满足，

　 （1）求数列的通项公式；

　 （2）若数列满足，求。

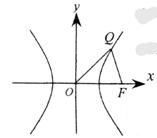20、已知△OFQ的面积为，

（1）设，求向量的取值范围；

（2）设以O为中心，F为焦点的双曲线经过点Q（如图），

若，取最小值时，求此双曲线的方程。

21．如果在某个区间I内满足：

对任意的，则称在I上为下凸函数；已知函数

　 （Ⅰ）证明：当时，在上为下凸函数；

　 （Ⅱ）若为的导函数，且时，求实数a的取值范围.

祁阳四中高三理科数学试题参考答案(2007.3)

一.选择题

题号	1	2	3	4	5	6	7	8	9	10
答案	B	B	C	B	A	C	C	B	C	D

二.填空题

11. 　　 12. 180　　 13. 　　 14. 　　　　15.

16．解：（Ⅰ）∵，∴，∴，，

　　　　 ∵，∴，∴，∴

　 （Ⅱ）∵，∴由正弦定理得,　

　　∵　 ∴，

　　即

17、解：（1）四件产品逐一取出排成一列共有A⁴₄种方法，前两次取出的产品都是二等品的共有A²₂×A²₂种方法，

∴前两次取出的产品都是二等品的概率为

　 （2）的所有可能取值为2、3、4，

∴的概率分布为：

2 3 4 P

　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　　　

∴E=

18．解：(Ⅰ) 连结AC , 交BD于点O , 连结PO , 则PO⊥面ABCD , 又∵ , ∴, ∵, ∴ ．

 （Ⅱ） ∵AO⊥BD , AO⊥PO , ∴AO⊥面PBD , 过点O作OM⊥PD于点M，连结AM , 则AM⊥PD ,　 ∴∠AMO 就是二面角A-PD-O的平面角,

又∵, ∴AO=,PO=

 , ∴ ,

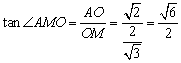即二面角的大小为 ．　　　　　　　　　　　　　

 (Ⅲ)用体积法求解：即有

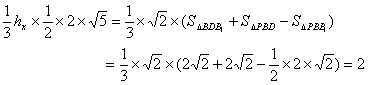
解得，

即到平面PAD的距离为

19、解：（1）

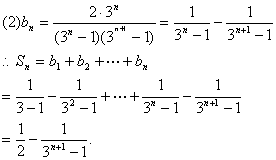
20．（1）由已知，得，∴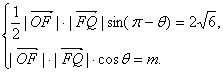

　　　　∴

（2）设所求的双曲线方程为

∵△OFQ的面积，∴

又由，∴

此时Q的坐标为　由此可得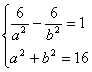

解得

21、解（Ⅰ）任取

则

又

又

即.

下凸函数.

　 （Ⅱ），

恒成立. .