2007届高三理科数学模拟题
武穴中学
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.若![]() ,则n等于( )
,则n等于( )
A.4 B.5 C.6 D.7
2.一个球的直径为6,则此球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:(1)
是不同的平面,有以下四个命题:(1)![]()
(2)![]() (3)
(3)![]() (4)
(4)![]() ,其中,假命题是
,其中,假命题是
A、(1)(2) B、(2)(3) C、(1)(3) D、(2)(4)
4.已知空间向量![]() (1,0),
(1,0),![]() (2,k),
(2,k),![]() ,则k的值为( )
,则k的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知直线![]() 是函数
是函数![]() 图象的一条对称轴,则函数
图象的一条对称轴,则函数![]() 图象的一条对称轴方程是
图象的一条对称轴方程是
A、![]() B、
B、![]() C、
C、![]() D、
D、
6.曲线y = 2x3 + x,在点P(1,a)处的切线方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知等差数列![]() 的前
的前![]() 项的和为
项的和为![]() ,且
,且![]() ,
,![]() ,则过点
,则过点![]() 和
和![]() 的直线的一个方向向量的坐标是
的直线的一个方向向量的坐标是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8.函数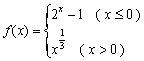 ,则不等式
,则不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
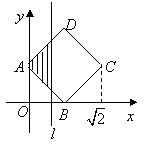 9.若如图,正方形
9.若如图,正方形![]() 的顶点
的顶点![]() ,
,![]() ,顶点
,顶点![]() 位于第一象限,直线
位于第一象限,直线![]() 将正方形
将正方形![]() 分成两部分,记位于直线
分成两部分,记位于直线![]() 左侧阴影部分的面积为
左侧阴影部分的面积为![]() ,则函数
,则函数![]() 的图象大致是
的图象大致是
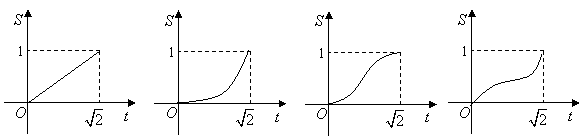 |
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10.极限![]() 的值为( )
的值为( )
A.2 B.1 C.![]() D.0
D.0
第Ⅱ部分 (非选择题,共100分)
二、填空题:本大题共6小题,每小题4分,共24分.把答案填写在答题卡相应位置上.
11.直线![]() 交于A、B两点,点A(2,1),设抛物线的焦点为F,则
交于A、B两点,点A(2,1),设抛物线的焦点为F,则![]() _______________.
_______________.
12.已知点P(x,y)在曲线![]() 上运动,作PM垂直x轴于M,则△POM(O为坐标原点)的周长的最小值为______________.
上运动,作PM垂直x轴于M,则△POM(O为坐标原点)的周长的最小值为______________.
13. 从某社区65户高收入家庭,280户中等收入家庭,105户低收入家庭中选出100户调查社会购买力的某一项指标,应采用的最佳抽样方法是______________.
14.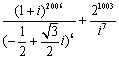 的值等于________________.
的值等于________________.
15.用5种颜色将一个正五棱锥的各面涂色,五个侧面分别编有1、2、3、4、5号,而有公共边的两个面不能涂同一种颜色,则不同的涂色的方法数为________________.
三、解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤
16、已知函数![]()
(1)求![]() 的单调增区间
的单调增区间
(2)在直角坐标系中画出函数![]() 在区间
在区间![]() 上的图象。
上的图象。
17.(1)某车场有一排16个停车位,现要停12辆汽车,求:事件“恰有四个空位连在一起发生的概率.
(2)从5男4女中选3位代表去参观学习,求3个代表中至少有一个女同志的概率.
(均用数字作答)
18、已知函数![]() ,设
,设![]() ,
,![]()
![]()
(1)求![]() ,
,![]() 的表达式,并猜想
的表达式,并猜想![]()
![]() 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
(2)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上的最小值为6,求
上的最小值为6,求![]() 的值。
的值。
(符号“![]() ”表示求和,例如:
”表示求和,例如:![]() 。)
。)
19、如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 折到点
折到点![]() 的位置,且二面角
的位置,且二面角![]() 的大小为
的大小为![]()
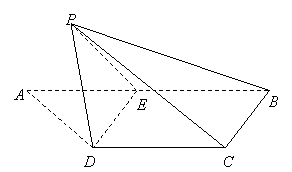 (1)求证:
(1)求证:![]()
(2)求直线![]() 与平面
与平面![]() 所成角的大小
所成角的大小
(3)求点![]() 到平面
到平面![]() 的距离
的距离
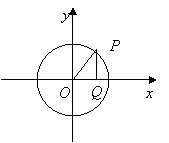 20、已知点
20、已知点![]() 是圆
是圆![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]()
(1)求点![]() 的轨迹方程
的轨迹方程
(2)求向量![]() 和
和![]() 夹角的最大值,并求此时
夹角的最大值,并求此时![]() 点的坐标
点的坐标
(3)判断函数![]() 的单调性,并用单调性的定义证明你的结论。
的单调性,并用单调性的定义证明你的结论。
21.设x1、x2是函数![]() 的两个极值点.
的两个极值点.
(1)若![]() ,求证:
,求证:![]() ;
;
(2)如果![]() ,求b的取值范围;
,求b的取值范围;
(3)如果![]() 时,求函数
时,求函数![]() 的最大值h(a).
的最大值h(a).
数学试题参考答案(理科)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.C 2.B 3.D 4.C 5.B 6.B 7.B 8.A 9.C 10.D
二、填空题:本大题共6小题,每小题5分,共25分.
11.7 12.![]() 13.分层抽样
13.分层抽样
14.0 15.1200
三、解答题:本大题共6小题,共76分,解答应写出文字说明、证明过程或演算步骤.
16.![]()
![]()
![]() 函数
函数![]() 的单调增区间为
的单调增区间为![]()
(2)图象(略)
17.解:(1) 16个停车位停12辆车有![]() 种························································ 2分
种························································ 2分
而发生四个空位连在一起的情况数为m = 13种············································· 2分
故所求的概率![]() ········································································· 2分
········································································· 2分
(2) 从9人中选三位代表有![]() 种·································································· 2分
种·································································· 2分
而至少有一位女同志有![]() 种····································· 3分
种····································· 3分
故所求概率![]() ······································· 2分
······································· 2分
18.(1)![]() ,
,![]()
![]() ,
,![]() 猜想
猜想![]()
(2)![]() ,
,![]()
![]()
(A)当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数
上是减函数
![]() 当
当![]() 时,
时,![]() ,即
,即![]() ,该方程没有整数解
,该方程没有整数解
(B)当![]() ,即
,即![]() 时,
时,![]() ,解得
,解得![]() ,综上所述,
,综上所述,![]()
19、(1)连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,即
,即![]() 平分
平分![]() ,
,![]() 是正三角形,
是正三角形,
![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]()
(2)过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角。
所成的角。
![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() ,在
,在![]() 中,
中,
![]() ,
,![]() 直线
直线![]() 与平面
与平面![]() 所成角是
所成角是![]()
(3)![]() ,
,![]() 在平面
在平面![]() 外,
外,![]() ,
,![]() 点到面
点到面![]() 的距离即为点
的距离即为点![]() 到面
到面![]() 的距离,过点
的距离,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() 的长即为点
的长即为点![]() 到面
到面![]() 的距离,菱形
的距离,菱形![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
20、解:(1)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]()
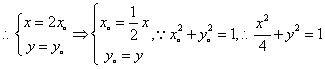
(2)设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则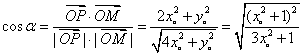
令![]() ,则
,则![]()
当且仅当![]() 时,即
时,即![]() 点坐标为
点坐标为![]() 时,等号成立。
时,等号成立。
![]() 与
与![]() 夹角的最大值是
夹角的最大值是![]()
21.解:由已知:![]() ········································································ 1分
········································································ 1分
故![]() 的两根········································································· 1分
的两根········································································· 1分
(1) 由于![]() 由于
由于![]()
·················································································································· 1分
①×(– 3)+②得:4a –
2b > 0 ∴ ![]() ······································· 1分
······································· 1分
(2) 由韦达定理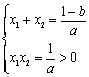
故![]() ················································ 1分
················································ 1分
当![]()
这时,由![]()
即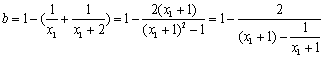 为增函数(也可用求导法来证),故
为增函数(也可用求导法来证),故![]() ···················································································································· 2分
···················································································································· 2分
当![]() 也为增函数
也为增函数
故这时,![]() ·································································· 1分
·································································· 1分
综上,b的取值范围是![]() ······················································ 1分
······················································ 1分
(3) ∵ ![]()
∴ ![]() ······································· 1分
······································· 1分
∵ ![]() ∴
∴ ![]()
∴ 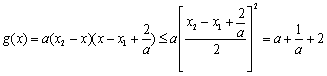 ····························· 1分
····························· 1分
当且仅当![]() 等号成立
等号成立
∴ ![]()