上海市进才中学2007届高三理科月考六数学试题
一、填空题(满分48分,每小题4分)
1.在直角坐标系中,直线![]() 的倾斜角是_______________。
的倾斜角是_______________。
2.若复数![]() ,则
,则![]() ________。
________。
3.在长方体![]() 中,若
中,若![]() ,则点
,则点![]() 到平面
到平面![]() 的距离为 ___________。
的距离为 ___________。
4.已知向量![]() ,若
,若![]() 三点共线,则
三点共线,则![]() __________。
__________。
5.椭圆![]() 的两个焦点的坐标为________和________。
的两个焦点的坐标为________和________。
6.某城市1990年底人口为500万,人均住房面积为6平方米,若该城市每年人口的平均增长率为1%,为使2000年底人均住房面积达到
7.已知函数![]() 满足
满足![]() ,若
,若![]() 时,
时,![]() ,则
,则![]() 与
与![]() 的图象交点的个数是__________。
的图象交点的个数是__________。
8.若定义运算![]() 为:
为:![]() ,则函数
,则函数![]() 的值域为___________。
的值域为___________。
9.《数学手册》中有这样的结论:![]() ,其中
,其中![]() 为常数。在一个正
为常数。在一个正![]() 边形中,若它的中心到顶点的距离为
边形中,若它的中心到顶点的距离为![]() ,以
,以![]() 记此正多边形的面积,则
记此正多边形的面积,则![]() __________。
__________。
10.若以连续掷两次骰子得到的点数![]() 分别作为点
分别作为点![]() 的横坐标与纵坐标,则点
的横坐标与纵坐标,则点![]() 落在点集
落在点集![]() 且
且![]() 内的概率为____________。
内的概率为____________。
11.若不等式![]() 在
在![]() 上恒成立,则实数
上恒成立,则实数![]() 的取值范围是___________。
的取值范围是___________。
12.对于定义在![]() 上的函数
上的函数![]() ,若同时满足:①
,若同时满足:①![]() 在
在![]() 内单调;②存在区间
内单调;②存在区间![]() , 使
, 使![]() 在区间
在区间![]() 上值域为
上值域为![]() ,则函数
,则函数![]() 称为闭函数。按照上述定义,
若函数
称为闭函数。按照上述定义,
若函数![]() 为闭函数,则符合条件②的区间
为闭函数,则符合条件②的区间![]() 可以是____________。
可以是____________。
二、选择题(满分16分,每小题4分)
13.给出下列正方体的侧面展开图,其中![]() 分别是正方体的棱的中点,那么,在原正方体中,
分别是正方体的棱的中点,那么,在原正方体中,![]() 与
与![]() 所在直线为异面直线的是
( )
所在直线为异面直线的是
( )
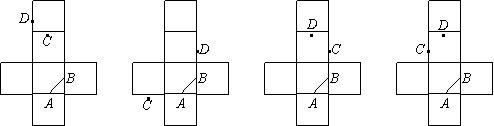 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
14.设直线![]() 关于原点对称的直线为
关于原点对称的直线为![]() ,若
,若![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() ,
,
点![]() 为椭圆上的动点,则使
为椭圆上的动点,则使![]() 的面积为
的面积为![]() 的点
的点![]() 的个数为
( )
的个数为
( )
(A)1 (B)2 (C)3 (D)4
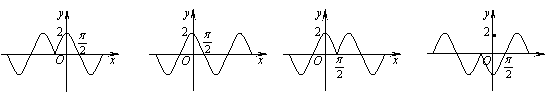 15.如图,函数
15.如图,函数![]() 的图象是
( )
的图象是
( )
(A) (B) (C) (D)
16.设![]() 是从
是从![]() 这三个整数中取值的数列,若
这三个整数中取值的数列,若![]() ,且
,且
![]() ,则
,则![]() 当中取零的个数为 ( )
当中取零的个数为 ( )
(A)10 (B)11 (C)15 (D)25
三、解答题(满分86分)
17.(本题满分12分)已知![]() ,且
,且![]() ,复数
,复数![]() ,当
,当![]() 为何值时,
为何值时,![]() 取得最大值,并求出该最大值。
取得最大值,并求出该最大值。
18.(本题满分12分)设函数![]() ,条件
,条件![]() ,条件
,条件![]() ,若
,若![]() 是
是![]() 的充分条件,求实数
的充分条件,求实数![]() 的取值范围。
的取值范围。
19.(本题满分14分,第(1)题6分,第(2)题8分)
如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,
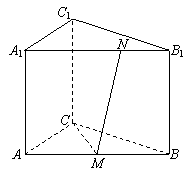
![]() 为
为![]() 上的点,且
上的点,且![]() 。
。
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小。
所成角的大小。
20.(本题满分14分,第(1)题5分,第(2)题9分)
自然状态下的鱼类是一种可再生的资源。为持续利用这一资源,需从宏观上考察其再生能力
及捕捞强度对鱼群总量的影响。用![]() 表示某鱼群在第
表示某鱼群在第![]() 年年初的总量,且
年年初的总量,且![]() 。不考虑其他因素,设在第
。不考虑其他因素,设在第![]() 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与![]() 成正比,死亡量与
成正比,死亡量与![]() 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数![]() 。
。
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)若![]() ,且
,且![]() ,试求
,试求![]() 的值,使得当且仅当从第三年起,每年年
的值,使得当且仅当从第三年起,每年年
初鱼群的总量保持不变。
21.(本题满分16分,第(1)题6分,第(2)题6分,第(3)题4分)
已知抛物线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点。
两点。
(1)求证:命题“若直线![]() 过点
过点![]() ,则
,则![]() (
(![]() 为坐标原点)”是真命题;
为坐标原点)”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由;
(3)将点![]() 向右或向左移动为点
向右或向左移动为点![]() ,直线
,直线![]() 过点
过点![]() 交
交![]() 于
于![]() 两点。当
两点。当![]() 及
及
![]() 时,分别猜测
时,分别猜测![]() 大小的变化情况(只须写出结论,不必证明)。
大小的变化情况(只须写出结论,不必证明)。
22.(本题满分18分,第(1)题4分,第(2)题6分,第(3)题8分)
已知![]() 及
及![]() 。
。
(1)求![]() 的定义域及
的定义域及![]() 的值;
的值;
(2)求![]() 的最小值;
的最小值;
(3)若![]() ,是否存在满足下列条件的正数
,是否存在满足下列条件的正数![]() ,使得对于任意的正
,使得对于任意的正
数![]() ,
,![]() 都可以成为某个三角形三边的长?若存在,则求出
都可以成为某个三角形三边的长?若存在,则求出![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
进才中学2007届高三理科月考六数学试题
一、填空题(满分48分,每小题4分)
1.在直角坐标系中,直线![]() 的倾斜角是
的倾斜角是![]() 。
。
2.若复数![]() ,则
,则![]() 0 。
0 。
3.在长方体![]() 中,若
中,若![]() ,则点
,则点![]() 到平面
到平面![]() 的距离为
的距离为
![]() 。
。
4.已知向量![]() ,若
,若![]() 三点共线,则
三点共线,则![]() 2 。
2 。
5.椭圆![]() 的两个焦点的坐标为
的两个焦点的坐标为![]() 和
和![]() 。
。
6.某城市1990年底人口为500万,人均住房面积为6平方米,若该城市每年人口的平均增长率
为1%,为使2000年底人均住房面积达到
米(用四舍五入法,精确到整数)。
7.已知函数![]() 满足
满足![]() ,若
,若![]() 时,
时,![]() ,则
,则![]()
与![]() 的图象交点的个数是 4 。
的图象交点的个数是 4 。
8.若定义运算![]() 为:
为:![]() ,则函数
,则函数![]() 的值域为
的值域为![]() 。
。
9.《数学手册》中有这样的结论:![]() ,其中
,其中![]() 为常数。在一个正
为常数。在一个正![]() 边形中,若它
边形中,若它
的中心到顶点的距离为![]() ,以
,以![]() 记此正多边形的面积,则
记此正多边形的面积,则![]()
![]() 。
。
10.若以连续掷两次骰子得到的点数![]() 分别作为点
分别作为点![]() 的横坐标与纵坐标,则点
的横坐标与纵坐标,则点![]() 落在点集
落在点集
![]() 且
且![]() 内的概率为
内的概率为![]() 。
。
11.若不等式![]() 在
在![]() 上恒成立,则实数
上恒成立,则实数![]() 的取值范围是
的取值范围是![]() 。
。
12.对于定义在![]() 上的函数
上的函数![]() ,若同时满足:①
,若同时满足:①![]() 在
在![]() 内单调;②存在区间
内单调;②存在区间![]() ,
,
使![]() 在区间
在区间![]() 上值域为
上值域为![]() ,则函数
,则函数![]() 称为闭函数。按照上述定义,
称为闭函数。按照上述定义,
若函数![]() 为闭函数,则符合条件②的区间
为闭函数,则符合条件②的区间![]() 可以是
可以是![]() 。
。
二、选择题(满分16分,每小题4分)
13.给出下列正方体的侧面展开图,其中![]() 分别是正方体的棱的中点,那么,在原正
分别是正方体的棱的中点,那么,在原正
方体中,![]() 与
与![]() 所在直线为异面直线的是
( D )
所在直线为异面直线的是
( D )
 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
14.设直线![]() 关于原点对称的直线为
关于原点对称的直线为![]() ,若
,若![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() ,
,
点![]() 为椭圆上的动点,则使
为椭圆上的动点,则使![]() 的面积为
的面积为![]() 的点
的点![]() 的个数为
( B )
的个数为
( B )
(A)1 (B)2 (C)3 (D)4
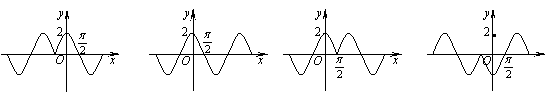 15.如图,函数
15.如图,函数![]() 的图象是
( C )
的图象是
( C )
(A) (B) (C) (D)
16.设![]() 是从
是从![]() 这三个整数中取值的数列,若
这三个整数中取值的数列,若![]() ,且
,且
![]() ,则
,则![]() 当中取零的个数为 ( B )
当中取零的个数为 ( B )
(A)10 (B)11 (C)15 (D)25
三、解答题(满分86分)
17.(本题满分12分)
已知![]() ,且
,且![]() ,复数
,复数![]() ,当
,当![]() 为何值时,
为何值时,![]() 取得最大值,并求出该最大值。
取得最大值,并求出该最大值。
17.设![]() ,且
,且![]() 。……………………………………………………………………(3分)
。……………………………………………………………………(3分)
![]() ,………………………………………………………………………(6分)
,………………………………………………………………………(6分)
![]() 。……………………………………………………(9分)
。……………………………………………………(9分)
∴当![]() ,即
,即![]() 时,
时,![]() 。……………………………………………………………………(12分)
。……………………………………………………………………(12分)
或设![]() ,
,![]() ,………………………………(4分)
,………………………………(4分)
![]() 。………………………………………………………………(8分)
。………………………………………………………………(8分)
∴当![]()
![]() 或
或![]() ,即
,即![]() 时,
时,![]() 。………………………………………(12分)
。………………………………………(12分)
18.(本题满分12分)
设函数![]() ,条件
,条件![]() ,条件
,条件![]() ,
,
若![]() 是
是![]() 的充分条件,求实数
的充分条件,求实数![]() 的取值范围。
的取值范围。
18.![]() 。………………………(4分)
。………………………(4分)
当![]() 时,
时,![]() ,即
,即![]() 。…………………………………(8分)
。…………………………………(8分)
由![]() 。………………………………………………………………(10分)
。………………………………………………………………(10分)
∵![]() 是
是![]() 的充分条件,∴
的充分条件,∴![]() ,即
,即![]() 。………………………………………………………(12分)
。………………………………………………………(12分)
19.(本题满分14分,第(1)题6分,第(2)题8分)
如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,

![]() 为
为![]() 上的点,且
上的点,且![]() 。
。
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小。
所成角的大小。
19.(1)依题意,![]() 平面
平面![]() 。……………………………………(4分)
。……………………………………(4分)
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() 。…………………………………………………(6分)
。…………………………………………………(6分)
(2)以![]() 为原点,射线
为原点,射线![]() 分别
分别![]() 轴的正方向建立空间直角坐标系,…………………(7分)
轴的正方向建立空间直角坐标系,…………………(7分)
则![]() 。
。
∴![]() ,
,![]() 。……………………………………………………………(10分)
。……………………………………………………………(10分)
设![]() 与
与![]() 所成的角为
所成的角为![]() ,
,![]() ,
,![]() 。…………………(13分)
。…………………(13分)
故异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() 。………………………………………………(14分)
。………………………………………………(14分)
20.(本题满分14分,第(1)题5分,第(2)题9分)
自然状态下的鱼类是一种可再生的资源。为持续利用这一资源,需从宏观上考察其再生能力
及捕捞强度对鱼群总量的影响。用![]() 表示某鱼群在第
表示某鱼群在第![]() 年年初的总量,且
年年初的总量,且![]() 。不考虑其他因素,设在第
。不考虑其他因素,设在第![]() 年内鱼群的繁殖量及被捕捞量都与
年内鱼群的繁殖量及被捕捞量都与![]() 成正比,死亡量与
成正比,死亡量与![]() 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数![]() 。
。
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)若![]() ,且
,且![]() ,试求
,试求![]() 的值,使得当且仅当从第三年起,每年年
的值,使得当且仅当从第三年起,每年年
初鱼群的总量保持不变。
20.(1)从第![]() 年初到第
年初到第![]() 年初,鱼群的繁殖量为
年初,鱼群的繁殖量为![]() ,被捕捞量为
,被捕捞量为![]() ,死亡量为
,死亡量为![]() 。
。
因此![]() ,即
,即![]() 。…………………(5分)
。…………………(5分)
(2)当![]() 时,
时,![]() 。………………………………………(7分)
。………………………………………(7分)
当![]() 时,
时,![]() 。∵
。∵![]() ,∴
,∴![]() 。…………………………(9分)
。…………………………(9分)
由![]() ,解得
,解得![]() (
(![]() 不合题意,舍去)。……………………(11分)
不合题意,舍去)。……………………(11分)
由![]() ,解得
,解得![]() 。………………………………………………(13分)
。………………………………………………(13分)
答:当![]() 时,可使得当且仅当从第三年起,每年年初鱼群的总量保持不变。……………(14分)
时,可使得当且仅当从第三年起,每年年初鱼群的总量保持不变。……………(14分)
21.(本题满分16分,第(1)题6分,第(2)题6分,第(3)题4分)
已知抛物线![]() ,直线
,直线![]() 交
交![]() 于
于![]() 两点。
两点。
(1)求证:命题“若直线![]() 过点
过点![]() ,则
,则![]() (
(![]() 为坐标原点)”是真命题;
为坐标原点)”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由;
(3)将点![]() 向右或向左移动为点
向右或向左移动为点![]() ,直线
,直线![]() 过点
过点![]() 交
交![]() 于
于![]() 两点。当
两点。当![]() 及
及
![]() 时,分别猜测
时,分别猜测![]() 大小的变化情况(只须写出结论,不必证明)。
大小的变化情况(只须写出结论,不必证明)。
21.(1)设直线![]() 的方程为
的方程为![]() ,…………………………………………………………………………(1分)
,…………………………………………………………………………(1分)
将![]() 代入
代入![]() ,得
,得![]() ,即
,即![]() 。………………………(3分)
。………………………(3分)
设![]() 。∵
。∵![]() ,………………………………………(5分)
,………………………………………(5分)
∴![]() ,即
,即![]() 。…………………………………………………………………………(6分)
。…………………………………………………………………………(6分)
(2)逆命题:若![]() ,则若直线
,则若直线![]() 过点
过点![]() 。它是真命题。…………………………………(8分)
。它是真命题。…………………………………(8分)
证明:设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,方程为
,方程为![]() ,
,
与![]() 联立,得
联立,得![]() 。
。
设![]() ,∵
,∵![]() ,∴
,∴![]() 。
。
∵![]() ,∴
,∴![]() 。即直线
。即直线![]() 过定点
过定点![]() 。……………………………………………………(12分)
。……………………………………………………(12分)
(3)当![]() 过
过![]() 且
且![]() 时,
时,![]() 为锐角;
为锐角;
当![]() 过
过![]() 且
且![]() 时,
时,![]() 为锐角。……………………………………………………(16分)
为锐角。……………………………………………………(16分)
22.(本题满分18分,第(1)题4分,第(2)题6分,第(3)题8分)
已知![]() 及
及![]() 。
。
(1)求![]() 的定义域及
的定义域及![]() 的值;
的值;
(2)求![]() 的最小值;
的最小值;
(3)若![]() ,是否存在满足下列条件的正数
,是否存在满足下列条件的正数![]() ,使得对于任意的正
,使得对于任意的正
数![]() ,
,![]() 都可以成为某个三角形三边的长?若存在,则求出
都可以成为某个三角形三边的长?若存在,则求出![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
22.(1)![]() 的定义域均为
的定义域均为![]() ;……………………………………………………………………(2分)
;……………………………………………………………………(2分)
![]() 。……………………………………………………………(4分)
。……………………………………………………………(4分)
(2)∵![]() ,∴
,∴![]() 。……………………………………………………(7分)
。……………………………………………………(7分)
易知函数![]() 与
与![]() 在
在![]() 上均为增函数,∴
上均为增函数,∴![]() 。(10分)
。(10分)
(3)∵![]() ,…………………………………………………………………………(11分)
,…………………………………………………………………………(11分)
∴若能构成三角形,只需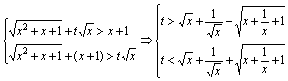 恒成立。……(13分)
恒成立。……(13分)
由(1)知,![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() 。…………………………………………(15分)
。…………………………………………(15分)
由(2)知,![]() ,∴
,∴![]() 。…………………………………………………………(17分)
。…………………………………………………………(17分)
综上,存在![]() ,满足题设条件。……………………………………………………(18分)
,满足题设条件。……………………………………………………(18分)