康杰中学河东校区
2006-2007年高三第一学期期末数学试题
一．选择题：(本大题共12小题，每小题5分，共60 分。在每小题所给出的四个选项中，只有一项是符合题目要求的)
1.已知集合
，则
等于（ ）
A.
B.
C. 
D.
2．某地区第一天下雨的概率是0.7，第二天下雨的概率是0.3，那么这两天该地区可能下雨的概率是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
3. 若曲线
的一条切线与直线
垂直,则此切线方程为（ ）
A. 
Ｂ.
Ｃ.
Ｄ. 
4.将函数
的图象按向量
平移,平移后的图象如图所示,则
平移后的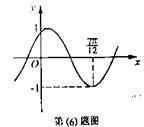
图象所对应的函数解析式是（
）
Ａ．
Ｂ．
Ｃ．
Ｄ．
5. 若互不相等的实数
成等差数列, 
成等比数列,且
（ ）
A．4 Ｂ．2 Ｃ．-2 Ｄ．-4
6.已知函数
在[-2，2]上有最大值2，则此函数在
[-2，2]上最小值为 （ ）
A．-38 Ｂ．-30 Ｃ．-6 Ｄ．-12
7. 若双曲线x2-y2=1的右支上一点P(m,n)到直线y=x的距离为
,
则m+n的值为( )
A –1/2 B 1/2 C ±1/2 D ±2
8．函数
在区间[1,2]上存在反函数的充要条件是（ ）
A．
B．
C．
D．
9．定义在R上的函数f(x)满足f(x)=f(x+2)，当
时，
，则
的大小关系是（ ）
A.
B.
C.
D．
10．对a,b
R，记max{a,b}=
，函数
的最小值是（ ）
A．0
B．
C．
D．
11.已知椭圆的离心率为e，两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e｜PF2｜=｜PF1｜,则e的值为( )
A.
B.
C.
D.以上均不对
12．设函数
给出下列四个命题：
①
时，
是奇函数
②
时，方程
只有一个实根
③的图象关于
对称
④方程至多两个实根．
其中正确的命题是( )
A．①、④ B．①、③ C．①、②、③ D．①、②、④
二、填空题（每小题4分，共16分）
13、圆（x+1）2+（y+2）2=R2，（R>0）上到直线x+y+1=0的距离为1的点恰有两个，则R的取值范围是 。
14、已知：y=f(x)与y=g(x)互为反函数，α是方程f(x)+x=10的一个根，β是方程g(x)+x=10的一个根，若f(x)=2x,则α+β的值等于 。
15．设函数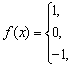
,若
，
的反函数
，则
的值为
．
16．已知
，抛物线
与x轴有两个不同交点，且两交点到原点的距离均小于1，则
的最小值为
．
三. 解答题：本大题共6小题，共74分。解答应写出文字说明，证明过程或演算步骤。
17. （本小题满分12分）
(理科) 在△ABC中，a、b、c分别是角A、B、C的对边，且
。
（I）求角B的大小；
（II）若
，求△ABC的面积。
（文科）已知△ABC中，角A、B、C对应的边为a、b、c，A=2B，
。
（1）求sinC的值；（2）若角A的内角平分线AD的长为2，求b的值。
18. （本小题满分12分）
已知二次函数f(x)=ax2+bx+c 且满足f(-1)=0对于任意实数x都有f(x)-x≥0且当x∈(0,2),时有f(x)≤(x+1)2/4
1).求f(1)的值
2).证明:a>0,c>0
3),当x∈[-1,1]时,函数 g(x)=f(x)-mx 是单调的.求m的范围
19. （本小题满分12分）
对某种赌博游戏调查后，发现其规则如下：摊主在口袋中装入8枚黑和8枚白的围棋子，参加者从中随意一次摸出5枚，摸一次交手续费1元，而中彩情况如下：
现在我们试计算如下问题：
（1）求一次获得20元彩金的概率；（结果用最简分数表示）
（2）分别求一次获2元和纪念奖的概率；（结果用最简分数表示）
（ 理科）（3）如果有1000次摸奖，摊主赔钱还是挣钱？是多少元？（精确到元）
20．（本小题满分12分）
（ 理科）函数
在区间（0，+∞）内可导，导函数
是减函数，且
设
是曲线在点（
）得的切线方程，并设函数
（Ⅰ）用
、
、
表示m；
（Ⅱ）证明：当
；
（Ⅲ）若关于
的不等式
上恒成立，其中a、b为实数，求b的取值范围及a与b所满足的关系.
（文科）已知数列
为等差数列，且
（Ⅰ）求数列
的通项公式；
（Ⅱ）证明
21.(本小题满分12分)
（ 理科）已知函数
．
（1）若函数f（x）在其定义域内为单调函数，求a的取值范围；
（2）
若函数f（x）的图象在x = 1处的切线的斜率为0，且
，已知a1 = 4，求证：an ³ 2n + 2；
（3）在（2）的条件下，试比较
与
的大小，并说明你的理由．
（文科）已知
是定义在R上的函数,其图象与x轴上的一个交点为（2，0），若
在[－1，0]和[4，5]上是减函数，在[0，2]上是增函数.
（Ⅰ）求c的值；
（Ⅱ）求d的取值范围；
（Ⅲ）在函数的图象上是否存在一点M（
），使得曲线在点M处的切线的斜率为3？若存在，求出点M的坐标；若不存在，说明理由.
22. （本小题满分14分）
（ 理科）
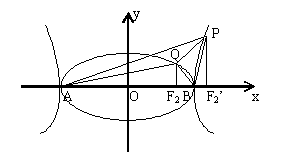
已知A、B为椭圆
和双曲线
的公共顶点，P、Q分别为双曲线和椭圆上不同于A、B的动点，且有
，设AP、BP、AQ、BQ的斜率分别为
。
（1）求证：
；
（2）设
分别为双曲线和椭圆的一个焦点（均为两曲线的右焦点），若
，求
的值。
(文科）
直线y＝x＋1与双曲线
恒有公共点。
（I）求双曲线C的离心率e的取值范围；
（II）若直线l：y＝x＋m（
）过双曲线C的右焦点F，与双曲线交于P、Q两点，并且满足
，求双曲线C的方程。
康杰中学河东校区
2006-2007年高三第一学期期末数学试题答案
1----12 。.BBACD A B DBC DC
13,(-1, +1)
14, 10。 15,4 。 16, 10。
17. （I）(理科)解法一：
由正弦定理
得
将上式代入已知
即
∵
∵
∵B为三角形的内角，∴
解法二：
由余弦定理得：
将上式代入
整理得
∴
∵B为三角形内角，∴
（II）将
代入余弦定理
得
，
∴
∴
（文科） 解：（1）
， 
18. 解：（1）f(1)=1
（2）略
（3） 
19. 解：（1）一次摸奖中20元彩金的概率
，可见可能性很小
（2）一次中2元彩金的概率 
；
（3）摊主赔钱还是挣钱由其支付完奖金余额决定，1000次收手续费1000元
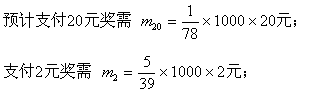
支付纪念奖需
则余额 
答：摊主应挣钱308元。
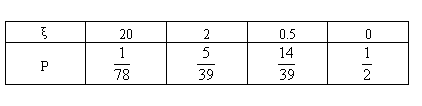
（3）另解：摸奖一次得到奖金ξ元，则随机变量ξ的分布列为：
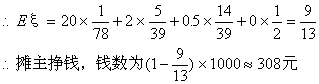
20.（ 理科）．本小题考查导数概念的几何意义，函数极值、最值的判定以及灵活运用数形结合的思想判断函数之间的大小关系.考查学生的学习能力、抽象思维能力及综合运用数学基本关系解决问题的能力.满分12分
（Ⅰ）解：
…………………………………………2分
（Ⅱ）证明：令
因为递减，所以
递增，因此，当
；
当
.所以是
唯一的极值点，且是极小值点，可知的
最小值为0，因此
即
…………………………6分
（Ⅲ）解法一：
，
是不等式成立的必要条件，以下讨论设此条件成立.
对任意
成立的充要条件是
另一方面，由于
满足前述题设中关于函数的条件，利用（II）的结果可知，
的充要条件是：过点（0，
）与曲线
相切的直线的斜率大于
，该切线的方程为
于是
的充要条件是
…………………………10分
综上，不等式
对任意成立的充要条件是
①
显然，存在a、b使①式成立的充要条件是：不等式
②
有解、解不等式②得
③
因此，③式即为b的取值范围，①式即为实数在a与b所满足的关系.…………12分
（Ⅲ）解法二：
是不等式成立的必要条件，以下讨论设此条件成立.
对任意成立的充要条件是
………………………………………………………………8分
令
，于是
对任意成立的充要条件是
由
当
时
当
时，
，所以，当
时，
取最小值.因此
成立的充要条件是
，即
………………10分
综上，不等式
对任意成立的充要条件是
①
显然，存在a、b使①式成立的充要条件是：不等式
②
有解、解不等式②得
因此，③式即为b的取值范围，①式即为实数在a与b所满足的关系.…………12分
（文科）（I）解：设等差数列
的公差为d.
由
即d=1.
所以
即
（II）证明因为
，
所以
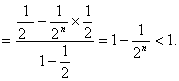
21．（本小题满分12分）（ 理科）（1）
，∴
．要使函数f（x）在定义域
内为单调函数，则在内恒大于0或恒小于0，
当
在内恒成立；
当
要使
恒成立，则
，解得
，
当
要使
恒成立，则
，解得
，
所以的取值范围为或或
．
根据题意得：
，∴
于是
，
用数学归纳法证明如下：
当
，不等式成立；
假设当
时，不等式
成立，即
也成立，
当
时，
，
所以当，不等式也成立，
综上得对所有
时5，都有
．
（3） 由（2）得
，
于是
，
所以
，
累乘得：
，
所以
（文科）解：
（Ⅰ）∵
在[－1，0]是减函数，在[0，2]上为增函数，
∴x=0点是的一个极值点.
∴
即x=0是
=0的一个根， ∴c=0.
（Ⅱ）∵
令
得：
∴
∵在[0，2]上为增函数，在[4，5]上为减函数，∴
，
即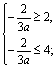
∴
∴
（Ⅲ）假设存在点M（），使得曲线在点M处的切线的斜率为3，则
即
∵
∴△=4+36a<0.
∴不存在点M（），使得曲线在点M处的切线的斜率为3
22. （ 理科）（1）证明：设点P、Q的坐标分别为
，
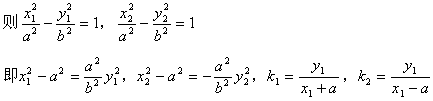
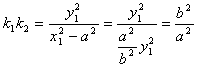
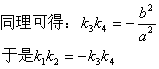
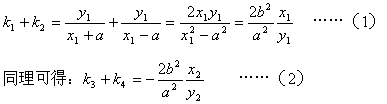
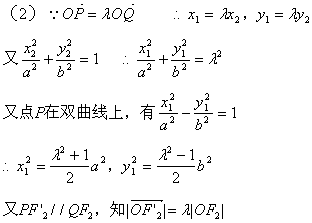
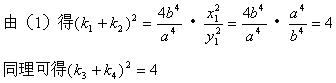
（文科） 解：（I）把y＝x＋1代入曲线
整理得
当b2＝2时，直线与双曲线有一个交点，这时
当b2≠2时，直线与双曲线恒有公共点
恒成立，即
恒成立
综上所述e的取值范围为
（II）设F（c，0），则直线l的方程为y＝x－c
把y＝x－c代入双曲线
整理得
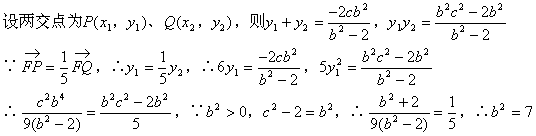
∴所求双曲线C的方程为