浙江省龙游中学2007届高三数学模拟练习卷（1）
一、选择题（本大题共10小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．已知
（ ）
A．
B．{1} C．[0，1] D．
2．已知映射
其中A=B=R，对应法则
，对于实数
.
在集合A中存在不同的两个原象，则k的取值范围是 （ ）
A．k>1 B．k≤1 C．k≥1 D．k<1
3．已知
（ ）
A．是偶函数不是奇函数 B．是奇函数不是偶函数
C．既是奇函数、又是偶函数 D．既不是奇函数又不是偶函数
4．设数列
是等差数列，且
是数列的前n项和，则 （ ）
A．
B．
C．
D．
5．若定义在区间（－1，0）内函数
满足
，则a的取值范围是
（ ）
A．（0，1） B．（1，+
） C．（0，
） D．（
）
|
则 （ ）
A．
B．
C．
D．
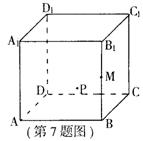
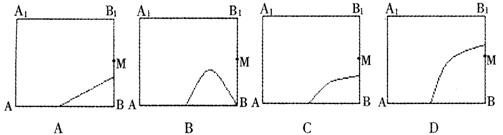
7．如图所示，在正方体ABCD—A1B1C1D1的侧面AB1内
有一动点P到平面A1C1的距离是直线BC的距离的2
倍，点M是棱BB1的中点，则动点P所在曲线的大致
| |
|
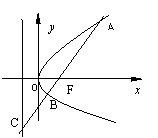8．如图，过抛物线
的焦点F的直线
交抛物线于点A、B，交其准线于点C，若
，且
，则此抛物线的方程为
( )
A．
B．
C．
D．
9．设
的图象按向量
平移后，图象恰好为函
数
的图象，则m的值可以为 （ ）
A．
B．
C．
D．
10．已知F1、F2为椭圆E的左右两个焦点，抛物线C以F1为顶点，F2为焦点，设P为椭圆与抛物线的一个交点，如果椭圆离心率为e，且
则e的值为 （ ）
A．
B．
C．
D．
二、填空题（本大题共7小题，每小题4分，共28分，把答案填在横线上。）
11．已知一平面与正方体的12条棱的夹角均为
，那么sin=
.
12．若
并且
，则实数对（m，n）表示平面上不同点的个数为___ __个
13.若函数
，的定义域R，则3a+b的取值范围是 .
14.已知点
是双曲线
上一动点,
是双曲线的两个焦点，
是坐标原点,则
取值范围是
15.设坐标平面内有一个质点从原点出发，每次沿坐标轴向正方向或负方向跳动1个单位，经过10次跳动质点落在点（2，4）处，则质点不同的运动方法共有 种（用数字作答）.
16. 已知二项式
的展开式的所有项的系数和为M，展开式的所有二项式的系数和为N，若M－N=992，则n=
17.非空集合G关于运算+满足，①对任意a、b
，都有a+b；②存在
，使对一切
都有a+e=e+a=a，则称G关于运算+的融洽集，现有下列集合和运算：
（1）G={非负整数}，+整数的加法
（2）G={偶数}，+整数的乘法
（3）G={平面向量}，+平面向量的加法
（4）G={二次三项式}，+多项式加法
其中为融洽集的为 （写出所有符合题意的序号）
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）
18．（本小题满分14分）17．（本小题满分12分）
在△ABC中，角A、B、C的对边分别为a、b、c，且满足（2a－c）cosB=bcosC.
（Ⅰ）求角B的大小；
| |
的最大值是5，求k的值.
19．（本小题满分14分）把圆周分成四等份，A是其中一个分点，动点P在四个分点上按逆时针方向前进，现投掷一个质地均匀的正四面体，它的四个面上分别写着1、2、3、4四个数字，P从A点出发，按照正四面体底面上的数字前进几个分点，转一周之前继续投掷。
Ⅰ．求点P恰好返回A点的概率.（文科只做第一问）
Ⅱ．（理做）在点P转一周恰能返回的所有结果中，用随机变量
表示点
P返回A点时的投掷次数，求的分布列和期望.
20．（本小题满分14分）
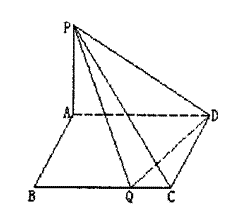如图，已知矩形ABCD中，AB=1，BC=a（a>0）,PA⊥平面—ABCD.
|
Ⅰ．问BC边上是否存在点Q，使得PQ⊥QD，并说明理由
Ⅱ．若PA=1，且BC边上有且只有一个点Q，使得
PQ⊥QD，求这时二面角Q—PD—A的大小.
21．（本小题满分14分）已知在平面直角坐标系xoy中，向量
，且
，已知P点在第一象限内.
（Ⅰ）设
的取取值范围；
（Ⅱ）设以原点O为中心，对称轴在坐标轴上，以F为右焦点的椭圆经过点M，且
取最小值时，求椭圆方程.
22．（本小题满分16分）
（理）已知
、点B1、B2……Bn……依次在射线
上，且B1（3，3）
（1）用n表示
的坐标；
（2）设直线
斜率为K，求
的值；
（3）若四边形AnAn+1Bn+1Bn面积为S，求S的取值范围.
参 考 答 案
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | D | B | A | D | C | C | D | D | C |
二、填空题：
11． 12．60 13. 
14. 
15. 9450 16.
5 17. （1）（3）
三、解答题：
18．解：（I）∵(2a－c)cosB=bcosC，
∴（2sinA－sinC）cosB=sinBcosC.……………………………………………2分
即2sinAcosB=sinBcosC+sinCcosB
=sin(B+C)
∵A+B+C=π，∴2sinAcosB=sinA.…………………………………………4分
∵0<A<π,∴sinA≠0.
∴cosB=
.…………………………………………………………………5分
∵0<B<π，∴B=
.…………………………………………………………6分
（II）
=4ksinA+cos2A.…………………………………………………………7分
=－2sin2A+4ksinA+1，A∈（0，
）……………………………………9分
设sinA=t，则t∈
.
则=－2t2+4kt+1=－2(t－k)2+1+2k2,t∈.…………………………10分
∵k>1，∴t=1时，取最大值.
依题意得，－2+4k+1=5，∴k=
.………………………………………………12分
19．解：（Ⅰ）记点P恰好返回A点为事件A1，记投掷1次、2次、3次、4次返返回A点分别为事件B1、B2、B3、B4
投掷1次返回时，；所得数为4，故
…………………………2分
投掷2次返回时，分为分别投出1，3；2，2；3，1三种情况，
故
………………………………4分
投掷3次返回时，分为分别投出1，1，2；1，2，1；2，1，1三种情况，
故
……………………6分
投掷4次返回时，分别投出1，1，1，1故
……8分
……………9分
（Ⅱ）在恰能返回A点的情况下，
………………10分
故的分布列为 1 2 3 4
P 
……………………12分
20．解：（Ⅰ）由三垂线定理得
故当
时，BC边上有两个眯，即以AD为直径的圆与BC有两个交点满足
；当
，BC边上存在一个点Q满足
时，BC边上不存在点Q满足。……6分
（Ⅱ）O此时BC=2，Q为BC中点，设G为AD中点，作
于H连QH、GQ，由题意得出
是二面角的平面角，在
中，
，
故
所求二面角大小为
……………………12分
21．解：（Ⅰ）由
得
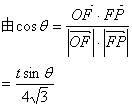
得
又
故夹角的取值范围为
…………………………4分
（Ⅱ）设
则
由（Ⅰ）知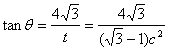
又
，
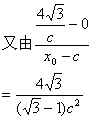得
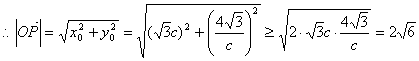……8分
当且仅当
即c=2时，
，
此时
、
故所求椭圆方程为
…………………………13分
22．（理）解：设
则由
得
①
②
①+②+……+
得
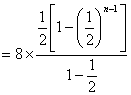
坐标为
……………………4分
设
、
则
坐标为
……………………………………6分
（2）
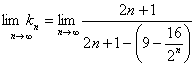
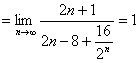………………8分
（3）
…………………………10分
记
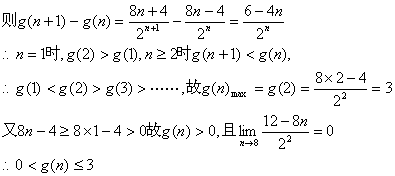……………12分
则S的取值范围为（9，12）………………13分
（文）解：（Ⅰ）令
得
即
由①可知
时，
时，
时，
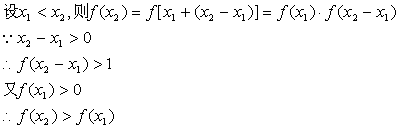
……………………………………………………4分
（Ⅱ）
由（Ⅰ）得
即的通项公式为
……………………………………8分
（Ⅲ）令
|
|
