上海市南汇区2007年4月高三数学模拟考试数学试卷
| 题号 | 一 | 二 | 三 | 总 分 | |||||
| 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 得分 | |||||||||
一．填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．
1．函数
的反函数是_______。
2．
．
3．已知等差数列
中，
=_____．
4．若非空数集A = {x｜2a —1≤x≤a+5 }，B = {x｜4≤x≤12 }，则能使
成立的所有a的集合是__________．
5．计算
.
6．抛物线
上点P的纵坐标为
，则P点到焦点F的距离为____。
7．（文）已知实数
满足不等式组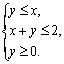
那么目标函数
的最大值是
.
（理）曲线
为参数）,如果曲线C与直线
有公共点，那么实数a的取值范围是
.
8．从五行五列数阵中（各数互不相同）任选3个数，所选的3个数既不同行又不同列的概率为_______。
9．将函数
,则
的值域是_______．
10．（文）已知某工程由下列工序组成，则工程总时数为______天．
| 工 序 | a | b | c | d | e | f | g |
| 紧前工序 | — | a | b | b | b | c,d | e,f |
| 工时数（天） | 1 | 1 | 5 | 3 | 2 | 2 | 4 |
（理）设
，那么
。
11．已知双曲线
的焦点为
、
，点
在双曲线上且
轴，则到直线
的距离为________。
12．对于各数互不相等的整数数组
(n是不小于2的正整数)，如果在
时有
，则称与是该数组的一个“逆序”，一个数组中所有“逆序”的个数称为该数组的“逆序数”。例如，数组(2,4,3,1)中有逆序“2,1”，“4,3”，“4,1”，“3,1”，其“逆序数”等于4。若各数互不相等的正整数数组
的“逆序数”是2，则
的“逆序数”是__________.
二．选择题（本大题满分16分）本大题共有4题，把正确的代号写在题后的括号内，
13．设A、B是锐角三角形ABC的两个内角，则有（ ）
A.
B.
C.
D.
14．
、
为平面M外的两条直线，如果
平面M，那么
是
平面M的（ ）
A．充分必要条件 B．必要非充分条件
C．充分非必要条件 D．既非充分又非必要条件
15．某地每年消耗木材约20万
，每价480元，为了减少木材消耗，决定按
征收木材税，这样每年的木材消耗量减少
万，为了既减少木材消耗又保证税金收入每年不少于180万元，则
的范围是（ ）
A.[1，3] B.[2，4] C.[3，5] D.[4，6]
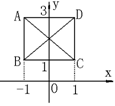16．函数y=x2－2x在区间[a，b]上的值域是[－1,3],则点（a，b）
的轨迹是图中的（ ）
A．线段AB和线段AD B．线段AB和线段CD
C．线段AD和线段BC D．线段AC和线段BD
三. 解答题（本大题满分86分）本大题共有6题，
17.（本题满分12分）已知
，
，求
的值.
18.（本题满分12分）已知
=
，
=
．（1）求函数图象的对称中心的横坐标;
（2）若
，求函数的值域．
19.（本题满分14分）已知正三棱柱ABC—A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点.⑴求正三棱柱的侧棱长.⑵求异面直线AB1与BC所成角的余弦值．
20.（本题满分14分）某货运公司今年初用98万元购进一批货车，这批货车第一年需各种费用12万元，从第二年开始，包括维修费在内，每年所需费用均比上一年增加4万元，该批货车每年运货总收入为50万元：
（I）设该批货车运货
年后开始盈利（即总收入大于买车和其它所有费用之和），求
；
(II)（理）该批货车运货若干年后，处理方案有两种：
① 到年平均盈利达到最大值时，以26万元的价格全部卖出；
② 当盈利总额达到最大值时，以8万元的价格全部卖出
问哪一种方案较合算？请说明理由。
（II）（文）几年后年平均盈利达到最大值，并求出最大值。
21.（本题满分16分）已知向量
,向量
与向量
夹角为
，且
.
（1）求向量；
（2）若向量与向量
的夹角为
，其中
，
为
的内角，且，
，依次成等差数列，试求求
的取值范围.
22.（本题满分18分）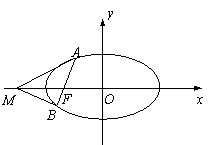 
如图，过椭圆
的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．
(1)求椭圆
的“左特征点”M的坐标；
(2)试根据(1)提出一个问题并给出解答。
2007年4月高三数学模拟试卷答案
一．1．
；2．
；3．15 ；4． 
；
5． 
；6． 
；7．（文）4；（理）
；8．
；9．
；
10．（文）13；（理）8；11．
；12． 13。
二．13．A；14．C；15． C；16． A．
三. 17.
解：显然
，故将条件等式两边同除以
，得
----------------------------------------------------------4分
解得
或
（舍去）.-------------------------------------8分
∴
------------------10分
-------12分
18. 解：(1)
--------------2分
=
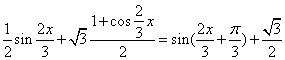-----------6分
令
中心的横坐标:
-----------------------8分
(2)由
，则
所以值域:
---------------12分
19.
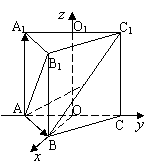解：建立如图所示的空间直角坐标系.
⑴设正三棱柱的高为h，由AB=2及正三棱柱的性质知
---------------4分
又
，
即
，则正三棱柱的侧棱长为
. ---------------7分
⑵
，---------------10分
而
∴异面直线AB1与BC所成角的余弦值为
．---------------14分
20. 解：(1)
---------------4分
(2)(理)盈利函数
对方案2：当
------------8分
对方案1：年均盈利
---------------12分
此时盈利84万元 
---------------14分
(3).(文)
---------------14分
21.解：(1)设
，有
.--------------------------------------2分
因为向量与向量夹角为，
又∵
，
，
∴
-------------------------------------------------------------------4分
解得
∴即
或
------------------------6分
(2)由
垂直知
.由2B=A+C知
----8分
若
，则
∴
----------------------------------------------------------10分
∵
,
∴
.
.
即
. ∴
-----------------------------16分
22.解：(1)解：设M(m，0)为椭圆的左特征点，
椭圆的左焦点为
，
设直线AB的方程为
将它代入得：
，
即
---------------------------------2分
设A(x1，y1)，B(x2，y2)，则
，
-----------------4分
∵∠AMB被x轴平分，∴
即
，Þ 
Þ 
∴
， ----------------------------------------6分
于是
∵
，∴
，即
∴M(
，0) ---------------------------------8分
(2) 问题不唯一，只要能在（1）基础上提出新的问题，并把所提问题解答出来就相应得分。如可以变换椭圆的方程，求出相应的M点坐标；或你想设问等。
如问题：椭圆
的“左特征点”M是一个怎样的点？
求解出M
---------------------------------18分