高三数学模拟试卷

江苏省高邮市第二中学高三数学模拟试卷2007-4-20

一、选择题(本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的)

1、已知为实数，集合，，表示把中的元素映射到集合中仍为，则等于　　　　　　　　　　　　　　　　  （　　 ）

　　 A. 　　　　 B. 　　　　　 C. 　　　　　D.

2、设函数为　　　　　　　　　　　　　　 （　　）

　　A．周期函数，最小正周期为　　　　 B．周期函数，最小正周期为

　　C．周期函数，数小正周期为　　　　D．非周期函数

3、矩形ABCD中，AB=4，BC=3，沿AC将矩形ABCD折成一个直二面角B－AC－D，则四面体ABCD的外接球的体积为 　　　　　　　　　（　　 ）

　　A．　　　　 B．　　　　 C．　　　　 D．

4、函数f (x)在定义域R内可导，若，且当时，，设，则　　　 （  ）

A．a < b < c　　　　　　 B．c < a < b 　　　　　 C．c < b < a 　　　　　 D．b < c < a

5、设是函数的反函数，则使成立的的取值范围为 (　 　 )

A、　　　　 B、　 　　　C、　　　　D、

6、已知双曲线－＝1（a＞0，b＞0）的右焦点为F，右准线与一条渐近线交于点A，△OAF的面积为（O为原点），则两条渐近线的夹角为　　　　　　　　 （　 　）

　　A．30º　　　　　　B．45º　　　　　　C．60º　　　　　　D．90º

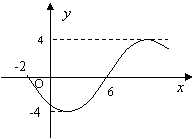
7、函数(＞0,＜ ，∈R)的部　　　　分图象如图所示，则函数表达式为　　　　（　　 ）

A．　　 B．

C．　 　　D．

8、已知抛物线的方程为y²=2px (p>0), 且抛物线上各点与焦点距离的最小值为2, 若点M在此抛物线上运动, 点N与点M关于点A(1, 1)对称, 则点N的轨迹方程为 (　　　 )

A. x²=8y　　　　　B. (x-2)²=8(y-2)　　 C. (y-2)²=-8(x-2) 　　　D. (y-2)²=8(x-2)　　

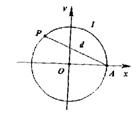
9．如图，设点A是单位圆上的一定点，动点P从点A出发在圆上按逆时针方向旋转一周，点P所旋转过的弧AP的长为l，弦AP的长为d，则函数d=f(l)的图象大致是( )

A　　　　　　　　　 B　　　　　　　　 C　　　　　　 D　

10、设函数的定义如下表,数列满足,对任意自然数均有,则的值为 ( 　 )　

	1	2	3	4	5
	4	1	3	5	2

（A）1　　　　（B）2　　　　（C）4　　　　（D）5

二、填空题：本大题共6小题，每小题5分，共30分. 把答案填在题中横线上.

11、已知数列，，把数列的各项排成三角形状，如图所示．记表示第m行，第n列的项，则=　　　　　　　　

12、 已知抛物线y²=4x,过点P(4,0)的直线与抛物线相交于A(x₁，y₁),B(x₂，y₂)两点，则的最小值是　　　.

13、已知△ABC的三个内角A、B、C成等差数列，且AB＝1，BC＝4，则边BC上的中线AD的长为　　　　　　　  ．

14、在算式：“4×□+1×□=30”的两个□中，分别填入两个自然数，使他们的倒数之和最小，则这两个数应分别为　　　 。

15、一个质点从数轴上原点出发，每次沿数轴向正方向或负方向跳动1个单位，经过10次跳动，质点与原点距离为4，则质点不同的运动方法共有　　　种（用数字作答）.

16、6个不同大小的数如图形式随机排列，　　　　　　 ▲ -------------第1行

设第一行的数为，第二、三行中的最大　　　　　 ▲　 ▲ ---------第2行

数分别为，则满足的　　　　▲　 ▲　 ▲--------第3行

概率是　　　　　

三、解答题：本大题共5小题，共70分。解答应写出文字说明、证明过程或演算步骤。

17、（本小题共12分）在ΔABC中，角A、B、C所对的边分别为a、b、c，且。

　　 （Ⅰ）求的值；（Ⅱ）若，求bc的最大值。

18、（本小题共14分）定义在上的函数，时，，且时，．

（1）证明是周期函数；

（2）求时的函数解析式；

（3）当时，最小值为，求的值．

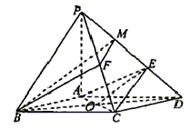
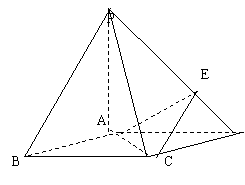
19、（本小题共14分）如图，在底面是菱形的四棱锥P—ABCＤ中，∠ABC=60⁰，PA=AC=a，PB=PD=,点E在PD上，且PE:ED=2:1.

（I）证明PA⊥平面ABCD；

（II）求以AC为棱，EAC与DAC为面的二面角的大小；

（Ⅲ）在棱PC上是否存在一点F，使BF//平面AEC？证明你的结论.

			D

20、（本小题满分14分）过抛物线上不同两点A、B分别作抛物线的切线相交于P点，（1）求点P的轨迹方程；（2）已知点F（0，1），是否存在实数使得？若存在，求出的值，若不存在，请说明理由。

21、（本小题满分16分）设=(a>0)为奇函数，且

_min=，数列{a_n}与{b_n}满足 如下关系：a₁=2，

　，． (1)求f(x)的解析表达式；

(2) 证明：当n∈N₊时， 有b_n．

参考答案

1、C；2、B3、C；4、B；5、A；6、D；7、B；8、C；9、C；10、C

11、；12、32；13、；14、5，10 ；15、240；16、.

17、解: (Ⅰ)

　　=

　　　　=

　　　=

　　　　=

(Ⅱ) ∵

∴,

又∵

∴

当且仅当 b=c=时,bc=,故bc的最大值是.

18、（1）时，，，

为周期函数且周期；　　　　　　　　　　　　　　　　 

（2）当时，则，时，，

，　　　　　　　　　　　　　

时，，；

（3）时，，，

时取“＝”，　　　　　　　　　　　　　　　　　　　 

（ⅰ）如果，即时，，即，

（ⅱ）如果即时，可以证明在上是减函数，，此时（舍去）

　　　　　　　　　 

19、解：（Ⅰ）证明　因为底面ABCD是菱形，∠ABC=60°，

所以AB=AD=AC=a，　在△PAB中，

由PA²+AB²=2a²=PB²　 知PA⊥AB.

同理，PA⊥AD，所以PA⊥平面ABCD.

（Ⅱ）解　作EG//PA交AD于G，

由PA⊥平面ABCD.

知EG⊥平面ABCD.作GH⊥AC于H，连结EH，

则EH⊥AC，∠EHG即为二面角的平面角.

又PE : ED=2 : 1，所以

从而  　

(Ⅲ ) 当F是棱PC的中点时，BF//平面AEC，证明如下，

　取PE的中点M，连结FM，则FM//CE.　①

由　 知E是MD的中点.

连结BM、BD，设BDAC=O，则O为BD的中点.

所以　BM//OE.　②

由①、②知，平面BFM//平面AEC.

又　BF平面BFM，所以BF//平面AEC.

20、解法（一）：（1）设

由得：,

　  ----------------------------------------4分

直线PA的方程是：即　　①　

同理，直线PB的方程是：　　　　　　　  ②-------------------6分

由①②得：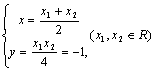

∴点P的轨迹方程是---------------------------------------------------8分

（2）由（1）得：

,

,所以

故存在=1使得--------------------------------------------------14分

解法（二）：（1）∵直线PA、PB与抛物线相切，且

∴直线PA、PB的斜率均存在且不为0，且

设PA的直线方程是

由得：----------------------------------------------4分

即

即直线PA的方程是：

同理可得直线PB的方程是：  -------------------------------------6分

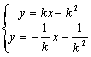由得：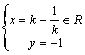

故点P的轨迹方程是-------------------------------------------------8分

（2）由（1）得：

,

故存在=1使得--------------------------------------------14分

21、解：由f(x)是奇函数，得 b=c=0，　　　　 

由f(x)_min=，得a=2，故f(x)= 　　　

(2) =，

==　　　　

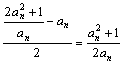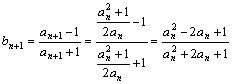∴===…=，而b₁=

∴=　　　　　　　　　　　　　　　　　　　　　 

当n=1时， b₁=，命题成立，　　　　　　　　　　　　 

当n≥2时∵2^ｎ－1＝（1＋1）^ｎ－1＝1＋≥1+=n

∴＜，即　b_n≤．