江苏省丹阳高级中学高三模拟试题一
一、选择题：（每小题5分，共50分）
1．已知
，且
，则实数a的取值范围是---------（▲）(A) 
(B) 
(C) 
(D)
2． 已知向量
，则
的值为--------------（▲）
（A）0
（B） 1
（C）
（D）2
3．直线y=x-1上的点到圆
上的点的最近距离是-----------------（▲）(A) 
(B) 
(C) 
(D) 1
4．已知一个等差数列前9项的算术平均数为10，前10项的算术平均数为11，则此等差数列的公差为--------------------------------------------------------------------------------（▲）
(A) 1
(B) 2
(C)
(D) 4
5．若
的展开式中所有奇数项的系数和为512，则展开式的中间项为----------（▲）
(A) 
(B) 
(C) 
(D) 
6．不等式
对满足a>b>c恒成立，则
的取值范围是-----------（▲）
(A) 
(B) 
(C) 
(D) 
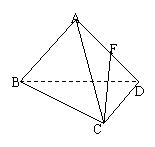
7．正三棱锥A-BCD中，F为AD
的中点，AB
CF，AB=，则
正三棱锥A-BCD的体积为----------------------（▲）
(A) (B) 
(C) 
(D) 
8．设F（x）=f（x）+f（-x），
，
是函数
的单调递增区间，将的图象按向量
平移得到一个新的函数
的图象，则的一个单调递减区间必定是-------------------------------------------------------------------------------------------（▲）(A)
(B) 
(C) 
(D)
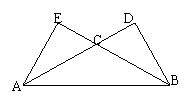9．如下图所示，在
ABC中，
，AC、BC上的高分别为BD、AE，则以A、B为
焦点，且过D、E的椭圆与双曲线的离心率的倒数
和为----------------------------------------------------（▲）
(A) 
(B) 1 (C) 
(D) 2
10．6个不同大小的数如图形式随机排列， ▲ -------------第1行
设第一行的数为
，第二、三行中的最大
▲ ▲ ---------第2行
数分别为
，则满足
的 ▲ ▲ ▲--------第3行
概率是---------------------------------------------------------------------------------------------（▲）
(A) 
(B)
(C) 
(D)
二、填空题：（每小题5分共30分）
11．有四个不同的球,四个不同的盒子,现在要把球全部放入盒内,恰有一个盒放2个球,共有 ▲ 放法；
12．已知
,则
的最大值为 ▲ ；
13．在ABC中,a,b,c是角A,B,C 的对边,(2a+c)cosB+bcosC=0,则角B= ▲ ；
14．若直线y=2a与函数
的图象有两个公共点,则a的取值范
围是 ▲ ；
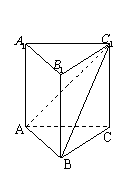
15．在正三棱柱
中,
AB=1,若
与平面
所成的
角为
,则C到平面的距离
为 ▲ ； (15题)
16．点P到点A(1,0)和直线x=-1的距离相等,且点P到直线
:y=x的距离等于
,这样的点P的个数为 ▲ 。
三、解答题：（本大题有5小题，共70分）
17．（12分）设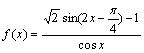
（1）求f（x）的周期和最大值；
（2）若x是第三象限角，且
，求tanx的值。
18．（14分）已知b>-1,c<0,函数f(x)=x+b的图象与函数
的图象相切
（1）求b与c的关系式；
（2）令
，且h（x）在
上有极值点，求c的范围。
19．（14分）已知椭圆C：
，经过其右焦点F且斜率为1的直线交椭圆C于A、B两点，M为AB的中点，设O为椭圆的中心，射线OM交椭圆于N点
（1）求
的值（用m表示）；
（2）证明：
。
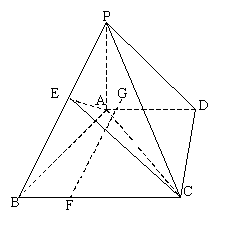
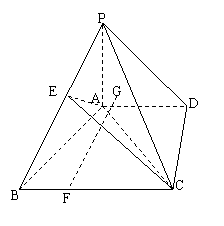
20．（14分）如图四棱锥P-ABCD中，PA平面ABCD，底面ABCD为直角梯形，
为直角，AD//BC，ABAC，AB=AC=2，G为PAC的重心，E 为PB的中点，F在线段BC上，且CF=2FB
（1）求证：FG//平面PAB；
（2）求证：FGAC；
（3）当二面角P-CD-A多大时，FG平面AEC。
 |
21．（16分）已知函数
（1）求
的反函数
；
（2）已知数列
中，
，求数列的通项公式；
（3）已知数列
中，
，求证：对一切
, 
。
江苏省丹阳高级中学高三模拟试题一参考答案
一、选择题：（每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | C | B | D | C | B | D | A | C |
二、填空题：（每小题5分共30分）
11． 144 ； 12． 2 ； 13． 1200 ；
14．
； 15． 
； 16． 3 。
三、解答题：（本大题有5小题，共70分）
17．解：⑴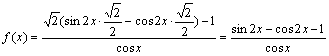
-----------2分
-----------4分
（
）
的周期
，
-----------6分
⑵由（1）得：
①，
将①两边平方得：
------8分
是第三象限角 
②--------9分
解①②得：
------------11分
-----------12分
18．解：（1）
由已知得：
----------3分
----------5分
（2）
-----------7分
令
，将
代入得：
-----------9分
若
，则
，
在R上单调递增。故不存在极值；
若
，则
有相等的两实根
，
当
时，，
在R上单调递增。故不存在极值；---------11分
若
，则有两不等的实根
，（设
），列表如下：
| x |
|
| ( |
|
|
|
| + | 0 | - | 0 | + |
|
| ↑ | ↓ | ↑ |
)
此时，x=x1和x=x2是h（x）的极值点。
∴4c2+16c+4＞0，且c＜0，解得
----------------14分
19．解：（1）F（m，0），
，和
联立得，
设A（x1，y1），B（x2，y2），则x1+x2=
，x1x2=
---------------------3分
∴
=
----7分
⑵设M（x0，y0），则
，即M（
）------------------8分
∴
----------------------------------------10分
射线OM：
代入得
∴N
12分
|
，∴----------------------------------14分
20．⑴证明：连接CG并延长交PA于H，连接BH
∵G为△PAC的重心，∴M为PA的中点且
CG：GH=2：1，又CF：FB=2：1，
∴CG：GH=CF：FB=2：1，∴FG∥BH，
易得FG//平面PAB------------------------------4分
⑵∵PA平面ABCD，∴PAAC，
∵ABAC，∴AC平面PAB，
BH
平面PAB，∴ACBH，∴FGAC---------------------------------------------------7分
⑶∵PA平面ABCD，∴CDAD，∴PDCD
∴∠PDA为二面角P-CD-A的平面角。
若FG平面AEC，则BH平面AEC，∴BHAE-------------------------------------9分
设BH交AE于O，PA=a，∵AB=2，PAAB，∴
∵E、H分别是PB、PA的中点，∴O为△PAB的重心。----------------------11分
∴
∵AO2+BO2=AB2，∴
∴
。---------------------------13分
∵AB=AC=2，ABAC，∴∠CAD=∠ACB=450，∴
，
∴
，
∴二面角P-CD-A的大小为arctan2时，FG平面AEC---------------------------------14分
21．解：(1)
----------------3分
(2)
------------5分
成等差数列,d=1 
----------7分
(3)
---------------------8分
--------------------------10分
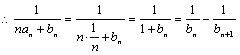----------------------------------------------------11分
----------------------------------14分
又
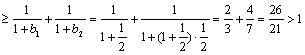--------------------------------------16分
