钦州市大寺中学2007届高三毕业班数学[理]模拟练习(1)
一.选择题(每小题5分,共60分)
1.复数![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知不等式![]() 的解集为A,函数
的解集为A,函数![]() 的定义或为B,则
的定义或为B,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.将函数![]() 的图象按向量a平移后,得到
的图象按向量a平移后,得到![]() 的图象,则
的图象,则
A.a=(1,2) B.a=(1,-2) C.a=(-1,2) D.a=(-1,-2)
4.在![]() 的展开式中
的展开式中![]() 的系数是
的系数是
A.240 B.15 C.-15 D.-240
5.若随机变量![]() 的分布列是:
的分布列是:
|
| 1 | 3 | 5 |
|
| 0.2 | 0.6 |
|
则其数学期望![]() 等于
等于
A.1 B.![]() C.
C.![]() D.3
D.3
6.某班上午要上语文、数学、英语、体育各一节,体育课既不在第一节也不在第四节,共有不同的排法数为
A.24 B.22 C.20 D.12
7.数列![]() 中,已知对任意正整数
中,已知对任意正整数![]() ,
,![]() ,则
,则![]() 等于
等于
A.(2n-1)2 B.![]() (2n-1) C.
(2n-1) C.![]() (4n-1) D.4n-1
(4n-1) D.4n-1
8.设双曲线![]() 的两条渐近线与右准线的三角形区域(包含边界)为D,P(x,y)为D内一个动点,则目标函数
的两条渐近线与右准线的三角形区域(包含边界)为D,P(x,y)为D内一个动点,则目标函数![]() 的最小值为
的最小值为
A.-2 B.![]() C.0 D.
C.0 D.![]()
9.已知函数![]() ,则f(一3)与f(2)的大小关系是
,则f(一3)与f(2)的大小关系是
A.f(一3)<f(2) B.f(一3)> f(2) C.f(一3)= f(2) D.不能确定
10.有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记3的对面的数字为m,4的对面的数字为n,那么m+n的值为
A.3 B.7 C.8 D.11
|
11.已知定义在![]() 上的函数
上的函数![]() 同时满足条件:(1)
同时满足条件:(1)![]() ;(2)
;(2)![]() ,且
,且![]() ;(3)当
;(3)当![]() 时,
时,![]() .若
.若![]() 的反函数是
的反函数是![]() ,则不等式
,则不等式![]() 的解集为
的解集为
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
12.A,B两位同学各有3张卡片,现以投掷均匀硬币的形式进行游戏,当出现下面向上时A赢得B一张卡片,否则B赢得A一张卡片。如果某人已赢得所有卡片,则游戏终止。那么恰好掷完5次硬币时游戏终止的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二.填空题(每小题4分,共16分)
13.在△ABC中,a,b,c分别为角A,B,C的对边,且满足![]() 则角A的大小是
.
则角A的大小是
.
14.设(3x-1)n=a0+a1x+a2x2+…+anxn,已知a0+a1+a2+…+an=128,则a2=
15.在等差数列![]() 中,
中,![]() 现从
现从![]() 的前10项中随机取数,每次取出一个数,取后放回,连续抽取3次,假定每次取数互不影响,那么在这三次取数中,取出的数恰好为两个正数和一个负数的概率为
(用数字作答).
的前10项中随机取数,每次取出一个数,取后放回,连续抽取3次,假定每次取数互不影响,那么在这三次取数中,取出的数恰好为两个正数和一个负数的概率为
(用数字作答).
16.定义在(-1,1)上的函数![]() ,
,![]() 的取值范围为
.
的取值范围为
.
三.解答题(第17、18、19、20、21题每题12分,第22题14分,共74分)
17.已知函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(Ⅰ)求实数![]() 的值;(Ⅱ)解关于
的值;(Ⅱ)解关于![]() 的不等式
的不等式![]() .
.
18.在△ABC中,∠A、∠B、∠C的对边的边长分别为a、b、c,且a,b,c成等比数列.
(1)求角B的取值范围;
(2)若关于角B的不等式![]() 恒成立,求m的取值范围.
恒成立,求m的取值范围.
19.如图, 正方形ABCD和ABEF的边长均为1,且它们所在的平面互相垂直,G为BC的中点.
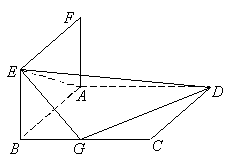 (Ⅰ)求点G到平面ADE的距离;
(Ⅰ)求点G到平面ADE的距离;
(Ⅱ)求直线AD与平面DEG所成的角;
20.已知函数![]() 的定义域是
的定义域是![]() 且当
且当![]() 时,满足
时,满足![]()
(I)判断函数![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(II)已知![]() 、
、![]() N*且
N*且![]() 证明:
证明:![]()
21.设![]() ,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
,定点F(a,0),直线l :x=-a交x轴于点H,点B是l上的动点,过点B垂直于l的直线与线段BF的垂直平分线交于点M.
(I)求点M的轨迹C的方程;
(II)设直线BF与曲线C交于P,Q两点,证明:向量![]() 、
、![]() 与
与![]() 的夹角相等.
的夹角相等.
22.已知函数![]() (x≥4)的反函数为
(x≥4)的反函数为![]() ,数列
,数列![]() 满足:a1=1,
满足:a1=1,![]() ,(
,(![]() N*),数列
N*),数列![]() ,
,![]() ,
,![]() ,…,
,…,![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列.
的等比数列.
(Ⅰ)求证:数列![]() 为等差数列;(Ⅱ)若
为等差数列;(Ⅱ)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
钦州市大寺中学2007届高三数学[理科]模拟练习(1)
参考答案
一.选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | D | A | D | D | C | B | A | C | B | D |
二.填空题
13.![]() ;14.-189;15.
;14.-189;15.![]() ;16.
;16.![]() 。
。
三.解答题
17.(Ⅰ)由条件知![]()
由![]() 得
得![]() ,即
,即![]()
![]()
![]() ┅┅┅┅┅┅┅4分
┅┅┅┅┅┅┅4分
(Ⅱ)![]()
![]() ,
,![]()
![]() ,即
,即![]() ,
,![]()
![]() (
(![]() )
┅┅┅┅┅8分
)
┅┅┅┅┅8分
①当m>-1 时
![]()
![]() 为
为![]() ,
,![]() ┅┅┅9分
┅┅┅9分
②当m=-1 时
(![]() )为
)为![]()
![]() ┅┅┅┅┅10分
┅┅┅┅┅10分
③当m<-1 时
![]() , (
, (![]() )为
)为![]() 又
又![]() ,
,
![]() ┅┅┅┅┅12分
┅┅┅┅┅12分
18.(1)![]()
当且仅当a=b=c时,![]()
![]() (5分)
(5分)
(2)![]()
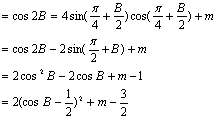
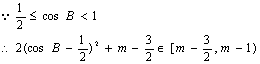
∵不等式![]() 恒成立,
恒成立,
![]() ,故m的取值范围为
,故m的取值范围为![]() (12分)
(12分)
19.(Ⅰ)∵BC∥AD, AD![]() 面ADE,
面ADE,
∴点G到平面ADE的距离即点B到平面ADE的距离.
连BF交AE于H,则BF⊥AE,又BF⊥AD.
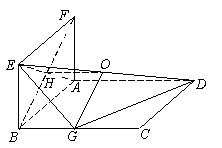 ∴BH即点B到平面ADE的距离.………………………(2分)
∴BH即点B到平面ADE的距离.………………………(2分)
在Rt△ABE中,![]() .
.
∴点G到平面ADE的距离为![]() .…(4分)
.…(4分)
(Ⅱ)设DE中点为O,连OG, OH,
则OH ![]()
![]() AD,BG
AD,BG ![]()
![]() AD.
AD.
∴四边形BHOG为平行四边形.………………………(6分)
∴GO∥BH.
由(Ⅰ)BH⊥面ADE,∴GO⊥面ADE.………………………(8分)
又GO![]() 面DEG.∴面DEG⊥面ADE.
面DEG.∴面DEG⊥面ADE.
∴过点A作AM⊥DE于M,则AM⊥面DEG.
∴![]() 为直线AD与平面DEG所成的角.………………………(10分)
为直线AD与平面DEG所成的角.………………………(10分)
在Rt△ADE中,![]() .∴
.∴![]() .
.
∴直线AD与平面DEG所成的角为![]() .………………………(12分)
.………………………(12分)
20.(1)![]() ……………………………………2分
……………………………………2分
又![]() 所以当
所以当![]() 时,
时,![]()
![]() 即
即![]() …………………………4分
…………………………4分
因此函数![]() 在
在![]() 上是单调递减函数。…………………6分
上是单调递减函数。…………………6分
(2)![]() 设
设![]() 且
且![]()
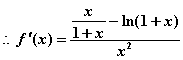 ……………………………………8分
……………………………………8分
![]()
![]()
![]() 在
在![]() 内为减函数…………………10分
内为减函数…………………10分
![]()
![]()
![]()
![]() …………………12分
…………………12分
其它参考方法:
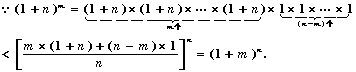
21.(I)解:连接MF,依题意有MF=MB,…………………………………………3分
所以动点M的轨迹是以F(![]() ,0)为焦点,直线l: x=-
,0)为焦点,直线l: x=-![]() 为准线的抛物线,
为准线的抛物线,
所以C的方程为![]() ………………………………………………5分
………………………………………………5分
(II)解:设P,Q的坐标分别为![]()
依题意直线BF的斜率存在且不为0,设直线BF的方程为![]()
将其与C的方程联立,消去y得
![]() ,故
,故![]() ………8分
………8分
记向量![]()
因为![]()
所以![]() ……11分
……11分
同理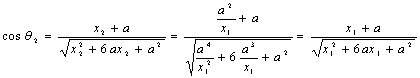
因为![]()
所以![]() 即向量
即向量![]() 、
、![]() 与
与![]() 的夹角相等。……………………14分
的夹角相等。……………………14分
22.(Ⅰ)∵![]()
![]() (x≥4),
(x≥4),
∴![]()
![]() (x≥0), ……………………………………(2分)
(x≥0), ……………………………………(2分)
∴![]()
![]() ,
,
即![]() (
(![]() N*). ……………………………(4分)
N*). ……………………………(4分)
∴数列![]() 是以
是以![]() 为首项,公差为2的等差数列.……………(6分)
为首项,公差为2的等差数列.……………(6分)
(Ⅱ)由(Ⅰ)得:![]() ,即
,即![]() (
(![]() N*).
…(8分)
N*).
…(8分)
b1=1,当n≥2时,![]() ,
,
∴![]()
![]()
![]()
因而![]() ,
,![]() N*. ……………………………(10分)
N*. ……………………………(10分)
![]()
![]() ,
,
∴![]()
![]()
![]()
令![]()
![]() ①
①
则![]()
![]() ②
②
①-②,得
![]()
![]()
![]()
∴![]() .又
.又![]() .
.
∴![]() . ……………………………(14分)
. ……………………………(14分)
