天津市蓟县高级中学2006-2007学年度高三数学理科模拟考试卷
一、 选择题(每小题5分,本题满分60分)
1.设![]()
A.[2,4] B.![]() C.[-2,4] D.
C.[-2,4] D.![]()
2.用数学归纳法证明:![]() 时,从
时,从![]() 到
到![]() 时应增添的式子是
时应增添的式子是
A.![]() B.
B.![]() C.
C.![]() C.
C.![]()
3.设函数![]()
A. 0 B.—1 C.1 D.2
4. 在半径为10的球面上有![]() 、
、![]() 、
、![]() 三点,如果
三点,如果![]() ,
,![]() ,则球心
,则球心![]() 到平面
到平面![]() 的距离为
的距离为
A.8 B.6 C.4 D.2
5. 一系列椭圆都以坐标原点为中心,以定直线![]() 为准线,且中心到准线
为准线,且中心到准线![]() 的距离为2,若这一系列椭圆的离心率组成以
的距离为2,若这一系列椭圆的离心率组成以![]() 为首项,
为首项,![]() 为公比的等比数列,而椭圆相应的长半轴长为
为公比的等比数列,而椭圆相应的长半轴长为![]() ,则
,则![]()
![]()
![]()
6.函数![]() 的反函数是
的反函数是
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
7. 已知两直线m、n,两平面α、β,且![]() .下面有四个命题:
.下面有四个命题:
1)若![]() ; 2)
; 2)![]() ;
;
3)![]() ; 4)
; 4)![]() .
.
其中正确命题的个数是:
A.3 B.1 C.4 D. 2
8. 函数![]() 的图象关于
的图象关于
A.![]() 轴对称
B.直线
轴对称
B.直线![]() 对称 C.原点对称 D.
对称 C.原点对称 D.![]() 轴对称
轴对称
9.已知在函数![]() 图像上,相邻的一个最大值点与一个最小值点恰好在
图像上,相邻的一个最大值点与一个最小值点恰好在![]() 上,则
上,则![]() 的最小正周期为
的最小正周期为
A.4 B.3 C.2 D. 1
10.若某等差数列{an}中,a2+a6+a16为一个确定的常数,则其前n项和Sn中也为确定的常数的是
A.S17 B.S15 C.S8 D.S7
11.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为
A.2 B.![]() C.4 D.
C.4 D.![]()
12.设过点![]() 的直线分别与
的直线分别与![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴交于
轴的正半轴交于![]() 、
、![]() 两点,点
两点,点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,![]() 为坐标原点,若
为坐标原点,若![]() ,且
,且![]() ,则
,则![]() 点的轨迹方程是
点的轨迹方程是
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
二、 填空题(每小题4分,本题满分16分)
13.二项式(x-![]()
14. ![]() 的三内角
的三内角![]() 所对边的长分别为
所对边的长分别为![]() 设向量
设向量![]() ,
,
![]() ,若
,若![]() ,则角
,则角![]() 的大小为________.
的大小为________.
15.若直线![]() ,
,![]() 过圆
过圆![]() 的圆心,则
的圆心,则![]() 的最小值为
.
的最小值为
.
16.某校高一、高二、高三三个年级的学生数分别为1500人、1200和1000人,现采用按年级分层抽样法了解学生的视力状况,已知在高一年级抽查了75人,则这次调查三个年级共抽查了 人.
三、 解答题(本大题共6小题,本题满分74分)
17.(本题满分12分)
已知向量![]()
(Ⅰ)求cos(![]() —
—![]() )的值
)的值
(Ⅱ)若![]() 的值
的值
18.(本题满分12分)
从4名男生和2名女生中任选3人参加演讲比赛。设随机变量![]() 表示所选3人中女生的人数。
表示所选3人中女生的人数。
(I) 求![]() 的分布列;
的分布列;
(II) 求![]() 的数学期望;
的数学期望;
(III) 求“所选3人中女生人数![]() ”的概率。
”的概率。
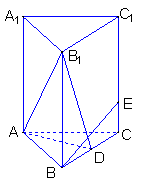 19(本题满分12)
19(本题满分12)
如图在直三棱柱ABC-![]() 中,∠BAC=90°,
中,∠BAC=90°,
AB=AC=2,![]() ,D为BC的中点,E为
,D为BC的中点,E为![]() 上的点,且CE=1
上的点,且CE=1![]()
(Ⅰ)求证![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小
的大小![]()
20![]() (本题满分12分)
(本题满分12分)
已知![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,
,![]() ,
,![]() ,
,
(Ⅰ)求![]()
![]()
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]() ,求
,求![]()
![]()
21.(本题满分14)
已知中心在原点的椭圆C的左焦点为![]() ,右顶点为(2,0).
,右顶点为(2,0).
(1)求椭圆C的方程;
(2)若直线![]() 与椭圆C有两个不同的交点A和B,且
与椭圆C有两个不同的交点A和B,且![]() (其中O为原点), 求 实数m的取值范围.
(其中O为原点), 求 实数m的取值范围.
22、(本题满分12分)
已知函数:![]()
(Ⅰ)证明:f(x)+2+f(2a-x)=0对定义域内的所有x都成立.
(Ⅱ)当f(x)的定义域为[a+![]() ,a+1]时,求证:f(x)的值域为[-3,-2];
,a+1]时,求证:f(x)的值域为[-3,-2];
(Ⅲ)设函数g(x)=x2+(x-a)f(x) ,求g(x) 的最小值 .
[参考答案]
一、选择题(每小题5分,共60分):
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | B | A | B | D | C | D | C | A | B | C | D |
二、填空题
13. -84 14. ![]() 15. 16
16. 185
15. 16
16. 185
三、解答题
17.解:(1)![]() ;
;
![]() ……………2分
……………2分
![]() ……………3分
……………3分
![]() ……………6分
……………6分
(2)![]() ………………7分
………………7分
![]()
![]() ………………9分
………………9分
![]()
![]() ………………12分
………………12分
18.解:(I)![]() 可能取的值为
可能取的值为![]() 。
。
![]()
所以,![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
| P |
|
|
|
………………8分
(II):由(I),![]() 的数学期望为
的数学期望为
![]() ………………10分
………………10分
(III):由(I),“所选3人中女生人数![]() ”的概率为
”的概率为
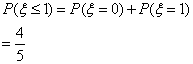 ………………12分
………………12分
19.解法一:
(Ⅰ)由![]() ,
,![]() 是
是![]() 的中点,得
的中点,得![]()
![]()
从而![]() 平面
平面![]()
又![]() 平面
平面![]() ,所以
,所以![]() .
.
由已知![]() ,
,![]() ,得
,得![]()
在![]() 中,
中,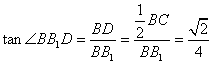
在![]() 中,
中,![]()
于是![]() ,设
,设![]()
![]() ,则
,则![]() ,又
,又![]()
故![]() 平面
平面![]() …………………5分
…………………5分
(Ⅱ)过点![]() 作
作![]() 于
于![]() ,连接
,连接![]()
由(Ⅰ)及三垂线定理可知![]() 是
是![]() 的平面角.
的平面角.
在![]() 中,由
中,由![]() ,得
,得![]()
在![]() 中,由
中,由![]() ,得
,得![]()
所以在![]() 中,
中,![]()
故二面角![]() 的大小为
的大小为![]() …………………12分
…………………12分
解法二:
(Ⅰ)如图,建立空间直角坐标系![]()
易知![]()
可得 ![]()
于是得 ![]() ,可知
,可知![]() ,
,![]()
又![]() ,故
,故![]() 平面
平面![]() …………………6分
…………………6分
(Ⅱ)由(Ⅰ)知平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]()
于是 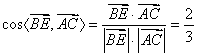
故二面角![]() 的大小为
的大小为![]() …………………12分
…………………12分
20.解:(Ⅰ)当![]() 时,
时,![]()
![]()
![]() .由
.由![]() ,得
,得![]()
当![]() 时,
时, ![]()
整理得 ![]() ,
, ![]()
由![]() ,只有
,只有 ![]() ,即
,即 ![]()
所以![]() 是
是![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,
![]() …………………6分
…………………6分
(Ⅱ) 由(Ⅰ)得![]()
![]()
所以
![]()
即 ![]() ,
,
又![]() ,所以
,所以 ![]() …………………12分
…………………12分
21.解:(Ⅰ)设椭圆方程为![]()
![]()
由已知得![]()
故椭圆C的方程为![]() ………………………4分
………………………4分
(Ⅱ)将![]()
![]()
由直线l与椭圆C交于不同的两点得![]()
即![]() ①
………………8分
①
………………8分
设![]() ,则
,则
![]() …………………10分
…………………10分
![]()
而![]()
![]()
于是![]() 即
即![]() ② ………………………12分
② ………………………12分
由①、②得 ![]()
故m的取值范围为![]() ………………14分
………………14分
22.(Ⅰ)证明:![]()
![]()
∴结论成立 ……………………………………2分
(Ⅱ)证明:![]()
当
![]()
![]()
![]()
即![]() …………6分
…………6分
(Ⅲ)解:![]()
(1)当![]()
如果![]() 即
即![]() 时,则函数在
时,则函数在![]() 上单调递增
上单调递增
![]()
如果![]()
当![]() 时,
时,![]() 最小值不存在 …………………9分
最小值不存在 …………………9分
(2)当![]()
如果![]()
如果![]()
![]() ………………13分
………………13分
当![]()
![]()
综合得:当![]() 时 g(x)最小值是
时 g(x)最小值是![]()
当![]() 时 g(x)最小值是
时 g(x)最小值是![]()
当![]() 时 g(x)最小值为
时 g(x)最小值为![]()
当![]() 时 g(x)最小值不存在………………12分
时 g(x)最小值不存在………………12分