2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(8)— 《立体几何》
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出下列四个命题
①垂直于同一直线的两条直线互相平行.②垂直于同一平面的两个平面互相平行.③若直线![]() 与同一平面所成的角相等,则
与同一平面所成的角相等,则![]() 互相平行.④若直线
互相平行.④若直线![]() 是异面直线,则与
是异面直线,则与![]() 都相交的两条直线是异面直线.其中假命题的个数是 ( )
都相交的两条直线是异面直线.其中假命题的个数是 ( )
A.1 B.2 C.3 D.4
2.将正方形ABCD沿对角线BD折成一个120°的二面角,点C到达点C1,这时异面直线AD与BC1所成角的余弦值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.一个长方体共一顶点的三个面的面积分别是![]() 、
、![]() 、
、![]() ,这个长方体对角线的长为( )
,这个长方体对角线的长为( )
A.2![]() B.3
B.3![]() C.6
D.
C.6
D.![]()
4.已知二面角α-l-β的大小为600,m、n为异面直线,且m⊥α,n⊥β,则m、n所成的角为
( )
|
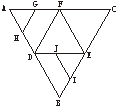
5.如图,在正三角形ABC中,D、E、F分别为各边的中点,
G、H、I、J分别为AF、AD、BE、DE的中点.将△ABC
沿DE、EF、DF折成三棱锥以后,GH与IJ所成角的度
数为 ( )
A.90° B.60°
C.45° D.0°
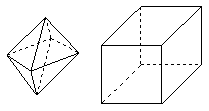 6.两相同的正四棱锥组成如图所示的几何体,可放棱长
6.两相同的正四棱锥组成如图所示的几何体,可放棱长
为1的正方体内,使正四棱锥的底面ABCD与正方
体的某一个平面平行,且各顶点均在正方体的面上,
则这样的几何体体积的可能值有 ( )
A.1个 B.2个
C.3个 D.无穷多个
7.正方体A′B′C′D′—ABCD的棱长为a,EF在AB上滑动,且EF=b(b<a=,Q点在D′C′上滑动,则四面体A′—EFQ的体积为 ( )
A.与E、F位置有关 B.与Q位置有关
C.与E、F、Q位置都有关 D.与E、F、Q位置均无关,是定值
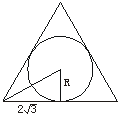
8.(理)高为5,底面边长为4![]() 的正三棱柱形容器(下有底),可放置最大球的半径是( )
的正三棱柱形容器(下有底),可放置最大球的半径是( )
A.![]() B.2
C.
B.2
C.![]() D.
D.![]()
(文)三个两两垂直的平面,它们的三条交线交于一点O,点P到三个平面的距离比为1∶
2∶3,PO=2![]() ,则P到这三个平面的距离分别是 ( )
,则P到这三个平面的距离分别是 ( )
A.1,2,3 B.2,4,6 C.1,4,6 D.3,6,9
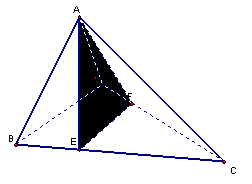 9.如图,在四面体ABCD中,截面AEF经过四
9.如图,在四面体ABCD中,截面AEF经过四
面体的内切球(与四个面都相切的球)球心O,
且与BC,DC分别截于E、F,如果截面将四
面体分成体积相等的两部分,设四棱锥A-
BEFD与三棱锥A-EFC的表面积分别是S1,
S2,则必有 ( )
A.S1<S2
B.S1>S2
C.S1=S2
D.S1,S2的大小关系不能确定
10.已知球o的半径是1,ABC三点都在球面上,AB两点和AC两点的球面距离都是![]() ,BC两点的球面距离是
,BC两点的球面距离是![]() ,则二面角B-OA-C的大小是 ( )
,则二面角B-OA-C的大小是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.条件甲:四棱锥的所有侧面都是全等三角形,条件乙:这个四棱锥是正四棱锥,则条件甲是条件乙的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
12.已知棱锥的顶点为P,P在底面上的射影为O,PO=a,现用平行于底面的平面去截这个棱锥,截面交PO于点M,并使截得的两部分侧面积相等,设OM=b,则a与b的关系是 ( )
A.b=(![]() -1)a B.b=(
-1)a B.b=(![]() +1)a
+1)a
C.b=![]() D.b=
D.b=![]()
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)
13.已知正四棱锥的体积为12,底面对角线的长为![]() ,则侧面与底面所成的二面角等于_______________.
,则侧面与底面所成的二面角等于_______________.
14.若一条直线与一个正四棱柱各个面所成的角都为![]() ,则
,则![]() =______.
=______.
 15.若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为___________.
15.若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为___________.
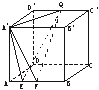
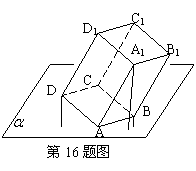
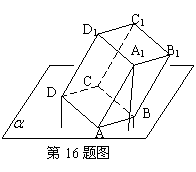
16.多面体上,位于同一条棱两端的顶点称为相邻的,
如图,正方体的一个顶点A在平面![]() 内,其余顶
内,其余顶
点在![]() 的同侧,正方体上与顶点A相邻的三个顶
的同侧,正方体上与顶点A相邻的三个顶
点到![]() 的距离分别为1,2和4,P是正方体的其
的距离分别为1,2和4,P是正方体的其
余四个顶点中的一个,则P到平面![]() 的距离可能
的距离可能
是: ( )
①3; ②4; ③5; ④6; ⑤7
以上结论正确的为______________.(写出所有正
确结论的编号)
三、解答题(本大题共6小题, 共74分,解答应写出文字说明,证明过程或演算步骤)
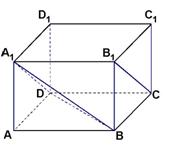
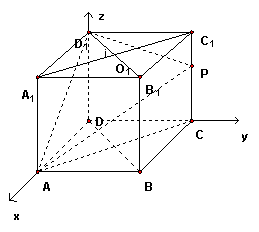
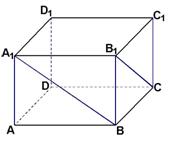 17.(本小题满分12分)在长方体
17.(本小题满分12分)在长方体![]() 中,已知
中,已知![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
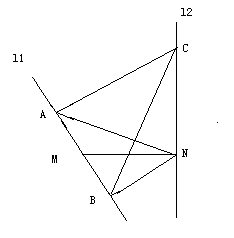
18.(本小题满分12分)如图,![]() 、
、![]() 是互相垂直的异面直线,MN是它们的公垂线段。点A、B在
是互相垂直的异面直线,MN是它们的公垂线段。点A、B在![]() 上,C在
上,C在![]() 上,
上,![]() .
.
(1)证明![]() ⊥
⊥![]() ;
;
(2)若![]() ,求
,求![]() 与平面ABC所成角的余弦值.
与平面ABC所成角的余弦值.
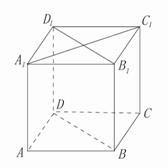
19.(本小题满分12分)如图,在棱长为1的正方体![]() 中,
中,![]() 是侧棱
是侧棱![]() 上的一点,
上的一点,![]() .
.
(1)试确定![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ;
;
 (2)在线段
(2)在线段![]() 上是否存在一个定点
上是否存在一个定点![]() ,使得对任意的
,使得对任意的![]() ,
,![]() 在平面
在平面![]() 上的射影垂直于
上的射影垂直于![]() .并证明你的结论.
.并证明你的结论.
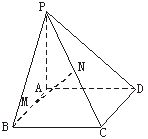
20.(本小题满分12分)(理)如图,已知矩形ABCD,PA⊥平面ABCD,M、N分别是AB、PC的中点,设AB=a,BC=b,PA=c.
(1)建立适当的空间直角坐标系,写出A、B、M、N点的坐标,并证明MN⊥AB;
(2)平面PDC和平面ABCD所成的二面角为θ,当θ为何值时(与a、b、c无关),
|
(文)正方体ABCD—A1B1C1D1中,M、N、P分别为棱AB、BC、DD1的中点.
(1)求证:PB⊥平面MNB1;
(2)设二面角M—B1N—B为α,求cosα的值.
21.(本小题满分12分)已知正方形![]() .
.![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,将ADE沿
的中点,将ADE沿![]() 折起,如图所示,记二面角
折起,如图所示,记二面角![]() 的大小为
的大小为![]() .
.
(1)证明![]() 平面
平面![]() ;
;
(2)若![]() 为正三角形,试判断点
为正三角形,试判断点![]() 在平面
在平面![]() 内的射影
内的射影![]() 是否在直线
是否在直线![]() 上,证明你的结论,并求角
上,证明你的结论,并求角![]() 的余弦值.
的余弦值.
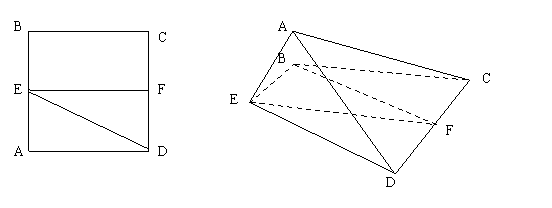

22.(本小题满分14分)如图,在长方体ABCD─A1B1C1D1中,E、P分别是BC、A1D1的中点,M、N分别是AE、CD1的中点,AD=AA1=a,AB=2a.
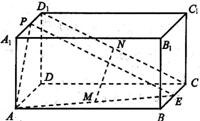 (1)求证:MN∥面ADD1A1;
(1)求证:MN∥面ADD1A1;
(2)求二面角P─AE─D的大小;
(3)求三棱锥P─DEN的体积.
参考答案(8)
1. D.利用特殊图形正方体我们不难发现①、②、③、④均不正确,故选择答案D.
2. D.由题意易知∠ABC1是AD与BC1所成的角,解△ABC1,得余弦为![]() .答案:D.
.答案:D.
3. D.设长宽高为a、b、c,则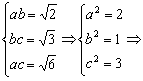 l=
l=![]() ,答案:D.
,答案:D.
4. B. 作图可知满足条件的m、n所成的角1200为故应选B.
5. B.平面图形折叠后为正三棱锥.如图,取EF的中点M,连结IM、MJ,则MJ![]()
![]() FD,GH
FD,GH![]()
![]() FD,∴MJ∥GH,∠IJM为异面直线GH与JI所成的角.
FD,∴MJ∥GH,∠IJM为异面直线GH与JI所成的角.
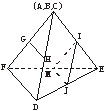
由已知条件易证△MJI为正三角形.∴∠IJM=60°.答案:B.
6. D. 法一:本题可以转化为一个正方形可以有多少个内接正方形,显然有无穷多个
|
7. D.VA′-EFQ=VQ-A′EF.
|
(文)B.
9. C .连OA、OB、OC、OD则VA-BEFD=VO-ABD+VO-ABE+VO-BEFD
VA-EFC=VO-ADC+VO-AEC+VO-EFC又VA-BEFD=VA-EFC而每个三棱锥的高都是原四面体的内切球的半径,故SABD+SABE+SBEFD=SADC+SAEC+SEFC又面AEF公共,故选C
|
11. B.乙![]() 甲,但甲
甲,但甲![]() 乙,例如四棱锥S—ABCD
乙,例如四棱锥S—ABCD
的底面ABCD为菱形,但它不是正四棱锥.
12. C.由平行锥体底面的截面性质,知![]() =
=![]() ,∴
,∴![]() =
=![]() .∴
.∴![]() =
= ![]() .∴b=
.∴b=![]() a.答案:C.
a.答案:C.
13. ![]() .底面正方形面积
.底面正方形面积![]() ,底面边长
,底面边长![]() ,高
,高![]() ,二面角的余切值
,二面角的余切值![]() .代入数据,得:
.代入数据,得:![]() .又
.又![]() 必为锐角,所以
必为锐角,所以 ![]() .
.
14.![]() .不妨认为一个正四棱柱为正方体,与正方体的所有面成角相等时,为与相交于同一顶点的三个相互垂直的平面所成角相等,即为体对角线与该正方体所成角.故
.不妨认为一个正四棱柱为正方体,与正方体的所有面成角相等时,为与相交于同一顶点的三个相互垂直的平面所成角相等,即为体对角线与该正方体所成角.故![]() .
.
15.![]() .
.
![]()
16. ①③④⑤. 如图,B、D、A1到平面![]() 的距离分别为
的距离分别为
1、2、4,则D、A1的中点到平面![]() 的距离为3,所
的距离为3,所
以D1到平面![]() 的距离为6;B、A1的中点到平面
的距离为6;B、A1的中点到平面![]() 的
的
距离为![]() ,所以B1到平面
,所以B1到平面![]() 的距离为5;则D、B的
的距离为5;则D、B的
中点到平面![]() 的距离为
的距离为![]() ,所以C到平面
,所以C到平面![]() 的距离
的距离
为3;C、A1的中点到平面![]() 的距离为
的距离为![]() ,所以C1到平面
,所以C1到平面![]() 的距离为7;而P为C、
的距离为7;而P为C、
C1、B1、D1中的一点,所以填①③④⑤.
17.法一:连接![]() ,
,
![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角.
所成的角.
 连接
连接![]() ,在△
,在△![]() 中,
中,
![]() ,
,
则![]()
![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
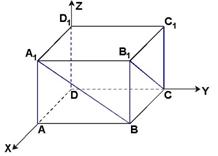
法二:以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
则 ![]() ,
,
得 ![]() .
.
 设
设![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
则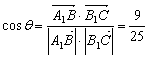 ,
,
![]()
![]() 与
与![]() 的夹角大小为
的夹角大小为![]() ,
,
即异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为
![]() .
.
18.(1)AM = MB = MN,说明NM是△ANB的中线且为边AB的一半,所以△ANB是直
角三角形,其中![]() ANB为直角。所以BN
ANB为直角。所以BN![]() NA。①
NA。①
![]() 且MN
且MN![]()
![]()
![]()
![]() 面ABN
面ABN![]()
![]() BN。②
BN。②
由①、②可推出BN![]() 面NAC。所以AC
面NAC。所以AC![]() BN。
BN。
(2)MN![]() AB且M为AB中点
AB且M为AB中点![]() AN = MN ③
AN = MN ③
 由(1)知,AN、BN、CN两两垂直 ④
由(1)知,AN、BN、CN两两垂直 ④
由③、④ ![]() AC = BC,又
AC = BC,又![]() ACB =
ACB = ![]() ,所以△ABC
,所以△ABC
是等边三角形。
设BN长度为1,则AB = ![]() ,
,
![]()
三棱锥![]() 的体积为:
的体积为:![]() ;
;
三棱锥![]() 的体积为:
的体积为:![]()
由![]() 可得 点N到面ABC的距离
可得 点N到面ABC的距离![]()
记NB与平面ABC所成角为![]() ,则
,则![]() 。
。
从而![]()
实际上,这个题的命题背景是![]() 是正方体的一个“角”。如图3.
是正方体的一个“角”。如图3.
19. 法一:(1)连AC,设AC与BD相交于点O,AP与平面
![]() 相交于点,,连结OG,因为
相交于点,,连结OG,因为 PC∥平面
PC∥平面![]() ,
,
平面![]() ∩平面APC=OG,
∩平面APC=OG,
故OG∥PC,所以,OG=![]() PC=
PC=![]() .
.
又AO⊥BD,AO⊥BB1,所以AO⊥平面![]() ,
,
故∠AGO是AP与平面![]() 所成的角.
所成的角.
在Rt△AOG中,tan![]() AGO=
AGO=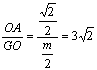 ,即m=
,即m=![]() .
.
所以,当m=![]() 时,直线AP与平面
时,直线AP与平面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.
(2)可以推测,点Q应当是AICI的中点O1,因为
D1O1⊥A1C1, 且 D1O1⊥A1A ,所以 D1O1⊥平面ACC1A1,
又AP![]() 平面ACC1A1,故 D1O1⊥AP.
平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直。
法二:(1)建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),P(0,1,m),C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1)
所以![]()
 又由
又由![]() 知,
知,![]() 为
为
平面![]() 的一个法向量.
的一个法向量.
设AP与平面![]() 所成的角为
所成的角为![]() ,则
,则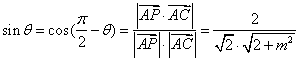 依题意有
依题意有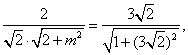 解得
解得![]() .故当
.故当![]() 时,直线AP与平面
时,直线AP与平面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.
(2)若在A1C1上存在这样的点Q,设此点的横坐标为![]() ,则Q(x,1-
,则Q(x,1-![]() ,1),
,1),![]() 。依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP,等价于D1Q⊥AP
。依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP,等价于D1Q⊥AP![]() 即Q为A1C1的中点时,满足题设要求.
即Q为A1C1的中点时,满足题设要求.
20. (理)(1)证明:以A为原点,分别以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系.
则A(0,0,0),B(a,0,0),M(![]() ,0,0),N(
,0,0),N(![]() ,
,![]() ,
,![]() ).
).
![]() =(a,0,0),
=(a,0,0),![]() =(0,
=(0,![]() ,
,![]() ).
).
![]() ·
·![]() =0
=0![]() AB⊥MN.
AB⊥MN.
(2)P(0,0,c),C(a,b,0),![]() =(a,b,-c),若MN是PC、AB的公垂线段,则
=(a,b,-c),若MN是PC、AB的公垂线段,则![]() ·
·![]() =0,即-
=0,即-![]() +
+![]() =0
=0![]() b=c.
b=c.
|
CD⊥DA
∴∠PDA是二面角P—CD—A的平面角.
∴∠PDA=45°,
即二面角P—CD—A是45°.
(文)(1)如图,以D为原点,DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系,取正方体棱长为2,则P(0,0,1)、M(2,1,0)、B(2,2,0)、B1(2,2,2).
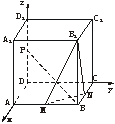
∵![]() ·
·![]() =(2,2,-1)·(0,1,2)=0,
=(2,2,-1)·(0,1,2)=0,
∴MB1⊥PB,同理,知NB1⊥PB.
∵MB1∩NB1=B1,∴PB⊥平面MNB1.
(2)∵PB⊥平面MNB1,BA⊥平面B1BN,∴![]() =(2,2,-1)与
=(2,2,-1)与![]() =(0,2,0)所夹的角即为α,cosα=
=(0,2,0)所夹的角即为α,cosα=![]() =
=![]() .
.
21. (1)EF分别为正方形ABCD得边AB、CD的中点,![]() EB//FD,且EB=FD,
EB//FD,且EB=FD,
![]() 四边形EBFD为平行四边形.
四边形EBFD为平行四边形.![]() BF//ED
BF//ED
![]()
![]()
![]() 平面
平面![]() .
.
(2)法一:如右图,点A在平面BCDE内的射影G在直线EF上,
过点A作AG垂直于平面BCDE,垂足为G,连结GC,GD.![]()
![]() ACD为正三角形,
ACD为正三角形,
![]() AC=AD
AC=AD![]() CG=GD
CG=GD ![]() G在CD的垂直平分线上,
G在CD的垂直平分线上,
![]() 点A在平面BCDE内的射影G在直线EF上,
点A在平面BCDE内的射影G在直线EF上,
过G作GH垂直于ED于H,连结AH,则![]() ,所以
,所以![]() 为二面角A-DE-C的平面角.即
为二面角A-DE-C的平面角.即![]()
设原正方体的边长为2a,连结AF
在折后图的![]() AEF中,AF=
AEF中,AF=![]() ,EF=2AE=2a,
,EF=2AE=2a,
即![]() AEF为直角三角形,
AEF为直角三角形, ![]()
![]()
在Rt![]() ADE中,
ADE中, ![]()
![]()
![]()
![]() .
.
法二:点A在平面BCDE内的射影G在直线EF上
连结AF,在平面AEF内过点作![]() ,垂足为
,垂足为![]() .
.
![]()
![]() ACD为正三角形,F为CD的中点,
ACD为正三角形,F为CD的中点,
![]()
又因![]() , 所以
, 所以![]()
![]()
![]()
又![]() 且
且![]()
![]()
![]() 为A在平面BCDE内的射影G.
为A在平面BCDE内的射影G.
即点A在平面BCDE内的射影在直线EF上
过G作GH垂直于ED于H,连结AH,则![]() ,所以
,所以![]() 为二面角A-DE-C的平面角.即
为二面角A-DE-C的平面角.即![]() 设原正方体的边长为2a,连结AF
设原正方体的边长为2a,连结AF
在折后图的![]() AEF中, AF=
AEF中, AF=![]() ,EF=2AE=2a,
,EF=2AE=2a,
即![]() AEF为直角三角形,
AEF为直角三角形, ![]()
![]()
在Rt![]() ADE中,
ADE中, ![]()
![]()
![]()
![]() .
.
法三: 点A在平面BCDE内的射影G在直线EF上
连结AF,在平面AEF内过点作![]() ,垂足为
,垂足为![]() .
.
![]()
![]() ACD为正三角形, F为CD的中点,
ACD为正三角形, F为CD的中点,
![]() 又因
又因![]() , 所以
, 所以![]()
![]()
![]()
又![]()
![]()
![]()
![]() 为A在平面BCDE内的射影G.
为A在平面BCDE内的射影G.
即点A在平面BCDE内的射影在直线EF上
过G作GH垂直于ED于H,连结AH,则![]() ,所以
,所以![]() 为二面角A-DE-C的平面角.即
为二面角A-DE-C的平面角.即![]() 设原正方体的边长为2a,连结AF
设原正方体的边长为2a,连结AF
在折后图的![]() AEF中,AF=
AEF中,AF=![]() ,EF=2AE=2a,
,EF=2AE=2a,
即![]() AEF为直角三角形,
AEF为直角三角形, ![]()
![]()
在Rt![]() ADE中,
ADE中, ![]()
![]()
![]() ,
, ![]() .
.
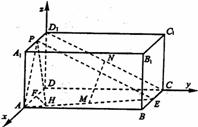 22. 法一:以D为原点,DA,DC,DD1所在直线分别
22. 法一:以D为原点,DA,DC,DD1所在直线分别
为x轴,y轴,z轴,建立空间直角坐标系D─xyz,
则A(a,0,0)、B(a,2a,0)、C(0,2a,0)、A1(a,0,a)、
D1(0,0,a) ∵E、P分别是BC、A1D1的中点,M、
N分别是AE、CD1的中点,
∴E(![]() ),P(
),P(![]() ),M(
),M(![]() ) ,N(
) ,N(![]() )
)
(1) ![]() ,取
,取![]() ,显然
,显然![]() ⊥面ADD1A1
⊥面ADD1A1![]() 而
而![]() ,∴
,∴![]() .又∴MN
.又∴MN![]() 面ADD1A1, ∴MN∥面ADD1A1;
面ADD1A1, ∴MN∥面ADD1A1;
(2)过P作PH⊥AE,交AE于H.取AD的中点F,则F![]() ,设H(x,y,0),
,设H(x,y,0),
则![]() ,
,![]() .
.
又![]() ,由
,由![]() 以及H在直线AE上可得:
以及H在直线AE上可得: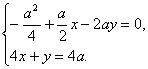
解得x=![]() ,y=
,y=![]() .∴
.∴![]()
![]() ,
,
所以![]() 即
即![]() ,∴
,∴![]() 与
与![]() 所夹的角等于二面角P─AE─D的大小.
所夹的角等于二面角P─AE─D的大小.![]() ,
,
所以二面角P─AE─D的大小![]() .
.
(3)设![]() 为平面DEN的法向量,
为平面DEN的法向量,
![]()
又![]() ,
,![]() ,
,![]()

∴P点到平面DEN的距离为d=![]()
∵![]() ,
,![]() ,
,
![]() .
.
所以![]() .
.
法二: (1)证明:取![]() 的中点
的中点![]() ,连结
,连结![]()
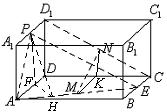 ∵
∵![]() 分别为
分别为![]() 的中点
的中点
∵![]()
∴![]() 面
面![]() ,
,![]() 面
面![]()
∴面![]() 面
面![]()
∴![]() 面
面![]()
(2)设![]() 为
为![]() 的中点
的中点
∵![]() 为
为![]() 的中点
∴
的中点
∴![]()
∴![]() 面
面![]()
作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,则由三垂线定理得
,则由三垂线定理得![]()
从而![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,从而
,从而
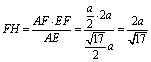 .
.
在![]() 中,
中,![]()
故:二面角![]() 的大小为
的大小为![]()
(3)![]() .
.
作![]() ,交
,交![]() 于
于![]() ,由
,由![]() ,得
,得![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
欢迎访问 http://www.k12zy.com