江苏省扬州中学2006-2007学年度第二学期开学考试
高三数学试卷 2007.2
一.选择题:(本大题共10小题,每小题5分,计50分)
1.两个非空集合![]() 和
和![]() ,它们都是全集
,它们都是全集![]() 的子集,满足
的子集,满足![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() 是指( )
是指( )
A.![]() 中至少有一个不是0
B.
中至少有一个不是0
B.![]() 且
且![]()
C.![]() 或
或![]() D.
D. ![]() 不都是0
不都是0
3.某人5次上班途中所花的时间(单位:分钟)分别为![]() ,10,11,9.已知这组数据的平均数为10,方差为2,则
,10,11,9.已知这组数据的平均数为10,方差为2,则![]() 的值为( )
的值为( )
A.1 B.2 C.3 D.4
4.设a、b、c分别是△ABC中∠A、∠B、∠C所对边的边长,则直线![]() 与
与![]() 的位置关系是( )
的位置关系是( )
A.平行 B.重合 C.垂直 D.相交但不垂直
5.已知函数![]() ,如果当
,如果当![]() 时,有
时,有![]() ,则实数
,则实数![]() 等于( )
等于( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
6.
已知: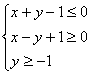 且
且![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在数列![]() 中,
中,![]() ,则
,则![]() 为( )
为( )
A.34 B.36 C.38 D.40
8.设![]() ,那么
,那么![]() 的最小值是( )
的最小值是( )
A.2 B.3 C.4 D.5
9.正方体![]() 的棱长为
的棱长为![]() ,在正方体表面上与点
,在正方体表面上与点![]() 距离是
距离是![]() 的点形成一条曲线,这条曲线的长度是 ( )
的点形成一条曲线,这条曲线的长度是 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10.动点P为椭圆![]() 上异于椭圆顶点
上异于椭圆顶点![]() 的一点,F1、F2为椭圆的两个焦点,动圆C与线段F1P的延长线、F1F2的延长线及线段PF2相切,则圆心C的轨迹为除去坐标轴上的点的( )
的一点,F1、F2为椭圆的两个焦点,动圆C与线段F1P的延长线、F1F2的延长线及线段PF2相切,则圆心C的轨迹为除去坐标轴上的点的( )
A.一条直线 B.双曲线的右支 C.抛物线 D.椭圆
二.填空题:(本大题共6小题,每小题5分,计30分)
11.若指数函数![]() 的部分对应值如下表:
的部分对应值如下表:
|
| -2 | 0 | 2 |
|
| 0.694 | 1 | 1.44 |
则不等式![]() 的解集为
.
的解集为
.
12.有一解三角形的题因纸张破损有一个条件不清,具体如下:在![]() 中,已知
中,已知![]() , ,求角
, ,求角![]() .经推断破损处的条件为三角形一边的长度,且答案提示
.经推断破损处的条件为三角形一边的长度,且答案提示![]() ,试将条件在横线处补全.
,试将条件在横线处补全.
13.设![]() 展开式中的各项系数之和为
展开式中的各项系数之和为![]() ,而它的二项式系数之和为
,而它的二项式系数之和为![]() ,若
,若![]() ,那么展开式中
,那么展开式中![]() 的系数为
.
的系数为
.
14.设![]() .若
.若![]() 是函数
是函数![]() 的单调递增区间,将
的单调递增区间,将![]() 的图象按向量
的图象按向量![]() 平移得到一个新的函数
平移得到一个新的函数![]() 的图象,则
的图象,则![]() 的单调递减区间必定为
.
的单调递减区间必定为
.
15.袋内有8个白球和2个红球,每次从中随机取出一个球,然后放回1个白球,则第4次恰好取完所有红球的概率为 .(用最简分数作答)
16.等差数列![]() 的前
的前![]() 项和为
项和为![]() ,公差
,公差![]() . 若存在正整数
. 若存在正整数![]() ,使得
,使得![]() ,则当
,则当![]() (
(![]() )时,有
)时,有![]() (填“>”、“<”、“=”).
(填“>”、“<”、“=”).
三.解答题:(本大题共5小题,第17、18小题每小题12分,第19题14分,第20、21题每小题16分,共计70分)
17. 已知向量![]() ,向量
,向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,且
,且![]() .
.
(Ⅰ)求向量![]() ;
;
(Ⅱ)设向量![]() ,向量
,向量![]() ,其中
,其中![]() ,
,
若![]() ,试求
,试求![]() 的取值范围.
的取值范围.
18.已知单调递增的等比数列![]() 满足
满足![]() ,且
,且![]() 是
是![]() 的等差中项.
的等差中项.
(Ⅰ)数列![]() 的通项公式;
的通项公式;
(Ⅱ)若![]() ,求使
,求使![]() 成立的正整数
成立的正整数![]() 的最小值.
的最小值.
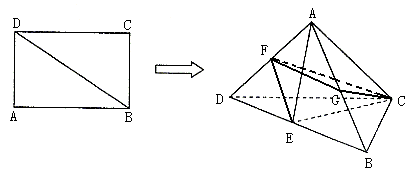
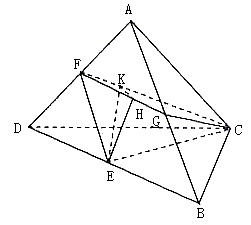
19.已知矩形ABCD中,![]() ,将ΔABD沿BD折起,使点A在平面BCD内的射影落在DC上,E、F、G分别为棱BD、AD、AB的中点.
,将ΔABD沿BD折起,使点A在平面BCD内的射影落在DC上,E、F、G分别为棱BD、AD、AB的中点.
(I)求证:DA⊥平面ABC;
(II)求点C到平面ABD的距离;
(III)求二面角G—FC—E的大小.
20.
点P在以![]() 为焦点的双曲线
为焦点的双曲线![]()
![]() 上,已知
上,已知![]() ,
,![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)求双曲线的离心率![]() ;
;
(Ⅱ)过点P作直线分别与双曲线渐近线相交于![]() 两点,且
两点,且![]() ,
,![]() ,求双曲线E的方程;
,求双曲线E的方程;
(Ⅲ)若过点![]() (
(![]() 为非零常数)的直线
为非零常数)的直线![]() 与(2)中双曲线E相交于不同于双曲线顶点的两点M、N,且
与(2)中双曲线E相交于不同于双曲线顶点的两点M、N,且![]() (
(![]() 为非零常数),问在
为非零常数),问在![]() 轴上是否存在定点G,使
轴上是否存在定点G,使![]() ?若存在,求出所有这种定点G的坐标;若不存在,请说明理由.
?若存在,求出所有这种定点G的坐标;若不存在,请说明理由.
21.已知函数![]() ,
,![]() ,和直线
,和直线![]() ,又
,又![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在![]() 的值,使直线
的值,使直线![]() 既是曲线
既是曲线![]() 的切线,又是
的切线,又是![]() 的切线;如果存在,求出
的切线;如果存在,求出![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
(Ⅲ)如果对于所有![]() 的
的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
命题:钱 伟
校对:姜卫东
江苏省扬州中学2006-2007学年度高三第二学期开学考试
数学试卷答题纸 2007.2
一、选择题:(每题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | B | D | C | D | B | C | C | D | A |
二、填空题:(每题5分,共30分)
11.![]() 12.
12.![]() 13.1
13.1
14. ![]() 15.
15.![]() 16.
16.![]()
三、解答题:(第17、18小题每小题12分,第19题14分,第20、21题每小题16分,共计70分)
17.解:(I)设![]() ,
,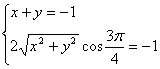 则
则![]() 或
或![]()
![]()
(II)![]()
![]()
![]()
![]() 。
。
18.解:(I)设![]() 的首项为
的首项为![]() 公比为
公比为![]() ,
,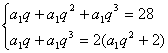
![]() ,
,![]()
![]() 单调递增
单调递增![]()
![]()
(II)![]() ,
,![]() ,由
,由![]()
有![]()
![]() 最小值为5。
最小值为5。
19.解:(I)证明:依条件可知DA⊥AB ①∵点A在平面BCD上的射影落在DC上,即平面ACD经过平面BCD的垂线∴平面ACD⊥平面BCD
又依条件可知BC⊥DC,∴BC⊥平面ACD,∵DA![]() 平面ACD∴BC⊥DA ②
平面ACD∴BC⊥DA ②
![]() ∴由①、②得DA⊥平面ABC
∴由①、②得DA⊥平面ABC
(II)解:设求点C到平面ABD的距离为d,于是![]()
由(I)结论可知DA⊥平面ABC∴DA是三棱锥D—ABC的高
∴由![]() ,得
,得![]() 解得
解得![]()
即点C到平面ABD的距离为![]() (或者证明CG⊥平面ABD,求CG的长即可)。
(或者证明CG⊥平面ABD,求CG的长即可)。
(III)解:由(I)结论可知DA⊥平面ABC∵AC、CG![]() 平面ABC
平面ABC
∴DA⊥AC ① DA⊥CG ②
由①得ΔADC为直角三角形,易求出AC=1,于是ΔABC中AC=BC=1
∵G是等腰ΔABC底边AB的中点∴CG⊥AB ③
![]() ④∴由②、③、④得CG⊥平面ABD
④∴由②、③、④得CG⊥平面ABD
∵CG![]() 平面FGC∴平面ABD⊥平面FGC在平面ABD内作EH⊥FG,垂足为H
平面FGC∴平面ABD⊥平面FGC在平面ABD内作EH⊥FG,垂足为H
∴EH⊥平面FGC,作HK⊥FC,垂足为K连结EK,故EK⊥FC
∴∠EKH为二面角E—FC—G的平面角
设RtΔABD边BD上的高为h,容易求出![]()
![]()
在ΔEFC中,容易求出![]()
 三边长满足
三边长满足![]() 于是在RtΔFEC中容易求出
于是在RtΔFEC中容易求出![]()
![]()
于是二面角E—FC—G的大小为![]()
20.解:(I)![]()
![]()
(II)![]() 渐近线为
渐近线为![]() 设
设![]()
![]() ,
,![]()
![]() 代入
代入![]() 化简
化简![]()
![]()
(III)假设在![]() 轴上存在定点
轴上存在定点![]() 使
使![]() ,
,
设![]() 联立
联立![]() 与
与![]() 的方程得
的方程得
![]() 故
故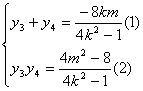
![]()
![]()
![]()
由![]()
![]()
![]()
∴(3)即为![]() ,将(4)代入(1)(2)
,将(4)代入(1)(2)
有![]() 代入(5)得
代入(5)得![]()
故在![]() 轴上存在定点
轴上存在定点![]() 使
使![]() 。
。
21.解:(Ⅰ)因为![]() ,所以
,所以![]() 即
即![]() ,所以a=-2.
,所以a=-2.
(Ⅱ)因为直线![]() 恒过点(0,9).
恒过点(0,9).
先求直线![]() 是y=g(x) 的切线.设切点为
是y=g(x) 的切线.设切点为![]() ,因为
,因为![]() .
.
所以切线方程为![]() ,将点(0,9)代入得
,将点(0,9)代入得![]() .
.
当![]() 时,切线方程为y=9, 当
时,切线方程为y=9, 当![]() 时,切线方程为y=12x+9.
时,切线方程为y=12x+9.
由![]() 得
得![]() ,即有
,即有![]()
当![]() 时,
时,![]() 的切线
的切线![]() ,
,
当![]() 时,
时, ![]() 的切线方程为
的切线方程为![]()
![]()
![]() 是公切线,
是公切线,
又由![]() 得
得![]()
![]()
![]() 或
或![]() ,
,
当![]() 时
时![]() 的切线为
的切线为![]() ,
,
当![]() 时
时![]() 的切线为
的切线为![]() ,
,![]()
![]() ,不是公切线
,不是公切线
综上所述
![]() 时
时![]() 是两曲线的公切线
是两曲线的公切线
(Ⅲ).(1)![]() 得
得![]() ,当
,当![]() ,不等式恒成立,
,不等式恒成立,![]() .
.
当![]() 时,不等式为
时,不等式为![]() ,
,
而![]()
![]()
![]()
当![]() 时,不等式为
时,不等式为![]() ,
,![]()
![]()
![]()
![]()
![]() 当
当![]() 时,
时,![]() 恒成立,则
恒成立,则![]()
(2)由![]() 得
得![]()
当![]() 时,
时,![]() 恒成立,
恒成立,![]() ,当
,当![]() 时有
时有![]()
设![]() =
=![]() ,
,
当![]() 时
时![]() 为增函数,
为增函数,![]() 也为增函数
也为增函数![]()
![]()
![]() 要使
要使![]() 在
在![]() 上恒成立,则
上恒成立,则![]()
由上述过程只要考虑![]() ,
,
则当![]() 时
时![]() =
=![]()
![]() 在
在![]() 时
时![]() ,在
,在![]() 时
时![]()
![]()
![]() 在
在![]() 时有极大值即
时有极大值即![]() 在
在![]() 上的最大值,又
上的最大值,又![]() ,即
,即![]() 而当
而当![]() ,
,![]() 时
时![]() ,
,![]()
![]() 一定成立
一定成立
综上所述![]() .
.