辽宁省沈阳市2007年高三教学质量监测(二)数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分共150分,考试时间120分钟.
注意事项:
1.答卷前将密封线内的项目和座位号填写清楚,将考号、座位号、考试科目用2B铅笔涂写在答题卡上。
2.答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试卷上。
3.考试结束,考生将试卷和答题卡上并交回。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]()
球的表面积公式![]() ,其中R表示球的半径.
,其中R表示球的半径.
球的体积公式![]() ,其中R表示球的半径.
,其中R表示球的半径.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合![]() ,则
,则![]() = ( )
= ( )
A.[0,2] B.[1,3] C.![]() D.
D.![]()
2.已知平面向量![]() ,则向量
,则向量![]() 与向量
与向量![]() 的夹角是 ( )
的夹角是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
|
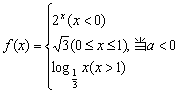 时,则
时,则 A.![]() B.
B.![]() C.-2 D.2
C.-2 D.2
5.教室里有30名同学,老师想把横、竖版两种答题卡各15张发给同学,每人一张,有( )种分法.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知![]() ,则
,则![]() 的值是 ( )
的值是 ( )
A.0 B.25 C.210 D.410
7.定义在R上的函数f(x)满足:f(x) = f (4-x)且f (2-x) + f (x-2) = 0,则f (2008)的值是( )
A.-1 B.0 C.1 D.无法确定
8.在△ABC中,给出下列四个命题:
①若![]() ,则△ABC必是等腰三角形;
,则△ABC必是等腰三角形;
②若![]() ,则△ABC必是直角三角形;
,则△ABC必是直角三角形;
③若![]() ,则△ABC必是钝角三角形;
,则△ABC必是钝角三角形;
④若![]() ,则△ABC必是等边三角形.
,则△ABC必是等边三角形.
以上命题中正确的命题的个数是 ( )
A.1 B.2 C.3 D.4
9.已知命题P:![]() ;命题Q:
;命题Q:![]() ,则P是Q的 ( )
,则P是Q的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
10.(理)已知双曲线![]() ,被方向向量为
,被方向向量为![]() 的直线截得的弦的中点为(4,1),则该双曲线离心率的值是 ( )
的直线截得的弦的中点为(4,1),则该双曲线离心率的值是 ( )
|
(文)定义运算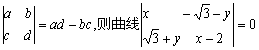 的切线方程中有一个是( )
的切线方程中有一个是( )
A.x-y = c B.x + y = 0 C.x = 0 D.y = 0
11.(理)在平在直角坐标系中,对于点(x,y)满足:“![]() ”,目标函数
”,目标函数
![]() ,那么满足z =-2的解(x,y)有( )个.
,那么满足z =-2的解(x,y)有( )个.
A.0 B.1 C.2 D.无数
(文)在平面直角坐标系中,对于点(x,y)满足:“![]() ”,那么使得目标函数z = x + y有最大值的解(x,y)有( )个.
”,那么使得目标函数z = x + y有最大值的解(x,y)有( )个.
A.0 B.1 C.2 D.无数
|
A.![]() B.
B.![]()
|
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在横线上.
13.(理)设a、![]() .
.
(文)在总体数为20的数据中抽出6个数据作为样本,这6个数据是2,2,3,3,4,4,那么用这6个数据估计总体的方差是 .
14.(理)已知点![]() 上一动点
上一动点![]() 的最小值是 .
的最小值是 .
(文)数列{an},a3 =
2,a7 = 1且数列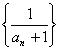 是等差数列,则a11 .
是等差数列,则a11 .
15.(理)在正方体ABCD—A1B1C1D1中,O1 上底面A1B1C1D1的中心,O是下底面ABCD的中心,则OB与CO所成角的余弦值为 .
(文)已知点![]() 上一动点
上一动点![]() 的最小值是 .
的最小值是 .
16.给出下列五个命题:
①函数![]() 的图象的对称中心是点(1,1);②函数
的图象的对称中心是点(1,1);②函数![]() 在第一象限内是增函数;③已知a,b,m均是正数,且
在第一象限内是增函数;③已知a,b,m均是正数,且![]() ;④若直线l∥平面α,直线l⊥直线m,直线
;④若直线l∥平面α,直线l⊥直线m,直线![]() ,则
,则![]() ;⑤当椭圆的离心率e越接近于0时,这个椭圆的形状就越接近于圆.
;⑤当椭圆的离心率e越接近于0时,这个椭圆的形状就越接近于圆.
其中正确命题的序号为 .
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤,解答过程书写在试卷中的对应空白处.
17.(本小题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,S是该三角形的面积,且
|
(1)求角A的大小;
(2)若角A为锐角,![]() ,求边BC上的中线AD的长.
,求边BC上的中线AD的长.
18.(本小题满分12分)
一个盒子装有六张卡片,上面分别写着如下六个定义域为R的函数:
![]()
(1)现从盒子中任取两张卡片,将卡片上的函数相加得一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中进行逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行.
(理)求抽取次数![]() 的分布列和数学期望.
的分布列和数学期望.
(文)求抽取次数不多于三次的概率.
19.(本小题满分12分)
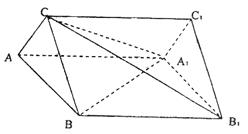
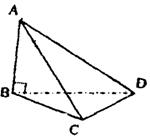
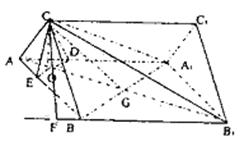
|
且AB = AA1 = 2,AC = 1.
(1)求证:A1B⊥CB1;
(2)求证:AC⊥平面CBA1;
(3)求二面角C—B1B—A的平面角的大小.
20.(本小题满分12分)
(理)设![]()
|
(2)设f(x)在[-1,1]上是单调函数,求a的取值范围.
(文)已知数列{an}中,![]()
(1)求证:数列{bn}为等比数列;
(2)若![]()
21.(本小题满分12分)
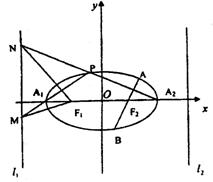
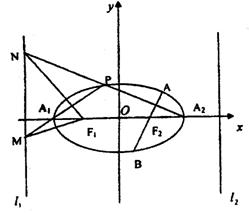
(理)如图所示,已知椭圆![]() 的焦距为2c,左右准线分别为l1、l2,长轴顶点为A1、A2,左右焦点分别为F1、F2.
的焦距为2c,左右准线分别为l1、l2,长轴顶点为A1、A2,左右焦点分别为F1、F2.
|
试判断以线段AB为直径的圆与椭圆右
准线l2的位置关系,并证明你的结论;
(2)过椭圆上任意纵坐标非零的点P作直线
PA1与PA2分别交l1于M、N两点.
求证:NF1⊥MF1.
(文)已知函数![]()
(1)要使f(x)在(0,2)上单调递增,试求a的取值范围;
(2)当a < 0时,若函数满足y极大值=1,y极小值=-3,试求函数y = f(x)的解析式;
(3)若![]() 时,y = f(x)图角上任意一点处的切线倾角为θ,求当
时,y = f(x)图角上任意一点处的切线倾角为θ,求当![]() 时,a的取值范围.
时,a的取值范围.
22.(本小题满分14分)
(理)已知函数![]() ,函数f(x)的图象与x轴有两个交点.
,函数f(x)的图象与x轴有两个交点.
(1)求a与b的值;
(2)若函数f(x)的导数为![]() ,数列{an}满足
,数列{an}满足![]() ,设
,设
![]() ,求数列{bn}的通项公式;
,求数列{bn}的通项公式;
(3)在(2)的条件下设![]() ,试孙函数g(x)在x =
1处的导数
,试孙函数g(x)在x =
1处的导数![]() ,并比较
,并比较![]() 的大小.
的大小.
(文)如图所示,已知椭圆![]() 的焦距为2c,左右准线分别为l1、l2,长轴顶点为A1、A2,左右焦点分别为F1、F2.
的焦距为2c,左右准线分别为l1、l2,长轴顶点为A1、A2,左右焦点分别为F1、F2.
(1)过右焦点F2作直线交椭圆于A、B两点,试判断以线段AB为直径的圆与椭圆右
准线l2的位置关系,并证明你的结论;
(2)过椭圆上任意纵坐标非零的点P作直线PA1与PA2分别交l1于M、N两点.
|
辽宁省沈阳市2007年高中三年级教学质量监测(二)
数学试题参考答案
|
1.D 2.D 3.A 4.B 5.A 6.C 7.B 8.B 9.B
|
二、填空题:本大题共4小题,每小题4分,共16分.
13.(理)-1 (文)![]() 14.(理)2 (文)
14.(理)2 (文)![]()
15.(理)![]() (文)2 16.③⑤
(文)2 16.③⑤
三、解答题:本大题共6小题,共74分.
17.(1)原式![]() …………………………2分
…………………………2分
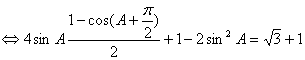
![]() …………………………4分
…………………………4分
因![]() …………………………………………………… 6分
…………………………………………………… 6分
(1)因A为锐角,则![]()
而面积![]() …………………8分
…………………8分
解法一:又由余弦定理![]() ,………………10分
,………………10分
又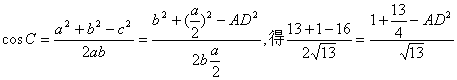 ,
,
即![]() ……………………………………………………………………12分
……………………………………………………………………12分
解法二:如图,作CE平行于AB,并延长AD交CE地E,
在△ACE中,![]()
又![]()
即![]()
这样![]() …………………………………………………………12分
…………………………………………………………12分
18.(理)解:(1)计事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,所以![]() ………………………………………………………………4分
………………………………………………………………4分
(2)(理)ξ可取1,2,3,4.
![]() ,
,
![]() ; …………8分
; …………8分
故ξ的分布列为
| ξ | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
……………………………………………………………10分
![]()
答:ξ的数学期望为![]() ………………………………………………………………12分
………………………………………………………………12分
(文)由已知抽取一次停止的概率为![]() , ………………………………6分
, ………………………………6分
抽取两次停止的概率为![]() ,………………………………………8分
,………………………………………8分
抽取三次停止的概率为![]() ,………………………………10分
,………………………………10分
所以抽取次数水多于三次的概率![]() …………12分
…………12分
|
过C作CO⊥平面BAA1B1于O,
作OD⊥AA1于D;OE⊥AB于E,
连接CD、CE,
则Rt△ADC≌Rt△AEC,即AE= AD,连结AD,
则Rt△AEO≌Rt△ADO,故∠EAO=∠OAD,
所以O在∠BAA1的平分线上. ………………2分
又AB=AA1,则平行四边形BAA1B1是菱形,
则O在AB1上,且A1B⊥AB1,
所以CB1在平面ABB1A1的射影是OB1,又A1B⊥AB1,则A1B⊥CB1,…………4分
(2)因AB=AA1=2,AC=1,∠BAA1=∠A1AC=∠CAB=60°,
在△ABC中BC=![]() ,则△ABC是直角三角形,即AC⊥BC,
,则△ABC是直角三角形,即AC⊥BC,
同理△AA1C是直角三角形,即AC⊥CA1,且CA1=![]() ,则AC⊥平面CBA1……8分
,则AC⊥平面CBA1……8分
(3)令A1B交AB1于G,则AC⊥CG,
即在Rt△ACG中,AC=1,AG=![]() ,则CO=
,则CO=![]() ,AO=
,AO=![]() ,
,
过O作OF⊥B1B于F,连结CF由(1)知OF是CF在平面ABB1A1内的射影,
则CF⊥BB1,所以在Rt△COF中∠CFO即是欲求二面角的平面角 ………………10分
又CO=![]() ,在Rt△OFB1中,OB1=
,在Rt△OFB1中,OB1=![]() ,sin∠OB1F=
,sin∠OB1F=![]() ,
,
则OF=![]() ,于是在Rt△COF中tan∠CFO=
,于是在Rt△COF中tan∠CFO=![]()
所以,二面角C—B1B—A的平面角的大小为![]() ……………………12分
……………………12分
20.(理)解(1)![]() ,
,
(1)当![]()
令![]() ;
;
令![]()
![]() 的极小值点的横坐标 ……………………………………………………3分
的极小值点的横坐标 ……………………………………………………3分
(2)当![]() ,
,
解得![]() ,
,
当x变化时,![]() 的变化情况如下表:
的变化情况如下表:
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) |
| 极大值 |
| 极小值 |
|
∴x1是极大值点的横坐标,x2是极小值点的横坐标 …………………………………6分
(2)因为f(x)在[-1,1]上是单调函数,
又![]()
即![]() 在[-1,1]上恒成立
……………………………8分
在[-1,1]上恒成立
……………………………8分
(1)当![]() ,显然成立 …………………………………………7分
,显然成立 …………………………………………7分
(2)当a<0时,则抛物线![]() 开口向下
开口向下![]()
即![]() ……………………………………………11分
……………………………………………11分
综上所述,a的取值范围是![]() ……………………………………………… 12分
……………………………………………… 12分
(文)(1)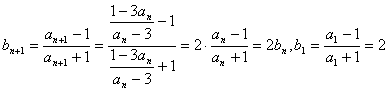 ,
,
∴{bn}为首项是2公比是2的等比数列 ……………………………………………6分
证明:(1)![]() ;
①
;
①
![]() ; ②……………………………8分
; ②……………………………8分
①-②得:![]() …………………………10分
…………………………10分
![]() …………………………………………………………………………11分
…………………………………………………………………………11分
![]() ………………………………………………………………12分
………………………………………………………………12分
21.(理)解:(1)设AB的中点为T,分别过点A,B,T作准线l1的垂线,垂足分别为
![]() 由椭圆的定义知,
由椭圆的定义知,
![]() ,
,
则![]() ,………………………… 4分
,………………………… 4分
![]() 所以以线段AB为直径的圆与椭圆右准线相离………6分
所以以线段AB为直径的圆与椭圆右准线相离………6分
(2)证明:设椭圆上任意一点![]() 椭圆的左焦点为
椭圆的左焦点为![]() ,
,
则直线PA2的方程为:![]() ,求得点N的坐标为
,求得点N的坐标为
![]() , ……………………………………………(7分)(文8分)
, ……………………………………………(7分)(文8分)
又直线PA1的方程为:![]() ,求得点M的坐标为
,求得点M的坐标为
![]() ,………………………………………………(8分)(文10分)
,………………………………………………(8分)(文10分)
则直线MF1的斜率![]() ,
,
![]()
…………………………(10分)(文12分)
因为点![]() ,所以
,所以
![]() ,所以NF1⊥MF1 …(12分)(文14分)
,所以NF1⊥MF1 …(12分)(文14分)
(文)解:(1)![]() ,要使f(x)在(0,2)上单调递增,
,要使f(x)在(0,2)上单调递增,
则![]() 在(0,2)上恒成立 …………………………………………………2分
在(0,2)上恒成立 …………………………………………………2分
即![]() …………………………………………… 4分
…………………………………………… 4分
(2)令![]()
![]() ,
,
![]() ,
,
![]() …………………………………………………………8分
…………………………………………………………8分
(3)![]() ,
,
![]() 上恒成立
上恒成立
由![]() ,
,
又![]() (当且仅当
(当且仅当![]() 时取“=”),
时取“=”),
![]() ,综上,a的取值范围是
,综上,a的取值范围是![]() ………………………………12分
………………………………12分
22.(理)解:(1)![]()
知![]() ,所以(1,0)是函数
,所以(1,0)是函数![]() 的图象与x轴的一个交点,由三次函数图象的性质,另一个交点必为极大值点,即
的图象与x轴的一个交点,由三次函数图象的性质,另一个交点必为极大值点,即![]() 由
由
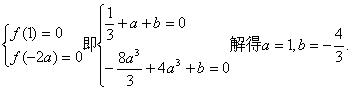 …………………………4分
…………………………4分
(2)由(1)知![]()
![]() ,
,
两边取对数![]() ,即
,即
![]() ,
,
所以数列{bn}是首项为2公比为2的等比数列,
则![]() ……………………………………………………………………………… 8分
……………………………………………………………………………… 8分
(3)![]()
![]()
![]() ①
①
![]() ②
②
②-①,得
![]() ,
,
![]() , ………………………………………………………………10分
, ………………………………………………………………10分
当![]() ;
;
当![]() ;
;
当![]() ;
;
当![]()
![]() ,
,
又![]() ,
,
所以![]() …………………………………………12分
…………………………………………12分
综上当![]() ;
;
当![]() …………………………………………………………14分
…………………………………………………………14分