重庆市南开中学高2007级3月月考试题
数 学(文科) 段泽文 录入
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
一、选择题:(本大题12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)。
1.设集合![]() ,
,![]() ,全集
,全集![]() ,则集合
,则集合![]() ( )
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2.已知![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
3.双曲线![]() 的渐进线方程为( )
的渐进线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
4.“p或q是假命题”是“非p为真命题”的( )
A. 充分而不必要条件 B.必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
5.在等比数列![]() 中,
中,![]() ,
,![]() ,
,![]() 成等差数列,则公比
成等差数列,则公比![]() 等于( )
等于( )
A. 1或2 B. ![]() 或
或![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
6.函数![]() 的反函数是( )
的反函数是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
7.室内有一根直尺,无论怎样放置,在地面上总有这样的直线,它与直尺所在的直线( )
A. 异面 B. 相交 C. 垂直 D. 平行
8.函数![]() 的图象在
的图象在![]() 处的切线与圆
处的切线与圆![]() 的位置关系为( )
的位置关系为( )
A. 相切B. 相交但不过圆心 C. 过圆心 D. 相离
9. 函数![]() 图解沿
图解沿![]() 轴向左平移
轴向左平移![]() 个单位,再将各点横坐标压缩为原来的
个单位,再将各点横坐标压缩为原来的![]() ,则所得函数是( )
,则所得函数是( )
A. 周期为![]() 的奇函数
B. 周期为
的奇函数
B. 周期为![]() 的偶函数
的偶函数
C. 周期为![]() 的奇函数
D. 周期为
的奇函数
D. 周期为![]() 的偶函数
的偶函数
10.已知三条不同的直线![]() 两个不同的平面
两个不同的平面![]() 。有下列命题:
。有下列命题:
①
![]() ②
② ![]()
③ ![]() ④
④![]()
其中正确的命题是( )
A. ①③ B. ②④ C. ①②④ D. ③
11.已知椭圆![]() 满足
满足![]() ,若离心率为
,若离心率为![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C.
![]() D. 4
D. 4
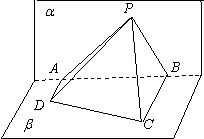 12. 如图,
12. 如图,![]() 所在的平面
所在的平面![]() 和四边形
和四边形![]() 所在的平面
所在的平面![]() 垂直,且
垂直,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,在平面
,在平面![]() 上有一个动点
上有一个动点![]() ,使得
,使得![]() ,则
,则![]() 在平面
在平面![]() 内的轨迹是( )
内的轨迹是( )
A. 圆的一部分
B. 椭圆的一部分
C. 双曲线的一部分
D. 抛物线的一部分
第Ⅱ卷(非选择题,共100分)
二、填空题:(本大题4个小题,每小题4分,共16分)各题答案必须填写在答题卡Ⅱ上只填结果,不要过程)。
13. 已知向量![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]()
14. 若实数![]() 满足
满足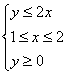 ,则
,则![]() 的最大值为__________
的最大值为__________
15. 已知正方体![]() ,直线
,直线![]() 所成角的正切值是_________
所成角的正切值是_________
16. 设![]() 上的点
上的点![]() ,在
,在![]() 处作曲线
处作曲线![]() 的切线与
的切线与![]() 轴交于
轴交于![]() ,过
,过![]() 作平行于
作平行于![]() 轴的直线与曲线
轴的直线与曲线![]() 交于
交于![]() ,然后在
,然后在![]() 处作曲线
处作曲线![]() 的切线与
的切线与![]() 轴交于
轴交于![]() ,过
,过![]() 作平行于
作平行于![]() 轴的直线与曲线
轴的直线与曲线![]() 交于
交于![]() ,依次类推,作出以下各点:
,依次类推,作出以下各点:![]() ,
,![]() ,…
,…![]() ,…,已知
,…,已知![]() ,则数列
,则数列![]() 的通项公式是_____________
的通项公式是_____________
三、解答题:(本大题6个小题,共76分)各题解答必需答在答题卡Ⅱ上(必需写出必要的文字说明、推理过程或计算步骤)
17.(13分)已知![]() 的三内角 ,且其对应边分别为
的三内角 ,且其对应边分别为![]() ,若向量
,若向量![]() ,
,![]() ,且
,且![]() 。
。
(1)求角![]() ;
;
(2)若![]() ,求
,求![]() 的面积。
的面积。
18.(13分)已知![]() 的图象与直线
的图象与直线![]() 垂直且在
垂直且在![]() 轴上的截距为3,
轴上的截距为3,
(1)求![]() 的解析式;
的解析式;
(2)设![]() ,解关于
,解关于![]() 的不等式
的不等式![]()
19.(12分)已知数列![]() 的前
的前![]() 项和
项和![]()
(1)求![]() ,
,![]() 及
及![]() 的通项公式;
的通项公式;
 (2)令
(2)令![]() ,问数列
,问数列![]() 的前多少项的和最大?
的前多少项的和最大?
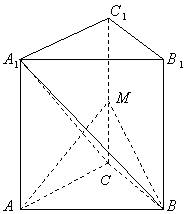
20.(12分)如图,在直三棱柱![]() 中,
中,![]() ,
,
![]() 为侧棱
为侧棱![]() 上一点,
上一点,![]() .
.
(1)求证:![]() ;
;
(2)求异面直线![]() 所成角的余弦值;
所成角的余弦值;
(3)求点![]() 到平面
到平面![]() 距离。
距离。
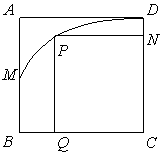 21.(12分)如图,
21.(12分)如图,![]() 是一块边长为
是一块边长为![]() 的正方形地域,地域内有一条河流
的正方形地域,地域内有一条河流![]() ,河流经过路线是以
,河流经过路线是以![]() 中点
中点![]() 为顶点且开口方向向右的抛物线(河流宽度忽略不计),其公司准备投资建一个大型矩形游乐园
为顶点且开口方向向右的抛物线(河流宽度忽略不计),其公司准备投资建一个大型矩形游乐园![]() ,问如何施工才能使游乐园面积最大,并求出最大值。
,问如何施工才能使游乐园面积最大,并求出最大值。
22. (12分)如图,设抛物线![]() 的焦点为
的焦点为![]() ,经过
,经过![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点坐标为
两点坐标为![]() ,
,![]() 是抛物线的准线上的一点,
是抛物线的准线上的一点,![]() 为坐标原点。
为坐标原点。
(1)求证:![]() ;
;
(2)若直线![]() 的方向向量分别为
的方向向量分别为![]() 求证:实数
求证:实数![]() 成等差数列;
成等差数列;
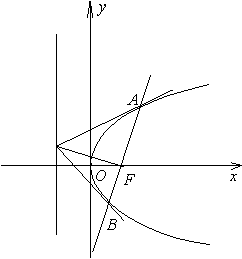
![]() (3)若
(3)若![]() ,求证:
,求证:![]()



