高2007届第一轮复习质量检测试题(2007.03.27)
数 学(理科) 段泽文 录入
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试时间120分钟。
第Ⅰ卷(选择题,共50分)
一、选择题:(本大题10个小题,每小题5分,共50分)各题答案必需答在答题卡上。
1.设集合![]() 全集
全集![]() ,则集合
,则集合![]() ( )
( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2. 已知![]() 则
则![]() 的值为( )
的值为( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
3. 在等比数列![]() 中,
中,![]() ,
,![]() ,
,![]() 成等差数列,则公比
成等差数列,则公比![]() 等于( )
等于( )
A. 1或2 B. ![]() 或
或![]() C.
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
4. 函数![]() 的反函数是( )
的反函数是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D. ![]()
5. 函数![]() 的图象在
的图象在![]() 处的切线与圆
处的切线与圆![]() 的位置关系为( )
的位置关系为( )
A. 相切B. 相交但不过圆心 C. 过圆心 D. 相离
6.下列极限中,其值为2的是( )
A. ![]()
B.
B. ![]()
C. ![]() D.
D.
![]()
|
A. 1个 B. 2个 C. 3个 D. 4个
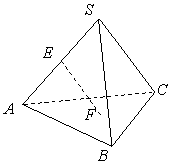 8.已知正四面体
8.已知正四面体![]() 中,点
中,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中心,则异面直线
的中心,则异面直线![]() 所成的角为( )
所成的角为( )
A. ![]()
B.
B. ![]()
C. ![]() D.
D.
![]()
9. 设定义域为![]() 函数
函数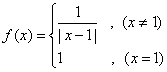 ,若关于
,若关于![]() 的方程
的方程 ![]() 有三个不同的实数解
有三个不同的实数解![]() ,则
,则![]() ( )
( )
A.5
B.![]() C.13
D.
C.13
D.![]()
10. 如图,![]() 所在的平面
所在的平面![]() 和四边形
和四边形![]() 平面
平面![]() 垂直,且
垂直,且![]() ,
,![]() ,
,![]()
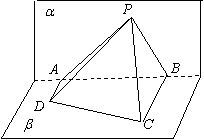
![]() ,
,![]() ,在平面
,在平面![]() 上有一个动点
上有一个动点![]() ,使得
,使得![]() ,则
,则![]() 在平面
在平面![]() 内的轨迹是( )
内的轨迹是( )
A. 圆的一部分
B. 椭圆的一部分
C. 双曲线的一部分
D. 抛物线的一部分
第Ⅱ卷(非选择题,共100分)
二、填空题:(本大题6个小题,每小题4分,共24分)各题答案必须填写在答题卡Ⅱ上(只填结果,不要过程)。
11.已知向量![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]()
12. 若实数![]() 满足
满足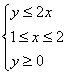 ,则
,则![]() 的最大值为__________
的最大值为__________
|
13.已知正方体![]() ,直线
,直线![]() 所成角的正切值是__________
所成角的正切值是__________
14.已知椭圆![]() 满足
满足![]() ,若离心率为
,若离心率为![]() ,则
,则![]() 的最小值为_______
的最小值为_______
15.若函数![]() 在
在![]() 上为减函数,则实数
上为减函数,则实数![]() 的取值范围是_________
的取值范围是_________
16.已知函数![]() ,令
,令![]() 表示坐标原点,
表示坐标原点,![]() ,若向量
,若向量![]() ,其中
,其中![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则![]() ___________
___________
三、解答题:(本大题6个小题,共76分)各题解答必需答在答题卡Ⅱ上(必需写出必要的文字说明、推理过程或计算步骤)。
17.(13分)已知![]() 的三内角 ,且其对应边分别为
的三内角 ,且其对应边分别为![]() ,若向量
,若向量![]() ,
,![]() ,且
,且![]() 。
。
(1)求角![]() ;(2)若
;(2)若![]() ,求
,求![]() 的面积。
的面积。
18.(13分)已知数列![]() 的前
的前![]() 项和
项和![]()
(1)求![]() 的通项公式;
的通项公式;
(2)令![]() ,问数列
,问数列![]() 的前多少项的和最大?
的前多少项的和最大?
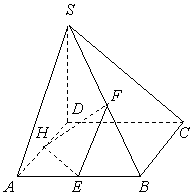
19.(13分)在四棱锥![]() 中,
中,![]() ,底面
,底面![]() 是正方形,
是正方形,![]()
![]() 分别是
分别是![]() 的中点。
的中点。
(1)证明:![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离。
的距离。
|
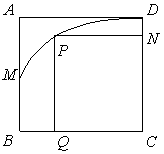 20.(13分)如图,
20.(13分)如图,![]() 是一块边长为
是一块边长为![]() 的正方形地域,地域内有一条河流
的正方形地域,地域内有一条河流![]() ,河流经过路线是以
,河流经过路线是以![]() 中点
中点![]() 为顶点且开口方向向右的抛物线(河流宽度忽略不计),其公司准备投资建一个大型矩形游乐园
为顶点且开口方向向右的抛物线(河流宽度忽略不计),其公司准备投资建一个大型矩形游乐园![]() ,问如何施工才能使游乐园面积最大,并求出最大值。
,问如何施工才能使游乐园面积最大,并求出最大值。
21.(12分)已知双曲线![]() 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为![]() ,点P的坐标为
,点P的坐标为![]() ,过点P的直线
,过点P的直线![]() 与双曲线C交于不同的两点
与双曲线C交于不同的两点![]() .
.
(1)求双曲线C的方程;
(2)设![]() ,求
,求![]() 的取值范围。
的取值范围。
22.(12分)已知函数![]() 上每一点处均可导的函数,若
上每一点处均可导的函数,若![]() 上恒立。
上恒立。
(1)证明:函数![]() 上是单调递增函数;
上是单调递增函数;
(2)用数学归纳法证明:对于任意的![]() 均有
均有
![]() 恒成立;
恒成立;
(3)已知不等式![]()
![]() 时恒成立,求证:
时恒成立,求证:
![]()
|



