07届高三数学4月第一次双周考试
命题人:倪伟华 审核人:赵颖颖 2007年4月9日
参考公式:一组数据x1,x2,…,xn的方差:
![]() 其中
其中![]() 为这组数据的平均数
为这组数据的平均数
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,恰有一项是符合题目要求的.
(1)“p或q为真命题”是 “p且q为真命题”的 ( )
(A)充分不必要条件 (B)必要非充分条件
(C)充要条件 (D)既不充分也不必要条件
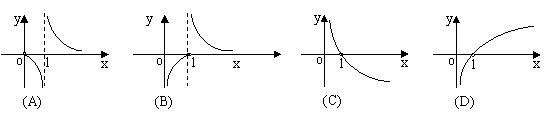 (2)函数f(x)=
(2)函数f(x)=![]() 的大致图象是 ( )
的大致图象是 ( )
(3)自圆x2+y2-2x-4y+4=0外一点P(0,4)向圆引两条切线,切点分别为A、B,则![]() 等于 ( )
等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
 (4)将函数
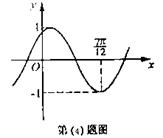
(4)将函数![]() 的图象按向量
的图象按向量![]() 平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(5)过抛物线y2=2px(p>0)的焦点F作直线交抛物线于A、B两点,O为原点,则△ABO的形状为 ( )
(A)直角三角形 (B)锐角三角形
(C)钝角三角形 (D)以上三种情况都有可能
(6)已知二次函数f(x)=ax2+bx+c,当x=1时有最大值1,若x∈[m,n](0<m<n)时,函数f(x)的值域为[![]() ,
,![]() ],则
],则![]() 的值为
( )
的值为
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(7)A,B,C,D,E五人住进编号为1,2,3,4,5的五个房间,每个房间只住一人,则B不住2号房间,且B,C两人不住编号相邻房间的住法种数为
( )
(A)24 (B)60 (C)70 (D)72
(8)已知等差数列{![]() }的前n项和为An,等差数列{bn}的前n项和为Bn,且
}的前n项和为An,等差数列{bn}的前n项和为Bn,且![]() =
=![]() ,(n∈N﹡)则使
,(n∈N﹡)则使![]() 为整数的所有n的值的个数为 ( )
为整数的所有n的值的个数为 ( )
(A) 2 (B)3 (C)4 (D)5
(9)为了稳定市场,确保农民增收,某农产品三月份以后的每月市场收购价格与其前三个月的市场收购价格有关,并使其与前三个月的市场收购价格之差的平方和最小,下表列出的是该产品今年前六个月的市场收购价格:
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 价格(元/担) | 68 | 78 | 67 | 71 | 72 | 70 |
则前七个月该产品的市场收购价格的方差为 ( )
(A)![]() (B)
(B)![]() (C)11
(D)
(C)11
(D)![]()
(10)已知C为线段AB上一点,P为直线AB外一点,满足![]() ,
,![]() ,
,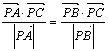 ,I为PC上一点,且
,I为PC上一点,且![]()
![]() ,则
,则![]() 的值为
( )
的值为
( )
(A) 1
(B) 2 (C) ![]() (D)
(D) ![]()
二、填空题:本大题共有6小题,每小题5分,共30分,不需写出解答过程,请把答案直接填写在答题卷相应位置上.
(11) 设z=3x+5y,式中的变量x、y满足约束条件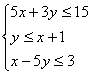 则z的
则z的
最大值为 .
(12)若不等式ax2+5x-2>0的解集是![]() ,则不等式
,则不等式
ax2-5x+(a2-1)>0的解集是 .
(13)已知![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]() ,若
,若![]() +…+
+…+![]() =
=![]() (
(![]() 且
且![]() ,那么
,那么![]() 的展开式中含
的展开式中含![]() 的项的系数是
的项的系数是
(14)正三棱锥的顶点都在同一个半径为R的球面上,球心到该棱锥底面的距离是球半径的一半,则该棱锥的体积是__________.
(15)在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是![]() ,且每次命中与否互相独立.
,且每次命中与否互相独立.
油罐被引爆的概率 .
至少需要射击4次才能引爆的概率 .
(16) 过双曲线M:![]() 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线![]() ,若
,若![]() 与双曲线M的两条渐近线分别相交于B、C,且AB=BC,则双曲线M的离心率是
与双曲线M的两条渐近线分别相交于B、C,且AB=BC,则双曲线M的离心率是
三、解答题:本大题共5小题,共70分,请在答题卷指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
(17) 在三角形ABC中,a、b、c分别是角A、B、C对边的长,且满足![]() .
.
(Ⅰ)求角B的值;
(Ⅱ)若b=![]() ,a+c=5,求a、c值.
,a+c=5,求a、c值.
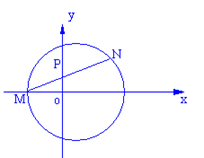 (18)如图,已知圆C:
(18)如图,已知圆C:![]() ,设
,设![]() 为圆C与
为圆C与![]() 轴左半轴的交点,过
轴左半轴的交点,过![]() 作圆C的弦
作圆C的弦![]() ,并使它的中点P恰好落在
,并使它的中点P恰好落在![]() 轴上。
轴上。
(1)
当![]() 时, 求满足条件的P点的坐标;
时, 求满足条件的P点的坐标;
(2)
![]() 当
当![]() 时,求N的轨迹G方程;
时,求N的轨迹G方程;
(3)过点P(0,2)的直线![]() 与(2)中轨迹G相交于两个不同的点
与(2)中轨迹G相交于两个不同的点![]() , 若
, 若![]() ,求直线
,求直线![]() 的斜率的取值范围。
的斜率的取值范围。
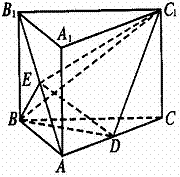 (19) 已知ABC—A1B1C1为正三棱柱,D是AC的中点(如图所示).
(19) 已知ABC—A1B1C1为正三棱柱,D是AC的中点(如图所示).
(1)证明:AB1∥平面DBC1.
(2)若AB1⊥BC1,BC=2.
①求二面角D—BC1—C的大小;
②若E为AB1的中点,求三棱锥E—BDC1的体积.
(20)已知函数f(x)=![]() .
.
(1)求f(x)的单调区间;
(2)求证:曲线y=f(x)在点![]() 处的切线恒过一定点,并求此定点的坐标;
处的切线恒过一定点,并求此定点的坐标;
(3)若![]() >
>![]() ,曲线y=f(x)在点(x1,f(x1))处的切线在x轴上的截距为x2,求
,曲线y=f(x)在点(x1,f(x1))处的切线在x轴上的截距为x2,求![]() 的取值范围.
的取值范围.
(21)设函数![]() 的定义域、值域均为
的定义域、值域均为![]() ,
,![]() 的反函数为
的反函数为![]() ,且对于任意实数
,且对于任意实数![]() ,均有
,均有![]() ,定义数列
,定义数列![]() :
:![]() .
.
(1)求证:![]() ;
;
(2)设![]() 求证:
求证:![]() ;
;
(3)是否存在常数![]() ,同时满足:①当
,同时满足:①当![]() 时,有
时,有![]() ;② 当
;② 当![]() .时,有
.时,有![]() 成立.如果存在满足上述条件的实数
成立.如果存在满足上述条件的实数![]() ,求出
,求出![]() 的值;如果不存在,证明你的结论。
的值;如果不存在,证明你的结论。
07届高三数学4月第一次双周考试参考答案
选择题:1.B 2.A 3.A 4.C 5.C 6.D 7.B 8.C 9.B 10.C
填空题:11.17
12.(-3,![]() ) 13.15 14.
) 13.15 14.![]()
15.![]() 16.
16.![]()
解答题:17.解:(Ⅰ)由正弦定律有:
![]()
代入![]()
即:2sinAcosB+sinCcosB+sinBcosC=0
2sinAcosB+sin(C+B)=0
在△ABC中,有A+B+C=π 即:sinA=sin(B+C)
∴2sinAcosB+sinA=0,
∵sinA≠0
∴cosB=-![]()
![]()
(Ⅱ)由余弦定律有:b2=a2+c22accosB=(a+c)2-2ac(1+cosB)
19=(5)2-2ac(1-![]()
![]()
18.解:(1)解法一:由已知得,![]() 时,可求得
时,可求得![]() 点的坐标为(-1,0),
点的坐标为(-1,0),
设P(0,b),则由![]() (或用勾股定理)得:
(或用勾股定理)得:![]() ,所以
,所以![]() 即点P坐标为
即点P坐标为![]() 。
解法二:同上可得
。
解法二:同上可得![]() ,设
,设![]() 则
则
![]() 解得
解得![]() 。所以
。所以![]() 的中点P坐标为
的中点P坐标为![]() 。
。
(2)解法一:设![]() 由已知得,在圆方程中令y=0,求得
由已知得,在圆方程中令y=0,求得![]() 点的坐标为
点的坐标为![]() 。设P(0,b),则由
。设P(0,b),则由![]() (或用勾股定理)得:
(或用勾股定理)得:![]() 。
。
因为点P为线段![]() 的中点,所以
的中点,所以![]() ,
,![]() ,又r>1
,又r>1
所以点N的轨迹方程为![]() 。
。
解法二:设N(x,y),同上可得![]() ,则
,则
![]() ,消去r,又r>1,所以点N的轨迹方程为
,消去r,又r>1,所以点N的轨迹方程为![]() 。
。
(3)设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
![]()
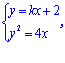 消去
消去![]()
![]() 因为直线
因为直线![]() 与抛物线
与抛物线![]() 相交于两个不同的点
相交于两个不同的点![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]()
综上可得![]() 。
。
19.(1)证明:连结CB1交BC1于O,连结OD.
∴OD∥AB1,OD在面DBC1内.∴AB1∥平面DBC1. 4分
(2)解:①OD⊥BC1,又O为BC1中点,∴DO=DC1.∴CC1=![]() .
.
过O作OM⊥BC1交BC于H,则OH=![]() ,∠HOD为所求.
,∠HOD为所求.
BH=![]() ,
,![]() ,∴cosθ=
,∴cosθ=![]() .∴θ45°. 8分
.∴θ45°. 8分
②![]()
20.(1) ![]() =
=![]() .
.
①当时,由![]() >0得x>
>0得x>![]() 或x<-
或x<-![]() ,从而此时f(x)在(
,从而此时f(x)在(![]() ,+∞),
,+∞),
(-∞,-![]() )上单调递增,在(-
)上单调递增,在(-![]() ,
,![]() )上单调递减;
)上单调递减;
②当a<0时![]() <0,此时f(x)在(-∞,+∞)上单调递减.
<0,此时f(x)在(-∞,+∞)上单调递减.
(2)易求切线方程为![]() ,切线恒过定点(0,-6);
,切线恒过定点(0,-6);
(3)曲线y=f(x)在点(x1,f(x1))处的切线方程为y-f(x1)= ![]() (x-x1),将点(x2,0)代入得:
(x-x1),将点(x2,0)代入得:
![]() ,设
,设![]() =
=![]() ,代入可分离出
,代入可分离出![]() ,有
,有![]() ,可得
,可得![]() .
.
21、.解:(1)由![]() ,得
,得![]() ,
,
又![]()
![]() ,令
,令![]() 得
得
![]() ,即
,即![]() ;---------------------------------4分
;---------------------------------4分
(2)![]() ,
,![]() ,即
,即![]() ,---------6分
,---------6分
又![]() ,
,
所以![]() ,
,
所以![]() -----------8分
-----------8分
(3)假设存在常数![]() ,使得当
,使得当![]() 时,有
时,有![]() ,则
,则![]() ,解得
,解得![]() 。
---------------------------10分
。
---------------------------10分
由![]() ,即
,即![]() ,
,
两边同时除以![]() ,得
,得![]() ,分别令
,分别令![]() 得
得
![]() ,
,![]() ,
,![]()
![]() ,--------13分
,--------13分
将这![]() 个不等式想加得
个不等式想加得![]()
![]() 。
。
即存在![]() ①当
①当![]() 时,有
时,有![]() ;
;
② 当![]() .时,有
.时,有![]() 成立.----------------------------16分
成立.----------------------------16分