|
数学(理科)试题 命题:
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 共150分,考试时间120分钟.
注意事项:
1.第Ⅰ卷的答案用2B铅笔涂在答题卡上,第Ⅱ卷的答案或解答过程均写在答题纸内的指定处,写在试题卷上的无效.
2.答题前,考生务必将自己的“班级”、“学号”、“姓名”写在答题卡和答题纸上.
3.考试结束后,只交答题卡和答题纸.
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的
1.集合![]()
![]() ,则
( )
,则
( )
A.![]()
![]() B.
B.![]()
C.![]() D.
D.![]() R
R
2.在复平面内,复数![]() 对应的点位于
( )
对应的点位于
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.![]() =
( )
=
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
4.如果![]() 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中![]() 的系数是 ( )
的系数是 ( )
A.7
B.![]() C.21
D.
C.21
D.![]()
5.设x,y满足不等式组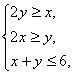 则z=3x-2y的最大值是
则z=3x-2y的最大值是
A.0 B.2 C.8 D.16
6.不等式![]() ( )A.(0,
( )A.(0,![]() B.(-∞,0)∪(0,
B.(-∞,0)∪(0,![]() ]
]
C.(-∞, ![]() )∪[1,3]
D.(-∞,0)∪(0,
)∪[1,3]
D.(-∞,0)∪(0, ![]() )∪[1,3]
)∪[1,3]
7.设函数![]() 的最大值为3,则f(x)的图象的一条对称轴的方程是 ( )
的最大值为3,则f(x)的图象的一条对称轴的方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.对于直线![]() 、
、![]() 和平面
和平面![]() 、
、![]() ,
,![]() ∥
∥![]() 的一个充分不必要条件是
( )
的一个充分不必要条件是
( )
A. ![]() ∥
∥![]() ,
,![]() ∥
∥![]() B.
B. ![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,![]() ∥
∥![]()
C. ![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() D.
D. ![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]()
9.从一块短轴长为2![]() 的椭圆形玻璃镜中划出一块矩形,其面积的最大值在
的椭圆形玻璃镜中划出一块矩形,其面积的最大值在![]() 内,则这一椭圆离心率e的取值范围是 ( )
内,则这一椭圆离心率e的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.一次研究性课堂上,老师给出函数![]() ,三位同学甲、乙、丙在研究此函数时分别给出命题:
,三位同学甲、乙、丙在研究此函数时分别给出命题:
甲:函数![]() 的值域为
的值域为![]() ;
;
乙:若![]() ,则一定有
,则一定有![]() ;
;
丙:若规定![]() ,则
,则![]() 对任意
对任意![]() 恒成立.
恒成立.
你认为上述三个命题中正确的个数有( )
A.0个 B.1个 C.2个 D.3个
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共5小题,每小题5分,共25分.
 11某展览会一周(七天)内要接待三所学校学生参观,每天至多安排一所学校,其中一所人数较多的学校要连续参观2天,其余学校均只参观1天,则在这一周内不同的安排方法数是 (用数字作答)。
11某展览会一周(七天)内要接待三所学校学生参观,每天至多安排一所学校,其中一所人数较多的学校要连续参观2天,其余学校均只参观1天,则在这一周内不同的安排方法数是 (用数字作答)。
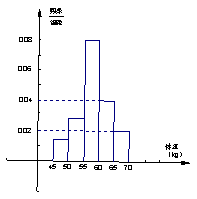
12.为了解某中学高一新生的体重情况,抽查了该中学1000名高一新生的体重(kg),得到频率分布直方图(如右图),根据右图可得这1000名学生中体重不小于60(kg)的学生人数是 .
13.过点(1,2)总可作两条直线与圆![]() 相切,则实数
相切,则实数![]() 的取值范围
的取值范围
是
14.在凸四边形ABCD中,AB=4,BC=3,![]() ,且
,且![]() ,则
,则![]() 等于
等于
15.将正方形ABCD沿对角线BD折成直二面角A—BD—C,有如下四个结论:
①AC⊥BD; ②△ACD是等边三角形;
③AB与平面BCD所成的角为60° ④AB与CD所成的角为60°
其中正确结论的序号是 .(写出所有你认为正确的结论的序号)
三、解答题:本大题共6小题,共75分.解答应写出必要的文字说明、证明过程或演算步骤.
16.(本小题满分12分)
已知△ABC的三个内角A、B、C的对边分别为a、,b、c,若a、b、c成等差数列,且![]() ,求角B的大小,并判断△ABC的形状。
,求角B的大小,并判断△ABC的形状。
17.(本小题满分12分)已知数列![]() 满足递推关系式
满足递推关系式
![]()
(Ⅰ)求![]()
| |
(Ⅲ)求数列![]() 的前n项和Sn.
的前n项和Sn.
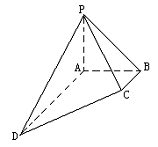
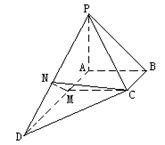
18.(本小题满分12分)
|
∠ABC=![]() ,
,![]() ,
,![]() .
.
(Ⅰ) 求点D到平面PBC的距离;
(Ⅱ) 求二面角![]() 的大小.
的大小.
19.(本小题满分12分)一种玩掷骰子放球游戏的规则是:若掷出1点,则在甲盒中放一球;若掷出2点或3点,则在乙盒中放一球;若掷出4点、5点或6点,则在丙盒中放一球。设掷三次后,甲、乙、丙盒内的球数分别是x,y,z。
(I)求随机变量y的分布列及数学期望;
(II)证明:Ex,Ey,Ez成等差数列。
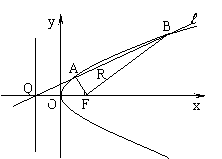
20.(本小题满分13分)
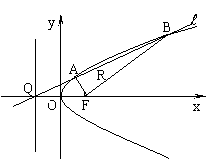
如图,![]() 是抛物线
是抛物线![]() 的焦点,
的焦点,![]() 是准线与
是准线与![]() 轴的交点,直线
轴的交点,直线![]() 经过点
经过点![]() 。
。
(1) 直线![]() 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求![]() 的方程;
的方程;
(2) 直线![]() 与抛物线交于A,B两点,
与抛物线交于A,B两点,
(Ⅰ)记![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹方程。
的轨迹方程。
 |
21.(本小题满分14分)已知函数![]()
(1) 若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2) 若定义在区间D上的函数![]() 对于区间D上的任意两个值
对于区间D上的任意两个值![]() 总有以下不等式
总有以下不等式![]() 成立,则称函数
成立,则称函数![]() 为区间D上的“凹函数”.
为区间D上的“凹函数”.
试证判断当![]() 时,
时,![]() 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
宜昌市2007届高三年级三月调研考试数学(理)试题参考答案
一.选择题 BCCCC DACAD
二. 填空题
11. 120 12.300 13.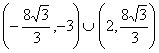 14.
14. ![]()
15.(1)(2)(4)
三.解答题
16.解:![]() ,
,![]() 分
分
![]() ,
,![]() 或
或![]() (舍)………………4分
(舍)………………4分
![]() ……………6分,又
……………6分,又![]() 成等差数列,
成等差数列,![]() ,……7分
,……7分
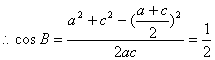 ……9分, 化简得
……9分, 化简得 ![]() ,………11分
,………11分
![]() 是正三角形…………………………12分
是正三角形…………………………12分
另,边化角也可,略。
17.解:(1)由![]() 知
知![]()
解得:![]() 同理得
同理得![]() ……………………3分
……………………3分
(2)![]()
![]()
![]()
即![]() 构成以
构成以![]() 为首项,以1为公差的等差数列,……………………6分
为首项,以1为公差的等差数列,……………………6分
![]() ,
,![]()
![]() …………………………8分
…………………………8分
(此问也可先猜,后用数学归纳法证明)
(3)![]()
![]()
![]()
![]()
![]() ………12分
………12分
18.解:(Ⅰ)如图,在四棱锥![]() 中,
中,
∵BC∥AD,从而点D到平面PBC间的距离等于点A到平面PBC的距离.
∵∠ABC=![]() ,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,
,∴AB⊥BC, 又PA⊥底面ABCD,∴PA⊥BC,
∴BC⊥平面 PAB,………………2分
∴平面PAB⊥平面PBC,交线为PB,过A作AE⊥PB,垂足为E,则AE⊥平面PBC,
∴AE的长等于点D到平面PBC的距离.而![]() ,∴
,∴![]() .………5分
.………5分
|
(Ⅱ) ∵PA⊥底面ABCD,∴平面PAD⊥底面ABCD,
引CM⊥AD于M,MN⊥PD于N,则CM⊥平面PAD,
∴MN是CN在平面PAD上的射影,
由三垂线定理可知CN⊥PD,
∴∠CNM是二面角![]() 的平面角.…………9分
的平面角.…………9分
依题意![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
可知![]() ,∴
,∴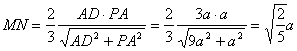 ,
,
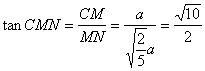 ,∴二面角
,∴二面角![]() 的大小为
的大小为![]() …… 12分
…… 12分
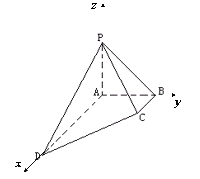
解法二:如图, A为原点,分别以AD、AB、AP为x轴、y轴、z轴建立空间直角坐标系.
|
∴![]() ,
,
∴![]() . 则
. 则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
设平面PBC的一个法向量为![]() ,则
,则
![]() 令
令![]() ,得
,得![]() ,
,
则点D到平面PBC的距离等于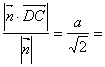
![]() .……………6分
.……………6分
(Ⅱ) ∵AB⊥PA,AB⊥AD,∴AB⊥底面PDA,∴平面PDA的一个法向量为![]() .
.
设平面PDC的一个法向量为![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]()
令![]() ,得
,得![]() ,∴
,∴![]() .
.
∵二面角![]() 是锐二面角,∴二面角
是锐二面角,∴二面角![]() 的大小为
的大小为![]() .……12分
.……12分
19.(Ⅰ)![]() 可能的值是
可能的值是![]() …1分
…1分
![]() …2分
…2分
![]() …3分
…3分
![]() …4分
…4分
![]() …5分
…5分
随机变量![]() 的分布列
的分布列
|
|
|
|
|
|
|
|
|
|
|
|
所以 ![]() …8分
…8分
(Ⅱ)由题意知
![]() , 所以
, 所以![]() …10分
…10分
即 ![]() 得
得 ![]()
故![]() 成等差数列。
…12分
成等差数列。
…12分
 20.解: 依题意
20.解: 依题意![]() ,直线
,直线![]() 斜率存在,设其斜率为
斜率存在,设其斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,代入抛物线方程有:
,代入抛物线方程有:![]() ……………2分
……………2分
(1)若![]() ,令
,令![]() 得,
得,![]() ,此时,
,此时,![]() 的方程为
的方程为![]() 。…………………4分
。…………………4分
若![]() ,方程有唯一解。此时方程为
,方程有唯一解。此时方程为![]() ………5分
………5分
(2)显然![]() ,记
,记![]() ,则
,则![]() ,
,![]() ,
,![]() ………7分
………7分
(Ⅰ)![]() ………………………9分
………………………9分
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() …………………11分 ∴
…………………11分 ∴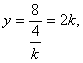
![]() ,………12分
,………12分
由![]() 得,
得,![]() ,又
,又![]() ,∴
,∴![]() 。
。
综上,点R的轨迹方程为![]()
![]() 。…………………………13分
。…………………………13分
21.解:(Ⅰ)由![]() ,得
,得![]() ……………………2分
……………………2分
欲使函数为![]() 上单调增函数,则
上单调增函数,则![]() 在
在![]() 上恒成立,即不等式
上恒成立,即不等式![]() 在
在![]() 上恒成立.也即
上恒成立.也即![]() 在
在![]() 上恒成立.………………4分
上恒成立.………………4分
令![]() ,上述问题等价于
,上述问题等价于![]() ,而
,而![]() 为在
为在![]() 上的减函数,则
上的减函数,则![]() ,于是
,于是![]() 为所求. …………………………………………………………6分
为所求. …………………………………………………………6分
(Ⅱ)证明:由![]() 得
得
![]()
![]() ……………………………………………………………………………7分
……………………………………………………………………………7分
![]() ………………………………………………………………8分
………………………………………………………………8分
而![]() ① ………………………………………10分
① ………………………………………10分
又![]() , ∴
, ∴![]() ② …………11分
② …………11分
∵![]() ∴
∴![]() ,
,
∵![]() ∴
∴![]() ③ ………………………………………………………13分
③ ………………………………………………………13分
由①、②、③得![]()
即![]() ,从而由凹函数的定义可知函数为凹函数. …………14分
,从而由凹函数的定义可知函数为凹函数. …………14分