2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(5)—《不等式》
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设![]() ,已知命题
,已知命题![]() ;命题
;命题![]() ,则
,则![]() 是
是![]() 成立的( )
成立的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
2.已知不等式![]() 对任意正实数
对任意正实数![]() 恒成立,则正实数
恒成立,则正实数![]() 的最小值为( )
的最小值为( )
A.8 B.6 C.4 D.2
3.(文)命题p:若a、b∈R,则a+b>1是a+b>1的充分而不必要条件; 命题q:函数y=![]() 的定义域是(-∞,-1
的定义域是(-∞,-1![]() ∪[3,+∞
∪[3,+∞![]() .则 ( )
.则 ( )
A.“p或q”为假 B.p假q真
C.p真q假 D.“p且q”为真
(理)设偶函数f (x)=logax-b在(-∞,0)上递增,则f (a+1)与f (b+2)的大小关系是( )
A.f(a+1)=f (b+2) B.f (a+1)>f (b+2)
C.f(a+1)<f (b+2) D.不确定
4.(文)若![]() ,则下列不等式 ①
,则下列不等式 ①![]() ;②
;②![]() ③
③![]() ;④
;④![]() 中,正确的不等式有 ( )
中,正确的不等式有 ( )
A.0个 B.1个 C.2个 D.3个
(理)某汽车运输公司,购买了一批豪华大客车投入营运,据市场分析每辆客车营运的总利润y(单位:10万元)与营运年数x的函数关系为![]() 则每两客车营运多少年,其运营的年平均利润最大 ( )
则每两客车营运多少年,其运营的年平均利润最大 ( )
A.3 B.4 C.5 D.6
5.(文)![]() 成立的 ( )
成立的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条
(理)对于![]() 的一切值,则
的一切值,则![]() 恒成立的 ( )
恒成立的 ( )
A.充要条件 B.充分非必要条件
C.必要非充分条件 D.既不充分也不必要条件
6.若a,b,c>0且a (a+b+c)+bc=4-2![]() ,则2a+b+c的最小值为 ( )
,则2a+b+c的最小值为 ( )
A.![]() -1 B.
-1 B. ![]() +1 C. 2
+1 C. 2![]() +2 D. 2
+2 D. 2![]() -2
-2
7. 设a、b、c是互不相等的正数,则下列等式中不恒成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.(文)实数满足![]() 则
则![]() 的值为 ( )
的值为 ( )
A.8 B.-8
C.8或-8
D.与![]() 无关
无关
(理)已知![]() 之间的大小关系是( )
之间的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 的关系随c而定
的关系随c而定
9.(文)若函数![]() 是奇函数,且在(
是奇函数,且在(![]() ),内是增函数,
),内是增函数,![]() ,则不等式
,则不等式![]() 的解集为 ( )
的解集为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(理)若![]() 是偶函数,且当
是偶函数,且当![]() 的解集是( )
的解集是( )
A.(-1,0) B.(-∞,0)∪(1,2)
C.(1,2) D.(0,2)
10.若不等式x2+ax+1³0对于一切xÎ(0,![]() )成立,则a的取值范围是 ( )
)成立,则a的取值范围是 ( )
A.0
B. –2
C.-![]() D.-3
D.-3
11.某商场的某种商品的年进货量为1万件,分若干次进货,每次进货的量相同,且需运费100元,运来的货物除出售外,还需租仓库存放,一年的租金按一次进货时的一半来计算,每件2元,为使一年的运费和租金最省,每次进货量应为 ( )
A.200件 B.5000件 C.2500件 D.1000件
12.不等式![]() 对满足
对满足![]() 恒成立,则
恒成立,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13.(文)b克盐水中,有a克盐(![]() ),若再添加m克盐(m>0)则盐水就变甜咸了,试根据这一事实提炼一个不等式 .
),若再添加m克盐(m>0)则盐水就变甜咸了,试根据这一事实提炼一个不等式 .
(理)已知三个不等式①ab>0 ② ![]() >
> ![]() ③bc>ad 以其中两个作条件余下一个作结论,则可组 个正确命题.
③bc>ad 以其中两个作条件余下一个作结论,则可组 个正确命题.
14.若记号“*”表示求两个实数a与b的算术平均数的运算,即a*b=![]() ,则两边均含有运算符号“*”和“+”,且对于任意3个实数,a、b、c都能成立的一个等式可以是_________.
,则两边均含有运算符号“*”和“+”,且对于任意3个实数,a、b、c都能成立的一个等式可以是_________.
15.设a>0,n![]() 1,函数f (x) =alg(x2-2n+1)
有最大值.则不等式logn(x2-5x+7)>0的解集为__
_.
1,函数f (x) =alg(x2-2n+1)
有最大值.则不等式logn(x2-5x+7)>0的解集为__
_.
16.已知![]() 则不等式
则不等式![]() ≤5的解集是
____ .
≤5的解集是
____ .
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)(文科做)比较下列两个数的大小:
(1)![]()
(2)![]() ;
;
(3)从以上两小项的结论中,你否得出更一般的结论?并加以证明
(理科做)已知:![]()
![]() ,
,
试比较M,N的大小:你能得出一个一般结论吗?
18.(本小题满分12分)已知实数P满足不等式![]() 判断方程
判断方程![]() 有
有
无实根,并给出证明.
19.(本小题满分12分)(文科做)关于x的不等式组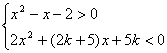 的整数解的集合为{-2},求实质数k的取值范围.
的整数解的集合为{-2},求实质数k的取值范围.
(理科做)若![]() 是定义在
是定义在![]() 上的增函数,且对一切
上的增函数,且对一切![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 解不等式
解不等式![]() .
.
20.(本小题满分12分)某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
(1)把房屋总造价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?
21.(本小题满分12分)(文科做)设![]()
求证:![]()
(理科做)设![]()
(1)证明A>![]() ;
;
(2)![]()
22. (本小题满分14分)(2006年广东卷)A是由定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:①对任意
组成的集合:①对任意![]() ,都有
,都有![]() ; ②存在常数
; ②存在常数![]() ,使得对任意的
,使得对任意的![]() ,都有
,都有![]()
(1)设![]() ,证明:
,证明:![]() ;
;
(2)设![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,那么这样的
,那么这样的![]() 是唯一的;
是唯一的;
(3)设![]() ,任取
,任取![]() ,令
,令![]() 证明:给定正整数k,对任意的正整数p,成立不等式
证明:给定正整数k,对任意的正整数p,成立不等式![]() .
.
参考答案(5)
1.B.命题![]() 是命题
是命题![]() 等号成立的条件,故选B.
等号成立的条件,故选B.
2.C.恒成立的意义化为不等式求最值,
![]() ,验证,2不满足,4满足,选C.
,验证,2不满足,4满足,选C.
3.(文)B.命题p假,取a=-1,b=1可得;命题q真,由![]() 得
得
(理)B.由偶函数得![]() ,由函数递增性得
,由函数递增性得![]()
又![]()
![]() .
.
4.(文)C. ①正确,②错误,③错误,④正确.
(理)C. ![]()
5.(文)B.取x=2时![]() 不成立,充分性不正确,由
不成立,充分性不正确,由![]() 可推得
可推得![]() ,必要性正确
,必要性正确
(理)C. 取![]() 时
时![]() 取
取![]() 时
时![]() 充分性不成立,必要性成立由一次函数思想
充分性不成立,必要性成立由一次函数思想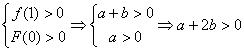
6.D.因为![]() ,故
,故![]() +4ab+4ac+2bc
+4ab+4ac+2bc![]() 4
4![]() +4ab+4ac+4bc
+4ab+4ac+4bc
= 4[a(a+b+c)+bc]=4[4-2![]() ],又a,b,c>0,故上式两边开方得,2a+b+c
],又a,b,c>0,故上式两边开方得,2a+b+c![]() =2
=2![]() =2
=2![]() -2,故选D.
-2,故选D.
7.C.因为![]() ,所以(A)恒成立;
,所以(A)恒成立;
在B两侧同时乘以![]() 得
得
![]() 所以B恒成立;
所以B恒成立;
在C中,当a>b时,恒成立,a<b时,不成立;
在D中,分子有理化得![]() 恒成立,故选C.
恒成立,故选C.
8.(文)A. 由条件![]() 取绝对值得8.
取绝对值得8.
(理)C. x =![]() ,y=
,y=![]() ,∴x<y.
,∴x<y.
9.(文)D.由题意作![]() 的图象由图象易得
的图象由图象易得![]()
(理)D.由题意作![]() 的图象由图象易得
的图象由图象易得![]()
10.C.设f(x)=x2+ax+1,则对称轴为x=![]() ,若
,若![]() ³
³![]() ,即a£-1时,则f(x)在〔0,
,即a£-1时,则f(x)在〔0,![]() 〕上是减函数,应有f(
〕上是减函数,应有f(![]() )³0Þ-
)³0Þ-![]() £x£-1
£x£-1
若![]() £0,即a³0时,则f(x)在〔0,
£0,即a³0时,则f(x)在〔0,![]() 〕上是增函数,应有f(0)=1>0恒成立,故a³0
〕上是增函数,应有f(0)=1>0恒成立,故a³0
若0£![]() £
£![]() ,即-1£a£0,则应有f(
,即-1£a£0,则应有f(![]() )=
)=![]() 恒成立,故-1£a£0. 综上,有-
恒成立,故-1£a£0. 综上,有-![]() £a,故选C .
£a,故选C .
11.D.设每次进x件费用为y由![]()
![]() 时
时![]() 最小
最小
12.D.变形![]() 则
则![]() .
.
13.(文)![]() .提示:由盐的浓度变大得.
.提示:由盐的浓度变大得.
(理)3个,由不等式性质得:
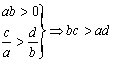
![]() ,
, 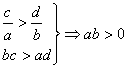
14.a+(b*c)=(a+b)*(a+c),(a*b)+c=(a*c)+(b*c),
a*(b+c)=(a+b)*c=(b+c)*a=(a+c)*b(a*b)+c=(b*a)+c等.
填出任何一个都行. 答案 不唯一.
提示:∵a+(b*c)=a+![]() =
=![]() =
=![]() = (a+b )*( a+c),其余类似可得
= (a+b )*( a+c),其余类似可得
15.![]() .由于f(x)有最大值,故0
.由于f(x)有最大值,故0![]() ,所以原不等式转化为0
,所以原不等式转化为0![]() -5x+7<1,
-5x+7<1,
又因为![]() 恒成立,故只需1
恒成立,故只需1![]() 成立即可,
成立即可,
解之得, ![]() .
.
16.![]() .分类⑴
.分类⑴![]() 原式成立 ⑵
原式成立 ⑵![]() 化为
化为![]() 综上得
综上得![]()
17.(文)(1)![]() ,(2)
,(2)![]()
(3)一般结论:若![]() 成立
成立
证明 欲证![]() 成立
成立
只需证![]()
也就是![]() (
(![]() )
)![]()
![]()
故![]()
![]()
(理)解先考查两个变量的情形
(1-a)(1-b)=1-a-b+ab≥1-a-b 当且仅当a、b中至少有1个为零时,等号成立
∴(1-a)(1-b)(1-c) ≥(1-a-b)(1-c)=1-a-b-c+c(a+b) ≥1-a-b-c 当且仅当a、b、c中至少有2个为零时,等号成立 于是(1-a)(1-b)(1-c)(1-d)≥1-a-b-c-d, 当且仅当a、b 、c、d 中至少有3个为零时,等号成立 ∴a、b、c、d至少有3个为0时,M=N,否则M>N .
18.解由![]()
![]()
方程![]() 的判别式
的判别式![]()
![]()
![]() ∴方程
∴方程![]() 无实根
无实根
19.(文)解:不等式![]() 的解集为
的解集为![]()
不等式![]() 可化为
可化为![]()
由题意可得![]()
![]() 不等式组的整数解的集合为{-2}
不等式组的整数解的集合为{-2} ![]() .
.
(理)(1)![]()
(2)![]()
![]() 即
即![]() 上的增函数
上的增函数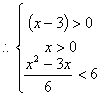
![]() .
.
20.(1)由题意可得,![]()
![]()
(2)![]() =13000
=13000
当且仅当![]() 即
即![]() 时取等号。
时取等号。
若![]() ,
,![]() 时,有最小值13000。
时,有最小值13000。
若![]() 任取
任取![]()
![]()
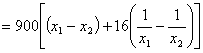
![]()
![]()
![]()
![]() 在
在![]() 上是减函数
上是减函数
![]() .
.
21.(文)![]()
![]()
![]()
![]()
![]() .
.
![]() 。
。
(理)(1)A![]()
=![]()
(2)![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]() ∴
∴![]()
22.解:对任意![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,所以
,所以![]() ,对任意的
,对任意的![]() ,
,
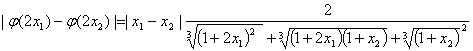 ,
,
![]()
![]() ,所以
,所以
0<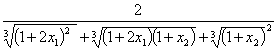
![]() ,令
,令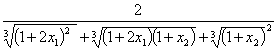 =
=![]() ,
,![]() ,
,
![]() ,所以
,所以![]() .
.
反证法:设存在两个![]() 使得
使得![]() ,
,![]() 则
则
由![]() ,得
,得![]() ,所以
,所以![]() ,矛盾,故结论成立。
,矛盾,故结论成立。
![]() ,所以
,所以![]()
![]()
![]()
![]()
![]() +…
+…
![]()
![]() .
.
欢迎访问 http://www.k12zy.com