张家港市后塍高级中学高三数学双周考测试卷
班级 学号 姓名
一、选择题（5*10=50分）
1、已知数列
，“对任意的
都在直线
上”是“为等差数列”的
（ ）
A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件
2．若函数f(x)＝loga(x2－ax＋3)在区间(－∞，]上为减函数，则a的取值范围是( )
A．(0，1) B．(1，＋∞)C．(1，2) D．(0，1)∪(1，2)
3．函数y＝－sinx＋cosx在x∈[－,]时的值域是 ( )
A．[0, ] B．[－,0] C．[0, ] D．[0,1]
４．已知点
在不等式组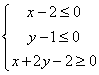
表示的平面区域上运动，则
的取值范围是
( )
A．
B．
C．
D．
５．若圆x2 +y2－4x－4y－10=0上至少有三个不同的点到直线l:ax+by=0的距离为2,则直线
的倾斜角的取值范围是 （ ）
A．[，] B．[，] C．[，] D．[0，]
６．不等式≤a≤在t∈(0，2]上恒成立，则a的取值范围是 ( )
A．[，1] B．[，1] C．[，] D．[，2]
7．在锐角△ABC中，若tanA＝t＋1，tanB＝t－1，则t的取值范围是 ( )
A．(,＋∞) B．(1,＋∞) C．(1, ) D．(－1,1)
8．若半径为R的球与正三棱柱的各个面都相切，则球与正三棱柱的体积比为( )
A．π B．π C．π D．π
9．曲线
在区间
上截直线
与
所得的弦长相等且不为0，则下列对
的描述正确的是
（ ）
A．
B．
C．
D．
10．已知不等式
,若对任意
及
该不等式恒成立，
则实数
的取值范围是
( )
（A）
（B）
（C）
（D）
二、填空题（5*6=30分）
11. 若
(n∈N)的展开式中第3项为常数项，则展开式中二项式系数最大的是第____________项．
12. 在平面直角坐标系中,点A在圆
上,点B在直线
上,则线段AB的最小值=
13. 5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种 (以数作答)。
14. 将函数y＝x2的图象F按向量＝(3,－2)平移到F′，则F′的函数解析式为＿＿＿＿．
15. 已知函数
的值为_______________
16. 设函数
在区间
上的最大值为8，则
在区间
上的最小值为________________.
三、解答题：（70分）
17．(本大题满分12分）
在锐角三角形ABC中，已知内角A、B、C所对的边分别为a、b、c，且
（成都）
（I）若
，求A、B、C的大小；
（II）已知向量
的取值范围.
18．(本大题满分14分）
据调查，某地区100万从事传统农业的农民，人均收入3000元，为了增加农民的收入，当地政府积极引进资本，建立各种加工企业，对当地的农产品进行深加工，同时吸收当地部分农民进入加工企业工作，据估计，如果有x(x＞0)万人进企业工作，那么剩下从事传统农业的农民的人均收入有望提高2x%，而进入企业工作的农民的人均收入为3000a元（a＞0）。
（1）在建立加工企业后，要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入，试求x的取值范围；
（2）在（1）的条件下，当地政府应该如何引导农民（即x多大时），能使这100万农民的人均年收入达到最大。
19．（本小题满分14分）在三棱锥
中，△ABC是边长为4的正三角形，平面
，
，M、N分别为AB、SB的中点。
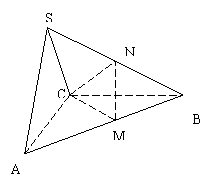（1）证明：
；
（2）求二面角N－CM－B的大小；
（3）求点B到平面CMN的距离。
20．(本大题满分14分）
函数
的最小值为
且
数列
的前
项和为
．
（Ⅰ）求数列
的通项公式；
（Ⅱ）若数列
是等差数列，且
，求非零常数
；
（Ⅲ）若
，求数列
的最大项．
21．(本大题满分16分）
(1) 已知抛物线
过焦点
的动直线l交抛物线于
两点, 
为坐标原点, 求证: 
为定值;
(2) 由 (1) 可知: 过抛物线的焦点的动直线 l 交抛物线于两点, 存在定点
, 使得
为定值. 请写出关于椭圆的类似结论,并给出证明.
双周考测试卷参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | C | C | B | B | A | B | A | C |
二、 填空题
11. 5 12. 15 13. 48种 14. y＝x2－6x＋7 15. 
16. -4
三、解答题
17.【解】解：由已知
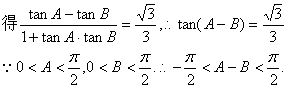
…………………………………………………………3分
（I）由已知
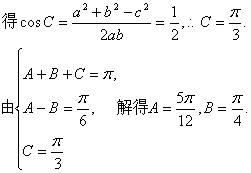
……………………………………………………3分
（II）3m－2n2=9 m 2+4n2－12 m·n =13－12（sinAcos B +cosAsin B）
=13－12sin(A+B)=13－12sin（2 B +
）.………………………3分
∵△ABC为锐角三角形，A－B=，
∴C=π－A－B<
，A=+B<.
…………………………………………………………2分
∴3m－2n2=∈（1，7）.
∴3m－2n的取值范围是（1，
）.…………………………………………1分
18.【解】（1）由题意得（100-x）·3000·（1+2x%）≥100×3000，
即x2－50x≤0，解得0≤x≤50， ……………………4分
又∵x＞0 ∴0＜x≤50； ……………………6分
（2）设这100万农民的人均年收入为y元，
则y=
=
=－[x－25(a+1)]2+3000+475(a+1)2 (0≤x≤50) ………………10分
i当25(a+1)≤50，即0＜a≤1，当x=25(a+1)时，y最大； ………………12分
ii当25(a+1)＞50，即a ＞1，函数y在（0,50]单调递增，
∴当x=50时，y取最大值。
答：在0＜a≤1时，安排25(a +1)万人进入企业工作，在a＞1时安排50万人进入企业工作，才能使这100万人人均年收入最大。 ………………16分
19
|
|
解：（1）取AC中点P，由
知：
|
|
|
|
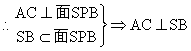
（2）由（1）知：，又平面，
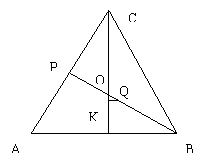取BP中点Q，连结NQ
又N为SB中点
，而
，
过Q作
，连结NK，
则
即为二面角N－CM－B的平面角
设CM交BP于O，则
，
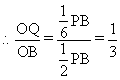
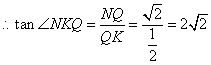
所以二面角N－CM－B的大小为
。
（3）由（2）知：
设B到平面CMN的距离为d，则
， 
点B到平面CMN的距离为
。
20．解：（Ⅰ）由
，
，
由题意知：
的两根，
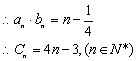
（Ⅱ）
，
为等差数列，
，
，
经检验
时，是等差数列，
（Ⅲ）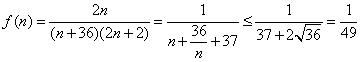
21．解: (1) 若直线l垂直于x轴, 则
, 
.
……………2分
若直线l不垂直于轴, 设其方程为
, 
.
由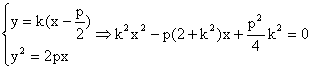
……………4分
.
综上, 
为定值. ……………6分
(2) 关于椭圆有类似的结论: 过椭圆
的一个焦点的动直线l交椭圆于
、
两点, 存在定点, 使为定值. ……………7分
证明: 不妨设直线l过椭圆
的右焦点
其中
若直线l不垂直于轴, 则设其方程为: 
, .
由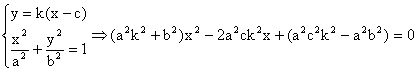
得:
所以
……………9分
由对称性可知, 设点在x轴上, 其坐标为
所以
要使为定值,
只要
即
此时
……………12分
若直线l垂直于x轴, 则其方程为
, 
, 
.
取点
有
……………13分
综上, 过焦点
的任意直线l交椭圆于、两点, 存在定点
使
为定值. ……………14分