2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(7)—圆锥曲线
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若椭圆经过原点,且焦点为![]() ,则其离心率为 ( )
,则其离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知双曲线![]() ,则双曲线右支上的点P到右焦点的距离与点P到右准线的距离
,则双曲线右支上的点P到右焦点的距离与点P到右准线的距离
之比等于 ( )
A.![]() B.
B.![]() C. 2 D.4
C. 2 D.4
4.与![]() 轴相切且和半圆
轴相切且和半圆![]() 内切的动圆圆心的轨迹方程是 ( )
内切的动圆圆心的轨迹方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
5.直线![]() 与曲线
与曲线![]()
![]() 的公共点的个数为 ( )
的公共点的个数为 ( )
A. 1 B. 2 C. 3 D. 4
6.如果方程![]() 表示曲线,则下列椭圆中与该双曲线共焦点的是 ( )
表示曲线,则下列椭圆中与该双曲线共焦点的是 ( )
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
7.曲线![]() 与曲线
与曲线![]() 的 ( )
的 ( )
A.焦距相等 B.离心率相等 C.焦点相同 D.准线相同
8.双曲线![]() 的虚轴长是实轴长的2倍,则
的虚轴长是实轴长的2倍,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.设过点![]() 的直线分别与
的直线分别与![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴交于
轴的正半轴交于![]() 、
、![]() 两点,点
两点,点![]() 与点
与点![]()
关于![]() 轴对称,
轴对称,![]() 为坐标原点,若
为坐标原点,若![]() ,且
,且![]() ,则
,则![]() 点的轨迹方程是 ( )
点的轨迹方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.抛物线![]() 上的点到直线
上的点到直线![]() 距离的最小值是 ( )
距离的最小值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知抛物线![]() 上一定点
上一定点![]() 和两动点
和两动点![]() 当
当![]() 是,点
是,点![]() 的横坐标的取值范围是 ( )
的横坐标的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
![]()
![]()
12.椭圆![]() 上有
上有![]() 个不同的点:
个不同的点:![]() ,椭圆的右焦点为
,椭圆的右焦点为![]() ,数列
,数列![]() 是公差大于
是公差大于![]() 的等差数列,则
的等差数列,则![]() 的最大值为 ( )
的最大值为 ( )
A.199 B.200 C.198 D.201
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中的横线上)
 13.椭圆
13.椭圆![]() 的两个焦点为
的两个焦点为![]() ,点
,点![]() 在椭圆上.如果线段
在椭圆上.如果线段![]() 的中点在
的中点在![]() 轴上,那么
轴上,那么![]() 是
是![]() 的______________倍.
的______________倍.
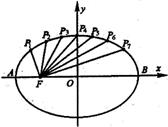
14.如图把椭圆![]() 的长轴AB分成8等
的长轴AB分成8等
分,过每个分点作x轴的垂线交椭圆的上半部
分于P1,P2,…,P7七个点,F是椭圆的焦点,则P1F+P2F+…+P7F= .
15.要建造一座跨度为16米,拱高为4米的抛物线拱桥,建桥时,每隔4米用一根柱支撑,两边的柱长应为____________.
16.已知两点![]() ,给出下列直线方程:①
,给出下列直线方程:①![]() ;②
;②![]() ;③
;③![]() .则在直线上存在点
.则在直线上存在点![]() 满足
满足![]() 的所有直线方程是_______.(只填序号)
的所有直线方程是_______.(只填序号)
三、解答题(本大题共6小题, 共74分,解答应写出文字说明,证明过程或演算步骤)
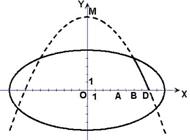 17.(本小题满分12分)学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为
17.(本小题满分12分)学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() . 观测点
. 观测点![]() 同时跟踪航天器.
同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]()
测得离航天器的距离分别为多少时,应向航天
器发出变轨指令?
18.(本小题满分12分)已知三点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0)。
(6,0)。
(1)求以![]() 、
、![]() 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(2)设点P、![]() 、
、![]() 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为![]() 、
、![]() 、
、![]() ,求以
,求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程.
的双曲线的标准方程.
19.(本小题满分12分)已知椭圆的中心在原点,离心率为![]() ,一个焦点是
,一个焦点是![]() (
(![]() 为大于0的常数).
为大于0的常数).
(1)求椭圆的方程;
(2)设![]() 是椭圆上一点,且过点
是椭圆上一点,且过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
20.(本小题满分12分)已知点![]() 分别是椭圆
分别是椭圆![]() 长轴的左、右端点,点
长轴的左、右端点,点![]() 是椭圆的右焦点.点
是椭圆的右焦点.点![]() 在椭圆上,且位于
在椭圆上,且位于![]() 轴的上方,
轴的上方,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)设![]() 椭圆长轴
椭圆长轴![]() 上的一点,
上的一点, ![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,求椭圆上的点到点
,求椭圆上的点到点![]() 的距离
的距离![]() 的最小值.
的最小值.
21.(本小题满分12分)已知抛物线![]() ,是否存在过点
,是否存在过点![]() 的弦
的弦![]() ,使
,使![]() 恰被
恰被![]() 平分.若存在,请求
平分.若存在,请求![]() 所在直线的方程;若不存在,请说明理由.
所在直线的方程;若不存在,请说明理由.
22.(本小题满分14分)设![]() ,
,![]() 为直角坐标平面内
为直角坐标平面内![]() 轴正方向上的单位向量,若向量
轴正方向上的单位向量,若向量![]() ,
,![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点(0,3)作直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,设
两点,设![]() ,是否存在这样的直线
,是否存在这样的直线![]() ,使得四边形
,使得四边形![]() 是矩形?若存在,求出直线
是矩形?若存在,求出直线![]() 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
答案与解析(7)
1.C
. 原点到![]() 的距离之和是长轴长
的距离之和是长轴长![]() ,又
,又![]() ,所以椭圆的离心率
,所以椭圆的离心率![]() .
.
2.D
. 椭圆![]() 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线![]() 的焦点为(2,0),则
的焦点为(2,0),则![]() ,故选D.
,故选D.
3.答案选C 依题意可知 ![]() ,
,
![]() ,故选C.
,故选C.
4.A
设动圆圆心为![]() ,动圆与已知半圆相切的切点为
,动圆与已知半圆相切的切点为![]() ,点
,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,则有
,则有![]() ,而
,而![]() ,所以
,所以![]() ,化简得
,化简得![]() .
.
5.D.将![]() 代入
代入![]() 得:
得:![]()
![]() ,显然该关于
,显然该关于![]() 的方程有两正解,即x有四解,所以交点有4 个,故选择答案D.
的方程有两正解,即x有四解,所以交点有4 个,故选择答案D.
6.D.由题意知,![]() .若
.若![]() ,则双曲线的焦点在
,则双曲线的焦点在![]() 轴上,而在选择支A,C中,椭圆的焦点都在
轴上,而在选择支A,C中,椭圆的焦点都在![]() 轴上,而选择支B,D不表示椭圆;
轴上,而选择支B,D不表示椭圆;
若![]() ,选择支A,C不表示椭圆,双曲线的半焦距平方
,选择支A,C不表示椭圆,双曲线的半焦距平方![]() ,双曲线的焦点在
,双曲线的焦点在![]() 轴上,选择支D的方程符合题意.
轴上,选择支D的方程符合题意.
7.A.由![]() 知该方程表示焦点在x轴上的椭圆,由
知该方程表示焦点在x轴上的椭圆,由![]() 知该方程表示焦点在y轴上的双曲线,故只能选择答案A.
知该方程表示焦点在y轴上的双曲线,故只能选择答案A.
8.A . 一看带参,马上戒备:有没有说哪个轴是实轴?没说,至少没有明说。分析一下,因为等号后为常数“+”,所以等号前为系数为“+”的对应实轴。y2的系数为“+”,所以这个双曲线是“立”着的。接下来排除C、D两过于扯淡的选项 —— 既然说是双曲线,“x2”与“y2”的系数的符号就不能相同.在接下来是一个“坑儿”:双曲线的标准形式是![]() 或
或![]() (
(![]() ),题目中的双曲线方程并不是标准形式,所以要变一下形儿,变成
),题目中的双曲线方程并不是标准形式,所以要变一下形儿,变成![]() 。由题意,半虚轴长的平方:半实轴长的平方 = 4.即
。由题意,半虚轴长的平方:半实轴长的平方 = 4.即![]() ,所以
,所以![]() 。选A.当然,我们也可以不算,只利用半虚轴比半实轴长即可直接把答案A圈出来
。选A.当然,我们也可以不算,只利用半虚轴比半实轴长即可直接把答案A圈出来
9.D.由![]() 及
及![]() 分别在
分别在![]() 轴的正半轴和
轴的正半轴和![]() 轴的正半轴上知,
轴的正半轴上知,![]()
![]() ,
,![]() ,由点
,由点![]() 与点
与点![]() 关于
关于![]() 轴对称知,
轴对称知,![]() ,
,![]() =
=![]() ,则
,则![]()
10.A
.抛物线上任意一点(![]() ,
,![]() )到直线的距离
)到直线的距离![]() .因为
.因为![]() ,所以
,所以![]() 恒成立.从而有
恒成立.从而有![]() ,
,![]() .选A.
.选A.
11.D
.由题意知,设![]() ,又因为
,又因为![]() ,由
,由![]() 知,
知,![]() ,即
,即![]() ,也就是
,也就是![]() ,因为
,因为![]() ,所以上式化简得
,所以上式化简得![]() ,由基本不等式可得
,由基本不等式可得![]() 或
或![]() .
.
12.D
. 由题意知,要使所求的![]() 最大,应使
最大,应使![]() 最小,
最小,![]() 最大,又
最大,又![]() 为椭圆的右焦点,设
为椭圆的右焦点,设![]() 的横坐标为
的横坐标为![]() 故由第二定义可得,
故由第二定义可得,![]() ,其中
,其中![]() ,所以当
,所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() 最大.由等差数列的通项公式可得,
最大.由等差数列的通项公式可得, ![]() ,即
,即![]() ,又因为
,又因为![]() ,解得
,解得![]() .
.
13.7倍.
由已知椭圆的方程得![]() .由于焦点
.由于焦点![]()
关于![]() 轴对称,所以
轴对称,所以![]() 必垂直于
必垂直于![]() 轴.所以
轴.所以
![]() ,所以
,所以![]() .
.
14.35. 设P1(x1,y1),P2(x2,y2),…,P7(x7,y7),所以根据对称关系x1+x2+…+x7=0,于是
P1F+P2F+…+P7F=a+ex1+a+ex2+…+a+ex7=7a+e(x1+x2+…+x7)= 7a=35,所以应填35.
15.1米. 由题意知,设抛物线的方程为![]() ,又抛物线的跨度为16,拱高为4,所以点(8,-4)为抛物线上的点,所以
,又抛物线的跨度为16,拱高为4,所以点(8,-4)为抛物线上的点,所以![]() .即抛物线方程为
.即抛物线方程为![]() .所以当
.所以当![]() 时,
时,![]() ,所以柱子的高度为1米.
,所以柱子的高度为1米.
16.②③. 由![]() 可知点
可知点![]() 在双曲线
在双曲线![]() 的右支上,故只要判断直线与双曲线右支的交点个数.因为双曲线的渐近线方程为
的右支上,故只要判断直线与双曲线右支的交点个数.因为双曲线的渐近线方程为![]() ,直线①过原点且斜率
,直线①过原点且斜率![]() ,所以直线①与双曲线无交点;直线②与直线①平行,且在
,所以直线①与双曲线无交点;直线②与直线①平行,且在![]() 轴上的截距为
轴上的截距为![]() 故与双曲线的右支有两个交点;直线③的斜率
故与双曲线的右支有两个交点;直线③的斜率![]() ,故与双曲线的右支有一个交点.
,故与双曲线的右支有一个交点.
17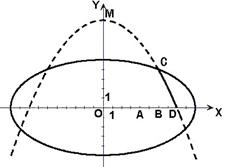 .(1)设曲线方程为
.(1)设曲线方程为![]() ,
,
由题意可知,![]() .
.
![]() .
.
![]() 曲线方程为
曲线方程为![]() .
.
(2)设变轨点为![]() ,根据题意可知
,根据题意可知
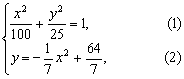 得
得 ![]() ,
,
![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去). ![]() .
.
得 ![]() 或
或![]() (不合题意,舍去).
(不合题意,舍去). ![]()
![]() 点的坐标为
点的坐标为![]() ,
,
![]() .
.
答:当观测点![]() 测得
测得![]() 距离分别为
距离分别为![]() 时,应向航天器发出变轨指令.
时,应向航天器发出变轨指令.
18.(1)由题意,可设所求椭圆的标准方程为![]() +
+![]()
![]() ,其半焦距
,其半焦距![]() 。
。
![]()
![]() , ∴
, ∴![]()
![]() ,
,
![]() ,故所求椭圆的标准方程为
,故所求椭圆的标准方程为![]() +
+![]() ;
;
(2)点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0)关于直线y=x的对称点分别为:
(6,0)关于直线y=x的对称点分别为:
![]() 、
、![]() (0,-6)、
(0,-6)、![]() (0,6)
(0,6)
设所求双曲线的标准方程为![]() -
-![]()
![]() ,由题意知半焦距
,由题意知半焦距![]() ,
,
![]()
![]() , ∴
, ∴![]()
![]() ,
,
![]() ,故所求双曲线的标准方程为
,故所求双曲线的标准方程为![]() -
-![]() .
.
19.(1)设所求椭圆方程为:![]() .由已知得:
.由已知得:![]() ,所以
,所以![]() .故所求椭圆的方程为:
.故所求椭圆的方程为:![]() .
.
(2)设![]() ,直线
,直线![]() ,则点
,则点![]() .当
.当![]() 时,由于
时,由于![]() .由定比分点坐标公式,得
.由定比分点坐标公式,得![]() ,
,![]() .又点
.又点![]() 在椭圆上,所以
在椭圆上,所以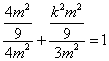 ,解得
,解得![]() .当
.当![]() 时,
时,![]() ,
,![]() .于是
.于是![]() ,解得
,解得![]() .故直线
.故直线![]() 的斜率为0或
的斜率为0或![]() .
.
20.(1)由已知可得点![]() , 设点
, 设点![]() ,则
,则![]() ,
,![]() ,由已知可得
,由已知可得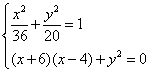 .则
.则![]() 解得
解得![]() .由于
.由于![]() ,只能
,只能![]() 于是
于是![]() . 所以点P的坐标是
. 所以点P的坐标是![]() .
.
(2)直线![]() 的方程是
的方程是![]() .设点
.设点![]() ,则
,则![]() 到直线
到直线![]() 的距离是
的距离是![]() . 于是
. 于是![]() ,又
,又![]() ,解得
,解得![]() . 椭圆上的点
. 椭圆上的点![]() 到点
到点![]() 的距离
的距离![]() 有
有![]()
![]() ,由于
,由于![]() ,所以当
,所以当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
21.假设存在这样的直线,则直线的斜率一定存在,设为![]() ,点
,点![]() 在抛物线上,所以
在抛物线上,所以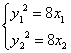 ,两式作差得,
,两式作差得,![]() ,即
,即![]() ,解得
,解得![]() ,故直线方程为
,故直线方程为![]() ,即
,即![]() .经验证,直线符合条件.
.经验证,直线符合条件.
22.(1)由![]() ,得
,得![]() ,设
,设![]() 则动点
则动点![]() 满足
满足![]() ,所以点
,所以点![]() 在椭圆上,且椭圆的
在椭圆上,且椭圆的![]() .所以轨迹
.所以轨迹![]() 的方程为
的方程为![]() .
.
(2)设直线的斜率为![]() ,则直线方程为
,则直线方程为![]() ,联立方程组
,联立方程组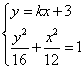 消去
消去![]() 得:
得:![]() ,
,![]() 恒成立,设
恒成立,设![]() ,则
,则![]() .由
.由![]() ,所以四边形
,所以四边形![]() 为平行四边形.若存在直线
为平行四边形.若存在直线![]() ,使四边形
,使四边形![]() 为矩形,则
为矩形,则![]() ,即
,即![]() ,解得
,解得![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,此时四边形
,此时四边形![]() 为矩形.
为矩形.
欢迎访问 http://www.k12zy.com