高三数学复习卷(周末卷)2007.3
班级_______姓名_____________学号_____得分______
一、填空题 (本大题共12小题,每小题4分,共48分)
1.已知函数![]() ,则方程
,则方程![]() 的解
的解![]() ___1___.
___1___.
2. 已知集合![]() ,集合
,集合![]() ,则
,则![]() =
= ![]()
3. 设A、B、C是三个集合,则“A∩B=A∩C”是“B=C”的 必要非充分 条件。
4. 已知f (x)=x5+ax3+bx-8,且f (-2)=10,那么f (2)= -26 。
5. 设函数 f(x)在 (-∞,+∞)内有定义,下列函数
(1) y=-f(x); (2) y= x f(x2); (3) y=-f(-x); (4) y=f(x)-f(-x)
中必为奇函数的有▁▁▁⑵⑷▁▁▁(要求填写正确答案的序号)。
6.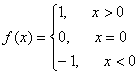 ,则方程
,则方程![]() 的各个解之和为
的各个解之和为
![]()
7.已知函数y=f (x)是奇函数,周期T=5,若f(-2)=2a-1则f (7)= 1-2a
8若复数z=sin2![]() 1+
1+![]() 为纯虚数,则角θ组成的集合为___________。
为纯虚数,则角θ组成的集合为___________。![]() 。
。
9.某班有50名学生,其中 15人选修A课程,另外35人选修B课程.从班级中任选两名学生,他们是选修不同课程的学生的概率是 ![]() (结果用分数表示).
(结果用分数表示).
10.7.把下面不完整的命题补充完整,并使之成为真命题:若函数![]() 的图象
的图象
与![]() 的图象关于 对称,则函数
的图象关于 对称,则函数![]() = .
= .
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
(①x轴,![]() ②y轴,
②y轴,![]() )③原点,
)③原点,![]() ④直线
④直线![]()
11. 已知集合M={x1≤x≤10,x∈N},对它的非空子集A,将A中每个元素k,都乘以(-1)k再求和(如A={1,3,6},可求得和为(-1)·1+(-1)3·3+(-1)6·6=2,则对M的所有非空子集,这些和的总和是 2560 .
12. 已知![]() 次多项式
次多项式![]() ,如果在一种计算中,计算
,如果在一种计算中,计算![]() 的值需要
的值需要![]() 次乘法。计算
次乘法。计算![]() 的值共需要
的值共需要![]() 次运算(
次运算(![]() 次乘法,
次乘法,![]() 次加法),那么计算
次加法),那么计算![]() 的值共需要_
的值共需要_![]() __________次运算。下面给出一种减少运算次数的算法:
__________次运算。下面给出一种减少运算次数的算法:![]() ,利用该算法,计算
,利用该算法,计算![]() 的值共需要
的值共需要![]() 次运算,计算
次运算,计算![]() 的值共需要 _2n _____次运算。
的值共需要 _2n _____次运算。
二、选择题(本大题共4小题,共16分)
13.若函数y=f (x) (f (x)不恒为零)的图象与函数y=-f (x)的图象关于原点对称,则函数y=f (x)
(A)是奇函数而不是偶函数 (B)是偶函数而不是奇函数
(C)既是奇函数又是偶函数 (D)既不是奇函数又不是偶函数设函数 ( B )
14.三人互相传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍然回到甲手中,则不同的传球方式有( C )(A)6种 B) 8种(C) 10种(D)16种
15、已知关于x的方程:2x=x2解的个数为 ( C )
(A)1 (B)2 (C)3 (D) 4
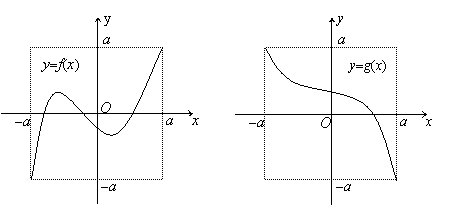
16.定义域和值域均为[-a,a] (常数a>0)的函数y=f(x)和y=g(x)的图像如图所示,
给出下列四个命题中:
(1) 方程f[g(x)]=0有且仅有三个解; (2) 方程g[f(x)]=0有且仅有三个解;
(3) 方程f[f(x)]=0有且仅有九个解; (4)方程g[g(x)]=0有且仅有一个解。
那么,其中正确命题的个数是 ( B )
(A) 1; (B) 2; (C) 3; (D) 4。
三、解答题(本大题共6小题,共86分,解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分12分)
设函数![]() ,其中
,其中![]() (1)解不等式
(1)解不等式![]() (2)求
(2)求![]() 的取值范围,使
的取值范围,使![]() 在区间
在区间![]() 上是单调减函数。
上是单调减函数。
解:(1)不等式![]() 即为
即为![]()
当![]() 时,不等式解集为
时,不等式解集为![]()
当![]() 时,不等式解集为
时,不等式解集为![]()
当![]() 时,不等式解集为
时,不等式解集为![]()
(2)在![]() 上任取
上任取![]() ,则
,则![]()
![]()
所以要使![]() 在
在![]() 递减即
递减即![]() ,
,
只要![]() 即
即![]()
故当![]() 时,
时,![]() 在区间
在区间![]() 上是单调减函数。
上是单调减函数。
18. (本小题满分12分)
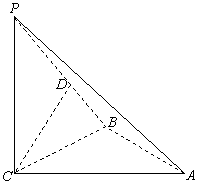 如图,三棱锥
如图,三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() 平面
平面![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的大小;600
所成角的大小;600
(作矩形ABCE则![]() PAE为所求)
PAE为所求)
(3)求二面角![]() 的大小(结果用反三角函数值表示).
的大小(结果用反三角函数值表示).
![]()
19. (本小题满分14分)袋内装有![]() 个球,每个球上都记有从
个球,每个球上都记有从![]() 到
到![]() 的一个号码,设号码
的一个号码,设号码![]() 的球重
的球重![]() 克,这些球以等可能性从袋里取出(不受重量、号码的影响)。
克,这些球以等可能性从袋里取出(不受重量、号码的影响)。
(1)如果任意取出![]() 球,试求其重量数(克)大于号码数加
球,试求其重量数(克)大于号码数加![]() 的概率;
的概率;
(2)如果任意取出![]() 球,试求它们重量相等的概率。
球,试求它们重量相等的概率。
解:(1)由![]()
![]() 得
得![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() 共有
共有![]() 个不同的值,∴所求概率
个不同的值,∴所求概率![]() 。
。
(2)∵![]()
![]() ,
,
∴![]() 时分别与
时分别与![]() 时的值相等,∴所求概率
时的值相等,∴所求概率![]() 。
。
20. (本小题满分14分) 设函数![]() ,函数
,函数![]() ,其中
,其中![]() 为常数且
为常数且![]() ,令函数
,令函数![]() 为函数
为函数![]() 和
和![]() 的积函数。(1)求函数
的积函数。(1)求函数![]() 的表达式,并求其定义域;(2)当
的表达式,并求其定义域;(2)当![]() 时,求函数
时,求函数![]() 的值域;(3)是否存在自然数
的值域;(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰为
的值域恰为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由。
所构成的集合;若不存在,试说明理由。
解:(1)![]() ,
,![]() 。
。
(2)∵![]() ,∴函数
,∴函数![]() 的定义域为
的定义域为![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
∴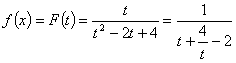 ,
,
∵![]() 时,
时,![]() ,又
,又![]() 时,
时,![]() 递减,∴
递减,∴![]() 单调递增,
单调递增,
∴![]() ,即函数
,即函数![]() 的值域为
的值域为![]() 。
。
(3)假设存在这样的自然数![]() 满足条件,令
满足条件,令![]() ,则
,则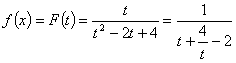 ,
,
∵![]() ,则
,则![]() ,要满足值域为
,要满足值域为![]() ,则要满足
,则要满足![]() ,
,
由于当且仅当![]()
![]() 时,有
时,有![]() 中的等号成立,且此时
中的等号成立,且此时![]() 恰为最大值,
恰为最大值,
∴![]() ,
,
又![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,∴
上是减函数,∴![]()
![]() ,
,
综上,得 ![]() 。
。
21.(本小题满分16分) 设f(k)是满足不等式log2x+log2(3·2k-1-x)≥2K-1,(k![]() 的自然数x的个数,
的自然数x的个数,
(1)求f(k)的解析式;
(2)记Sn=f(1)+f(2)+……+f(n),求Sn解析式;
(3)记Pn=n-1,设Tn=![]() ,对任意n
,对任意n![]() 均有Tn<m成立,
均有Tn<m成立,
求出整数m的最小值。
解:(1)原不等式ó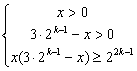 ó
ó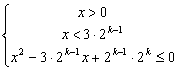
ó![]() (4分)Þ
(4分)Þ![]() .
.
(2)![]() .
.
(3)![]() ,
,
当1≤n≤9时,![]() ¯,此时
¯,此时![]() ,
,
当n≥10时,![]() ¯,此时
¯,此时![]() ,
,
∴![]() ,
,![]() .
.
22.(本小题满分18分)
已知函数![]() 的最大值为正实数,集合
的最大值为正实数,集合
![]() ,集合
,集合![]() 。
。
(1)求![]() 和
和![]() ;
;
(2)定义![]() 与
与![]() 的差集:
的差集:![]() 且
且![]() 。
。
设![]() ,
,![]() ,
,![]() 均为整数,且
均为整数,且![]() 。
。![]() 为
为![]() 取自
取自![]() 的概率,
的概率,![]() 为
为![]() 取自
取自![]() 的概率,写出
的概率,写出![]() 与
与![]() 的二组值,使
的二组值,使![]() ,
,![]() 。
。
(3)若函数![]() 中,
中,![]() ,
,![]() 是(2)中
是(2)中![]() ,b最大的一组,试写出
,b最大的一组,试写出![]() 在区间[
在区间[![]() ,n]上的最大值函数
,n]上的最大值函数![]() 的表达式。
的表达式。
22. (1)∵![]() ,配方得
,配方得![]() ,
,
由![]() 得最大值
得最大值![]() 。
。
∴![]() ,
,![]() 。
。
(2)要使![]() ,
,![]() 。可以使①
。可以使①![]() 中有3个元素,
中有3个元素,![]() 中有2个元素,
中有2个元素,
![]() 中有1个元素。则
中有1个元素。则![]() 。
。
②![]() 中有6个元素,
中有6个元素,![]() 中有4个元素,
中有4个元素, ![]() 中有2个元素。则
中有2个元素。则![]()
(3)由(2)知![]()
![]()
![]()