2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(4)—《平面向量》
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
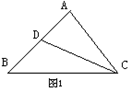 1.如图1所示,D是△ABC的边AB上的中点,
1.如图1所示,D是△ABC的边AB上的中点,
则向量![]() (
)
(
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.与向量a=![]()
![]() 的夹解相等,且模为1的向量是 ( )
的夹解相等,且模为1的向量是 ( )
A.![]() B.
B.![]() 或
或![]()
C.![]() D.
D.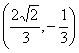 或
或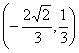
3.设![]() 与
与![]() 是两个不共线向量,且向量
是两个不共线向量,且向量![]() 与
与![]() 共线,则
共线,则![]() = ( )
= ( )
A.0 B.-1 C.-2 D.0.5
4.已知向量![]() ,
,![]() 是不平行于
是不平行于![]() 轴的单位向量,且
轴的单位向量,且![]() ,则
,则![]() = ( )
= ( )
A.![]() B.
B.![]() C.
C.![]() D.(1,0)
D.(1,0)
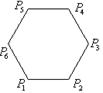 5.如图,已知正六边形P1P2P3P4P5P6,下列向量
5.如图,已知正六边形P1P2P3P4P5P6,下列向量
的数量积中最大的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上的高,若
边上的高,若![]() ,则实数
,则实数![]() 等
等
于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设![]() ,
,![]() ,则满足条件
,则满足条件![]() ,
,![]() 的动点P的
的动点P的
变化范围(图中阴影部分含边界)是 ( )
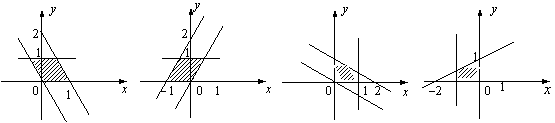 |
A. B. C. D.
8.将函数f(x)=tan(2x+![]() )+1按向量a平移得到奇函数g(x),要使a最小,则a=( )
)+1按向量a平移得到奇函数g(x),要使a最小,则a=( )
A.(![]() ) B.(
) B.(![]() ) C.(
) C.(![]() ) D.(
) D.(![]() )
)
9.已知向量![]() 、
、![]() 、
、![]() 且
且![]() ,
,![]() ,
,![]() ,
,![]() .设
.设![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]()
与![]() 的夹角为
的夹角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,则它们的大小关系是 ( )
,则它们的大小关系是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知向量![]() ,
,![]() ,其中
,其中![]() .若
.若![]() ,则当
,则当![]() 恒成立时实数
恒成立时实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]()
11.已知![]() ,
,![]() ,
,![]() ,点C在
,点C在![]() 内,且
内,且![]() ,设
,设![]()
![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
12.对于直角坐标平面内的任意两点![]() ,
,![]() ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”:![]() 给出下列三个命题:
给出下列三个命题:
①若点C在线段AB上,则![]()
②在![]() 中,若
中,若![]() 则
则![]()
③在![]() 中,
中,![]()
其中真命题的个数为 ( )
A.0 B.1 C.2 D.3
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
![]() 13.在 ABCD中,
13.在 ABCD中,![]() ,M为BC的中点,则
,M为BC的中点,则![]() _______.(用
_______.(用![]() 表示)
表示)
14.已知![]() 为坐标原点,动点
为坐标原点,动点![]() 满足
满足![]() ,其中
,其中![]() 且
且![]() ,则
,则![]() 的轨迹方程为
.
的轨迹方程为
.
15.在ΔABC中,O为中线AM上的一个动点,若AM=2,则![]() 的最小值为
的最小值为
.
16.已知向量![]() ,若点A、B、C能构成三角形,则实数m满足的条件是 .
,若点A、B、C能构成三角形,则实数m满足的条件是 .
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知向量![]() ,
,![]() .(1)若
.(1)若![]() ,试判断
,试判断![]() 与
与![]() 能否平行?(2)若
能否平行?(2)若![]() ,求函数
,求函数![]() 的最小值.
的最小值.
18.(本小题满分12分)(2006年湖北卷)设函数![]() ,其中向量
,其中向量
![]() ,
,![]() .
.
(1)求函数![]() 的最大值和最小正周期;
的最大值和最小正周期;
(2)将函数![]() 的图像按向量
的图像按向量![]() 平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的
平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的![]() .
.
19.(本小题满分12分)(2006年全国卷II)已知向量a=(sinθ,1),b=(1,cosθ),
-<θ<.
(1)若a⊥b,求θ;
(2)求|a+b|的最大值.
20.(本小题满分12分)在![]() 中,
中,![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 的面积最大时,求
的面积最大时,求![]() 的大小.
的大小.
21.(本小题满分12分)(2006陕西卷)如图,三定点A(2,1),B(0,-1),C(-2,1); 三动点D,E,M满足![]()
(1)求动直线DE斜率的变化范围;
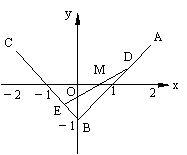 (2)求动点M的轨迹方程.
(2)求动点M的轨迹方程.
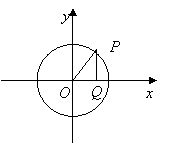
22.(本小题满分14分)已知点![]() 是圆
是圆![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,设
,设![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)求向量![]() 和
和![]() 夹角的最大值,并求此时
夹角的最大值,并求此时![]() 点的坐标
点的坐标
 |
参考答案(4)
1.![]() ,故选A.
,故选A.
2.B 设所求向量![]() =(cos
=(cos![]() ,sin
,sin![]() ),则由于该向量与
),则由于该向量与![]() 的夹角都相等,故
的夹角都相等,故
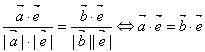
![]()
![]() 3cos
3cos![]() =-4sin
=-4sin![]() ,为减少计算量,可将选项代入验证,可知B选项成立,故选B.
,为减少计算量,可将选项代入验证,可知B选项成立,故选B.
3.D 依题意知向量![]() 与
与![]() 共线,设
共线,设![]()
![]() (
(![]() ),则有
),则有![]() ,所以
,所以![]() ,解得
,解得![]() ,选D.
,选D.
4.解选B.设![]() ,则依题意有
,则依题意有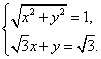
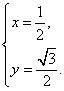
5.解析:利用向量数量积![]() 的几何意义:数量积
的几何意义:数量积![]() 等于
等于![]() 的长度
的长度![]() 与
与![]() 在
在![]() 的方向上的投影
的方向上的投影![]() 的乘积.显然由图可知
的乘积.显然由图可知![]() 在
在![]() 方向上的投影最大.所以应选(A).
方向上的投影最大.所以应选(A).
6.B ![]() 即得
即得![]() 又
又![]() 是
是![]() 边上的高,
边上的高,![]() 即
即![]() ,整理可得
,整理可得![]() 即得
即得![]() ,故选B.
,故选B.
7.A 设P点坐标为![]() ,则
,则![]() .由
.由![]() ,
,![]() 得
得![]() ,在平面直角坐标系中画出该二元一次不等式组表示的平面区域即可,选A.
,在平面直角坐标系中画出该二元一次不等式组表示的平面区域即可,选A.
8.A 要经过平移得到奇函数g(x),应将函数f(x)=tan(2x+![]() )+1的图象向下平移1个单位,再向右平移
)+1的图象向下平移1个单位,再向右平移![]() 个单位.即应按照向量
个单位.即应按照向量![]() 进行平移.要使a最小,应取a=(
进行平移.要使a最小,应取a=(![]() ),故选A.
),故选A.
9.B 由![]() 得
得![]() ,两边平方得
,两边平方得![]() ,将
,将![]() ,
,![]() ,
,![]() 代入得
代入得![]() ,所以
,所以![]() ;同理,由
;同理,由![]() 得
得![]() ,可得
,可得![]() ,
,![]() ,所以
,所以![]() .
.
10. B 由已知得![]() ,所以
,所以![]() ,因此
,因此![]()
![]() ,由于
,由于![]() 恒成立,所以
恒成立,所以![]() ,解得
,解得![]() 或
或![]() .
.
11.答案B∵ ![]() ,
,![]() ,
,![]()
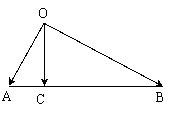 ∴△ABC为直角三角形,其中
∴△ABC为直角三角形,其中![]()
∴![]()
∴![]() 即
即![]() 故本题的答案为B.
故本题的答案为B.
12.答案B取特殊值、数形结合
在![]() 中,
中, ![]() ,不妨取A(0,1), C(0,0),B(0,1),则
,不妨取A(0,1), C(0,0),B(0,1),则
∵![]() ∴
∴ ![]() 、
、![]() 、
、![]()
此时![]() 、
、![]() 、
、![]() ;
;![]()
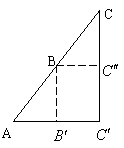 即命题②、③是错误的.
即命题②、③是错误的.
设如图所示共线三点![]() ,
,![]() ,
,![]() ,则
,则
![]()
=![]()
=![]()
![]()
![]()
∴ ![]() 即命题①是正确的.
即命题①是正确的.
综上所述,真命题的个数1个,故本题的答案为B.
13.解:![]() ,
,![]() ,所以
,所以![]() .
.
14.![]() 设
设![]() ,则
,则![]() ,又
,又![]() ,所以由
,所以由![]() 得
得![]() ,于是
,于是![]() ,由
,由![]() 消去m, n得
消去m, n得![]() 的轨迹方程为:
的轨迹方程为:![]() .
.
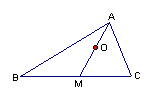 15.
15.![]() 如图,设
如图,设![]() ,则
,则![]() ,所以
,所以![]()
![]()
![]() ,
,
故当![]() 时,
时,![]() 取最小值-2.
取最小值-2.
16.![]() 因为
因为![]() ,所以
,所以![]() .由于点A、B、C能构成三角形,所以
.由于点A、B、C能构成三角形,所以![]() 与
与![]() 不共线,而当
不共线,而当![]() 与
与![]() 共线时,有
共线时,有![]() ,解得
,解得![]() ,故当点A、B、C能构成三角形时实数m满足的条件是
,故当点A、B、C能构成三角形时实数m满足的条件是![]() .
.
17.解析:(1)若![]() 与
与![]() 平行,则有
平行,则有![]() ,因为
,因为![]() ,
,![]() ,所以得
,所以得![]() ,这与
,这与![]() 相矛盾,故
相矛盾,故![]() 与
与![]() 不能平行.
不能平行.
(2)由于![]()
![]() ,又因为
,又因为![]() ,所以
,所以![]() , 于是
, 于是![]() ,当
,当![]() ,即
,即![]() 时取等号.故函数
时取等号.故函数![]() 的最小值等于
的最小值等于![]() .
.
18.解:(Ⅰ)由题意得,f(x)=a·(b+c)=(sinx,-cosx)·(sinx-cosx,sinx-3cosx)
=sin2x-2sinxcosx+3cos2x=2+cos2x-sin2x=2+![]() sin(2x+
sin(2x+![]() ).
).
所以,f(x)的最大值为2+![]() ,最小正周期是
,最小正周期是![]() =
=![]() .
.
(Ⅱ)由sin(2x+![]() )=0得2x+
)=0得2x+![]() =k.
=k.![]() ,即x=
,即x=![]() ,k∈Z,
,k∈Z,
于是d=(![]() ,-2),
,-2),![]() k∈Z.
k∈Z.
因为k为整数,要使![]() 最小,则只有k=1,此时d=(―
最小,则只有k=1,此时d=(―![]() ,―2)即为所求.
,―2)即为所求.
19.解析:解:(Ⅰ)若a⊥b,则sinθ+cosθ=0,
由此得 tanθ=-1(-<θ<),所以 θ=-;
(Ⅱ)由a=(sinθ,1),b=(1,cosθ)得
|a+b|==
=,
当sin(θ+)=1时,a+b取得最大值,即当θ=时,a+b最大值为+1.
20.解:(Ⅰ)由已知得: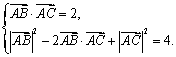 因此,
因此,![]() .
.
(Ⅱ)![]() ,
, ![]()
![]()
![]()
![]()
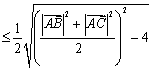
![]() .(当且仅当
.(当且仅当![]() 时,取等号),
时,取等号),
当![]() 的面积取最大值
的面积取最大值![]() 时,
时,![]() ,所以
,所以![]() .
.
解:(I)由条件知: ![]() 且
且![]()
![]() ,
,
设![]() 夹角为
夹角为![]() ,则
,则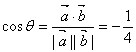 ,
,
![]()
![]() ,故
,故![]() 的夹角为
的夹角为![]() ,
,
(Ⅱ)令![]() 的夹角为
的夹角为![]()
![]()
![]() ,
,
![]()
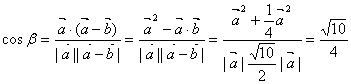
![]()
![]() 的夹角为
的夹角为![]() .
.
21.解析:如图,(Ⅰ)设D(x0,y0),E(xE,yE),M(x,y).由=t, = t ,
知(xD-2,yD-1)=t(-2,-2). ∴ 同理 .
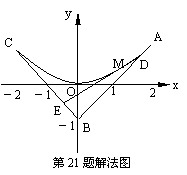 ∴kDE = = = 1-2t.
∴kDE = = = 1-2t.
∴t∈[0,1] , ∴kDE∈[-1,1].
(Ⅱ) 如图, =+ = + t
= + t(-) = (1-t) +t,
=+ = +t = +t(-)
=(1-t) +t,
= += + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2 .
设M点的坐标为(x,y),由=(2,1), =(0,-1), =(-2,1)得
消去t得x2=4y, ∵t∈[0,1], x∈[-2,2].
故所求轨迹方程为: x2=4y, x∈[-2,2]
22.解析:(1)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]()
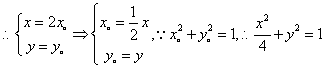 .
.
(2)设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则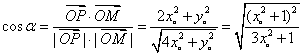 ,
,
令![]() ,则
,则![]() ,
,
当且仅当![]() 时,即
时,即![]() 点坐标为
点坐标为![]() 时,等号成立.
时,等号成立.
![]() 与
与![]() 夹角的最大值是
夹角的最大值是![]() .
.
欢迎访问 http://www.k12zy.com