高三数学排列、组合、二项式、概率与统计

　　

2006－2007学年度上学期

高中学生学科素质训练

高三数学第一轮复习单元测试（9）—

《排列、组合、二项式、概率与统计》

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中。只有一项是符合题目要求的．

1．(理)下列随机变量中，不是离散型随机变量的是　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．从10只编号的球(0号到9号)中任取一只，被取出的球的号码ξ

　　　B．抛掷两个骰子，所得的最大点数ξ

　　　C．[0，10]区间内任一实数与它四舍五人取整后的整数的差值ξ

　　　D．一电信局在未来某日内接到的电话呼叫次数ξ

(文)现有10张奖票，只有1张可中奖，第一人与第十人抽中奖的概率为　　　　　（　　）

　　　A．，　　　　　 B．，　　　　　C．，　 　　　D．，

2．为了让人们感知丢弃塑料袋对环境造成的影响，某班环保小组的六名同学记录了自己家中一周内丢的塑料袋的数量，结果如下(单位：个)：33、25、28、26、25、31．如果该班有45名学生，那么根据提供的数据估计本周全班同学各家共丢弃塑料袋　　　　　　　（　　）

　　　A．900个 　　　　　　　 B．1080个 　　　　　　C．1260个　 　　　　 D．1800个

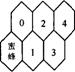3．假定有一排蜂房，形状如图，一只蜜蜂在左下角的蜂房中，由于受了点

伤，只能爬，不能飞，而且只能永远向右方(包括右上，右下)爬行，

从一间蜂房爬到与之相邻的右方蜂房中去，从最初位置爬到4号蜂房

中，则不同的爬法有　　　　　　　　　　　　　　　　  （　　）

　　　A．4种　　 　　　　　B．6种 　　 　　　　　C．8种　　 　 　　　D．10种

4．A与A的大小关系是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　A．A > A　　　　B．A < A　　　　C．A = A　 　　D．大小关系不定

5．(理)若f(m)=，则等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　 A．2　　　　　　　　 B．　 　　　　　C．1　　　　　  　 D．3

　 （文）某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),其中甲和乙不同去,则不同的选派方案共有　　　种

　　 A．1320　　　　　　　 B．288　 　　　　　　 C．1530　　　 　　　 D．670

6．(理)在二项式(x-)⁶的展开式中(其中=－1)，各项系数的和为　　　　　　　　　 （　　）

　　　A．64　　　　　　 B．－64　　　　 C．64 　　　　　　　D．－64

　（文）已知(2a³+)ⁿ的展开式的常数项是第7项，则正整数n的值为　　　　　　　　 （　　）

　　　A．7　　　　　　　　 B．8　　　　　　　 C．9　　　　　 　　 D．10

7．右图中有一个信号源和五个接收器。接收器与信号源在同一个串联线路中时，就能接收

到信号，否则就不能接收到信号。若将图中左端

的六个接线点随机地平均分成三组，将右端的六

个接线点也随机地平均分成三组，再把所有六组

中每组的两个接线点用导线连接，则这五个接收

器能同时接收到信号的概率是　　　　（　　）

A．　　　　　　 B．

　　　 C．　　　　　　 D．

8．（理）同时抛掷4枚均匀的硬币3次，设4枚硬币正好出现2枚正面向上，2枚反面向上的次数为ξ，则　ξ的数学期望是　　　　　  　　　　　　　　　　　　　　　　　　　 （　　）

　　　A．　　　　　　　B．　　　　　　 C．　　　　　　 D．1

　 (文)已知两组数据x₁，x₂，…，x_n与y₁，y₂，…，y_n，它们的平均数分别是和，则新的一组数据2x₁-3y₁+1，2x₂-3y₂+1，…，2x_n-3y_n+1的平均数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．2-3　 　　　 B．2-3+1　　　　C．4-9　　　　　D．4-9+1

9．的展开式中含x的正整数指数幂的项数是　　　　　　　　　　　　　　　　　　　　（　　）

A．0　　　　　　　　 B．2　　　　　　　　 C．4　　　　　　　　 D．6

10．从0到9这10个数字中任意取3个数字组成一个没有重复数字的三位数,这个数不能被3整除的概率为　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．　　　　　　　　　　 B．　　　　　　　　　　 C． 　　　　　　　　　 D． 　　　　　　

11．设集合。选择I的两个非空子集A和B，要使B中最小的数大于A中最大的数，则不同的选择方法共有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．　　　　　 B．　　　　　 C．　　　　 D．

12．某射手射击1次，击中目标的概率是0.9．他连续射击4次，且各次射击是否击中目标相互之间没有影响．有下列结论：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　①他第3次击中目标的概率是0.9　　　　　　 ②他恰好击中目标3次的概率是0.9³×0.1

　　　③他至少击中目标1次的概率是1—0.1⁴

　　　其中正确结论的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．①③　　　 　　　 B．①②　　 　　　　　C．③　　　　　　　　D．①②③

二、填空题：本大题共4小题。每小题4分。共16分　把答案填在题中横线上．

13．二项式(1+sinx)ⁿ的展开式中，末尾两项的系数之和为7，且二项式系数最大的一项的值为，则x在(0，2)内的值为___________．

14．(理)一射手对靶射击，直到第一次中靶为止．他每次射击中靶的概率是0.9，他有3颗子弹，射击结束后剩余子弹数目ξ的数学期望Eξ=______________.

(文)已知某天一工厂甲、乙、丙三个车间生产的产品件数分别是1500、1300、1200，现用分层抽样方法抽取了一个样本容量为n的样本，进行质量检查，已知丙车间抽取了24件产品，则n=____________.

15．某幢楼从二楼到三楼的楼梯共11级，上楼可以一步上一级，也可以一步上两级，若规定从二楼到三楼用7步走完，则上楼梯的方法有___________种．

16．关于二项式(x-1)²⁰⁰⁵有下列命题：

　　④该二项展开式中非常数项的系数和是1：

　　②该二项展开式中第六项为Cx¹⁹⁹⁹；

　　⑧该二项展开式中系数最大的项是第1002项：

　　④当x=2006时，(x-1)²⁰⁰⁵除以2006的余数是2005．

　　其中正确命题的序号是__________．(注：把你认为正确的命题序号都填上)

三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．

17．(本小题满分12分)某人手中有5张扑克牌，其中2张为不同花色的2，3张为不同花色的A，他有5次出牌机会，每次只能出一种点数的牌，但张数不限，此人有多少种不同的出牌方法?

18．(本小题满分12分)求二项式(-)¹⁵的展开式中：

　（1）常数项；

　（2）有几个有理项；

　（3）有几个整式项．

19．(本小题满分12分)(理)在添加剂的搭配使用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时，需要选用两种不同的添加剂。现有芳香度分别为0，1，2，3，4，5的六种添加剂可供选用。根据试验设计原理，通常首先要随机选取两种不同的添加剂进行搭配试验。用表示所选用的两种不同的添加剂的芳香度之和。

（1）写出的分布列；（以列表的形式给出结论，不必写计算过程）

（2）求的数学期望。（要求写出计算过程或说明道理）

（文）在添加剂的搭配使用中，为了找到最佳的搭配方案，需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时，需要选用两种不同的添加剂。现有芳香度分别为0，1，2，3，4，5的六种添加剂可供选用。根据试验设计原理，通常首先要随机选取两种不同的添加剂进行搭配试验。

（1）求所选用的两种不同的添加剂的芳香度之和等于4的概率；

（2）求所选用的两种不同的添加剂的芳香度之和不小于3的概率；

20．(本小题满分12分)袋中装有m个红球和n个白球，m≥n≥2，这些红球和白球除了颜色不同以外，其余都相同．从袋中同时取出2个球．

　（1）若取出是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍，试证：m 必为奇数；

　（2）在肌n的数组中，若取出的球是同色的概率等于不同色的概率，试求m+n≤40的所有数组(m，n)．

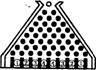21．(本小题满分12分)(理)东方庄家给游人准备了这样一个游戏，他制作了“迷尼游戏板”：在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉，钉子之间留有空隙作为通道，自上而下第1行2个铁钉之间有1个空隙，第2行3个铁钉之间有2个空隙，…，第8行9个铁钉之间有8个空隙(如图所示)．东方庄家的游戏规则是：游人在迷尼板上方口放人一球，每玩一次(放入一球就算玩一次)先付给庄家2元．若小球到达①②③④号球槽，分别奖4元、2元、0元、-2元．(一个玻璃球的滚动方式：通过第1行的空隙向下滚动，小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙．以后小球按类似方式继续往下滚动，落入第8行的某一个空隙后，最后掉入迷尼板下方的相应球槽内)．恰逢周末，某同学看了一个小时，留心数了数，有80人次玩．试用你学过的知识分析，这一小时内庄家是赢是赔；通过计算，你想到了什么?

(文)甲、乙二人做射击游戏，甲、乙射击击中与否是相互独立事件．规则如下：若射击一次击中，则原射击人继续射击；若射击一次不中，就由对方接替射击．已知甲、乙二人射击一次击中的概率均为，且第一次由甲开始射击．

（1）求前3次射击中甲恰好击中2次的概率；

（2）求第4次由甲射击的概率．

22．(本小题满分14分)规定A=x(x-1)…(x-m+1)，其中x∈R，m为正整数，且A=1，这是排列数A(n，m是正整数，且m≤n)的一种推广．

　（1）求A的值；

　（2）排列数的两个性质：①A=nA，②A+mA=A(其中m，n是正整数)．是否都能推广到A(x∈R，m是正整数)的情形?若能推广，写出推广的形式并给予证明；若不能，则说明理由；

　（3）确定函数A的单调区间．

参考答案

1．(理)C　 仅C选项中的差值不是离散型随机变量．

　 (文)C　 无论谁抽中奖的概率均为P==,则第一人与第十人抽中奖的概率均为，故应选C．

2．C  由已知抽样数据可得平均数为=28个，据此可以估计本周全班同学各家共丢弃塑料袋的数量约为28×45=l260个．

3．C　 路线为134；124；1234；0134；0124；01234；024；0234.

4．D　当n≥3时，得-=(n+1)n-n(n-1)(n-2)=-n(n²-4n+1)，当n=3时,-=6>0，得>；当n≥4时，-<0，得<. 即与的关系不定．故应选D．

5．(理)A　∵f(m)=，∴f(3)==(1+3)ⁿ=4ⁿ，f(1)= =(1+1)ⁿ=2ⁿ. ==2,故应选A.

(文)A　用间接法求解简单 ；也可直接法分3类求解；

6．(理)D　令x=l得，各项系数和为(-)⁶=2⁶×(-)⁶=-2⁶=-64．

(文)B　T₇=(2a³)^n-6·a^-6=·2^n-6·a^3n-24，当3n-24=O时，此项为常数项，即n=8时第7项是常数．

7．D　由题意，左端的六个接线点随机地平均分成三组有种分法，同理右端的六个接线点也随机地平均分成三组有种分法；要五个接收器能同时接收到信号，则需五个接收器与信号源串联在同一个线路中，即五个接收器的一个全排列，再将排列后的第一个元素与信号源左端连接，最后一个元素与信号源右端连接，所以符合条件的连接方式共有种，所求的概率是，故选D．

8．(理)B  4枚硬币正好出现2枚正面向上，2枚反面向上的概率为P=C·()⁴=，

　由此可得P(=0)=C·(1-)³=()³，P(=1)=·．(1-)²=，P(=2)=·()²．(1-)=，P(=3)=·()³=，由此可得E=0×()³+1×+2×+3×=．故应选B．

　 (文)B　(2x₁-3y_l+1+2x₂-3y₂+l+…+2x_n-3y_n+1)／n=2(x₁+x₂+…+x_n)／n-3(y₁+y₂+…+y_n)／n+1=2-3+l，故应选B．

9．B 展开式通项为，若展开式中含x的正整数指数幂，即所以，选（B）

10．B将这10个数字按被3除所得的余数分成三个集合A={0,3,6,9},B={1,4,7},C={2,5,8},所以能被3整除的分以下四种情况①三个数都从A中取,共有个数能被3整除;②三个数都从B中取,共有个数能被3整除;③三个数都从C中取,共有个数能被3整除;④分别从ABC中各取一个数,共有个数能被3整除.所以所有能被3整除的数共有228个.而从0到9这10个数字中任意取3个数组成的三位数共有个,所以能被3整除的概率为,于是这个数不能被3整除的概率为,因选B．

11．B 显然，设，则C是I的非空子集，且C中元素不少于2个（当然，也不多于5个）.另一方面，对I的任何一个k（）元子集C，我们可以将C中元素从小到大排列.排好后，相邻数据间共有k1个空档。在任意一个空挡间插入一个隔板，隔板前的元素组成集合A，隔板后元素组成集合B。这样的A、B一定符合条件，且集合对{A，B}无重复.综合以上分析，所求为：.选B.

12．A　恰好击中目标3次的概率是O.9³×0.1，即得②错误，而①③正确，故应选A．

13．或　由已知可得+=n+1=7，即得n=6，二项式系数最大的一项为·sin³x=20sm³x=，解得sinx=，又x∈(0，2)，∴x=或．

14．(理)1.89　 P(=2)=O.9，P(=1)=0.1×0.9=0.09，P(=0)=O.1³+0.1²×0.9=0.0l，由此可得E=2×O.9+l×O.09+O×O.01=1.89．

　 (文)80　每个个体被抽取的概率P==, ∴n=(1500+1300+1200)×=80

15．35　　从二楼到三楼用7步走完，共走11级，则必有4步每步走两级，其余3步每步1级，因此共有=35种方法．

16．①④　二项式(x-1)²⁰⁰⁵所有项的系数和为O，其常数项为-l，非常数项的系数和是1，即得①正确；二项展开式的第六项为x²⁰⁰⁰，即得②错误；二项展开式中系数绝对值最大的项为=，-=-，得系数最大的项是第1003项·x¹⁰⁰³，即③错误；当x=2006时，(x-1)²⁰⁰⁵除以2 006的余数是2006-l=2005，即④正确．故应填①④．

17．由于张数不限，2张2，3张A可以一起出，亦可分几次出，故考虑按此分类． (2分)

　　出牌的方法可分为以下几类：

　　(1)5张牌全部分开出，有A种方法；　　(3分)

　　(2)2张2一起出，3张A一起出，有A种方法；　(4分)

　　(3)2张2一起出，3张A分开出，有A种方法；　(5分)

　　(4)2张2一起出，3张A分两次出，有种方法；　 (7分)

　　(5)2张2分开出，3张A一起出，有A种方法；　(8分)

　　(6)2张2分开出，3张A分两次出，有种方法；　 (10分)

　　因此共有不同的出牌方法A+ A+ A++ A+=860种．　　(12分)

18．展开式的通项为：T_r+1= =

　　(1)设T_r+1项为常数项，则=0，得r=6，即常数项为T₇=2⁶；　　(4分)

　　(2)设T_r+1项为有理项，则=5-r为整数，∴r为6的倍数，又∵0≤r≤15，∴r可取0，6，12三个数，故共有3个有理项．　　(8分)

　　(3) 5-r为非负整数，得r=0或6，∴有两个整式项．　　(12分)

19．(理)解：（１）

	1	2	3	4	5	6	7	8	9
P

（２）

(文)设“所选用的两种不同的添加剂的芳香度之和等于4”的事件为A，“所选用的两种不同的添加剂的芳香度之和不小于3”的事件为B

（１）芳香度之和等于4的取法有2种：、，故。

（２）芳香度之和等于1的取法有1种：；芳香度之和等于2的取法有1种：，故。

20．(1)设取出2个球是红球的概率是取出的球是一红一白2个球的概率的k倍(k为整数)，

　　 则有　　(2分)

∴-kmn=2kn+1．　　(4分)

∵k∈Z，n∈Z，∴m=2kn+1为奇数．　　(6分)

(2)由题意,有，∴=mn,

∴m²-m+n²-n-2mn=0即(m-n)²=m+n，1．　　　　　　　　　　　　 　　(8分)

∴m≥n≥2，所以m+n≥4，∴2≤m-n≤<7，

∴m-n的取值只可能是2，3，4，5，6，相应的m+n的取值分别是4，9，16，25，36，

即或或或或

解得或或或或　　(10分)

　注意到m≥n≥2．

　　∴(m，n)的数组值为(6，3)，(10，6)，(15，10)，(21，15)．　　(12分)

21．(理)游人每玩一次，设东方庄家获利为随机变量(元)；游人每放一球，小球落入球槽，相当于做7次独立重复试验，设这个小球落入铁钉空隙从左到右的次序为随机变量+1，则～B(7，)．

因为P(=-4)=P(=0或=7)=P(=0)+P(=7)=+=

P(=-2)=P(=1或=6)=P(=1)+P(=6)=+=

P(=0)=P(=2或=5)=P(=2)+P(=5)=+=

P(=2)=P(=3或=4)=P(=3)+P(=4)=+=

2+E=2+(-4)×+(-2)×+0×+2×=2+，

一小时内有80人次玩．刚东方庄家通常获纯利为(2+×)80=225(元)

　　 答：庄家当然是赢家!我们应当学会以所学过的知识为武器，劝说人们不要被这类骗子的骗术所迷惑．　 　　　　　　　　　　　　　　　 (12分)

　　(文)假设甲射击命中目标为事件A，乙射击命中目标为事件B．

　  (1)“前3次射击中甲恰好击中2次”其实隐含的条件是：第一次(甲射击)命中、甲在第二次射击也命中、在第三次射击中没有命中，即事件AA发生．事实上，因为第一次(由甲射击)如果出现，则第二次由乙射击，出现B(第三次仍由乙射击)或(第三次改由甲射击)，出现的事件分别为BB，B或A，，都不满足“前3次射击中甲恰好击中2次”，因此第一次(甲射击)命中；再考虑第二次射击，甲如果没有击中，则出现的事件为AB，A也都不满足“前3次射击中甲恰好击中2次”，因此甲在第二次射击也命中；这样第三次不能再命中，否则结果为AAA．前3次射击中甲恰好击中2次可列举为上面事件AA，所求的概率为P=××=；

　 (2)第4次由甲射击隐含条件为：第三次若由甲射击，则必击中；若由乙射击，则必未击中．逆推，可以将问题列举为下列事件：AAA、A、A、B．第4次由甲射击的概率P=()³+()²×+×()²+××=

22．(1)=(-15)(-16)(-17)=4080； 　　　　　　　　　　　　　　 (3分)

(2)性质①、②均可推广，推广的形式分别是

①，②(x∈R，m∈N⁺)

事实上，在①中，当m=1时，左边==x，右边=x=x，等式成立；　　(4分)

当m≥2时，左边=x(x-1)(x-2)…(x-m+1)=x{(x-1)(x-2)…[(x-1)-(m-1)+1]}=x，

因此，①成立； 　　　　　　　　　　　　　　　　　(5分)

在②中，当m=l时，左边=+=x+l==右边，等式成立；

当m≥2时，左边=x(x-1)(x-2)…(x-m+1)+mx(x-1)(x-2)…(x-n+2)

=x(x-1)(x-2)…(x-m+2)[(x-m+1)+m]

=(x+1)x(x-1)(x-2)…[(x+1)-m+1]==右边，　　　　　　　  　　(6分)

因此②(x∈R，m∈N⁺)成立．　　　　　　　　　　 (8分)

(3)先求导数，得()^/=3x²-6x+2．令3x²-6x+2>0，解得x<或x>

因此，当x∈(-∞，)时，函数为增函数，当x∈(，+∞)时，函数也为增函数．　　(11分)

令3x²-6x+2≤0, 解得≤x≤，因此,当x∈[,]时,函数为减函数．　　　　　　 (12分)

∴函数的增区间为(-∞，),(，+∞)；减区间为[,]．

欢迎访问 http://www.k12zy.com