2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(2)— 《数列》
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若互不相等的实数![]() 、
、![]() 、
、![]() 成等差数列,
成等差数列,![]() 、
、![]() 、
、![]() 成等比数列,且
成等比数列,且![]() ,
,
则![]() = ( )
= ( )
A.4 B.2 C.-2 D.-4
2.已知等差数列共有10项,其中奇数项之和15,偶数项之和为30,则其公差是 ( )
A.5 B.4 C.3 D.2
3.在等差数列![]() 中,已知
中,已知![]() 则
则![]() 等于 ( )
等于 ( )
A.40 B.42 C.43 D.45
4.在等差数列{an}中,若aa+ab=12,SN是数列{an}的前n项和,则SN的值为 ( )
A.48 B.54 C.60 D.66
5.设Sn是等差数列{an}的前n项和,若=,则= ( )
A. B. C. D.
6.设![]() 是公差为正数的等差数列,若
是公差为正数的等差数列,若![]() ,
,![]() ,则
,则![]()
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知等差数列{an}的前n项和为Sn,若![]() ,且A、B、C三点共线
,且A、B、C三点共线
(该直线不过原点O),则S200= ( )
A.100 B.101 C.200 D.201
8.在等比数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若数列
,若数列![]() 也是等比数列,则
也是等比数列,则![]() 等于
等于
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.设![]() ,则
,则![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.弹子跳棋共有60棵大小相同的球形弹子,现在棋盘上将它叠成正四面体球垛,使剩下的弹子尽可能的少,那么剩下的弹子有 ( )
A.3 B.4 C.8 D.9
11.设数列![]() 的前n项和为
的前n项和为![]() ,令
,令![]() ,称
,称![]() 为数列
为数列![]() ,
,![]() ,……,
,……,![]() 的“理想数”,已知数列
的“理想数”,已知数列![]() ,
,![]() ,……,
,……,![]() 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, ![]() ,
,![]() ,……,
,……,![]() 的“理想数”为 ( )
的“理想数”为 ( )
A.2002 B.2004 C.2006 D.2008
12.一给定函数![]() 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意![]() ,由关系式
,由关系式![]() 得到的数列
得到的数列![]() 满足
满足![]() ,则该函数的图象是
,则该函数的图象是
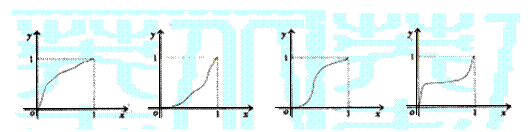 |
A B C D
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13.数列{an}中,若a1=1,an+1=2an+3 (n≥1),则该数列的通项an= .
14.![]() .
.
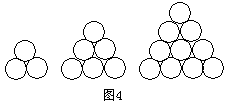 15.在德国不莱梅举行的第48届世乒赛期间,某
15.在德国不莱梅举行的第48届世乒赛期间,某
商场橱窗里用同样的乒乓球堆成若干准“正
三棱锥”形的展品,其中第一堆只有一层,
就一个乒乓球;第2、3、4、…堆最底层(第
一层)分别按图4所示方式固定摆放.从第一
层开始,每层的小球自然垒放在下一层之上,
第n堆第n层就放一个乒乓球,以![]() 表示第n堆的乒乓球总数,则
表示第n堆的乒乓球总数,则
![]() ;
;![]() (答案用n表示).
(答案用n表示).
16.已知整数对排列如下![]() ,
,
则第60个整数对是_______________.
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
数列{an}的前n项和记为Sn,![]()
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且![]() ,又
,又![]() 成等比数列,求Tn
成等比数列,求Tn
18.(本小题满分12分)
设数列![]() 、
、![]() 、
、![]() 满足:
满足:![]() ,
,![]() (n=1,2,3,…),
(n=1,2,3,…),
证明:![]() 为等差数列的充分必要条件是
为等差数列的充分必要条件是![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)
(n=1,2,3,…)
19.(本小题满分12分)
已知数列![]() ,其中
,其中![]() 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() 是公差为
是公差为![]() 的等差数列(
的等差数列(![]() ).
).
(1)若![]() ,求
,求![]() ;
;
(2)试写出![]() 关于
关于![]() 的关系式,并求
的关系式,并求![]() 的取值范围;
的取值范围;
(3)续写已知数列,使得![]() 是公差为
是公差为![]() 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
20.(本小题满分12分)
某市去年11份曾发生流感,据统计,11月1日该市新的流感病毒感染者有20人,此后,每天的新感染者平均比前一天的新感染者增加50人,由于该市医疗部门采取措施,使该种病毒的传播得到控制,从某天起,每天的新感染者平均比前一天的新感染者减少30人,到11月30日止,该市在这30日内感染该病毒的患者总共8670人,问11月几日,该市感染此病毒的新患者人数最多?并求这一天的新患者人数.
21.(本小题满分12分)
等差数列![]() 中,
中,![]() ,公差
,公差![]() 是自然数,等比数列
是自然数,等比数列![]() 中,
中,![]() .
.
(Ⅰ)试找出一个![]() 的值,使
的值,使![]() 的所有项都是
的所有项都是![]() 中的项;再找出一个
中的项;再找出一个![]() 的值,使
的值,使![]() 的项不都是
的项不都是![]() 中的项(不必证明);
中的项(不必证明);
(Ⅱ)判断![]() 时,是否
时,是否![]() 所有的项都是
所有的项都是![]() 中的项, 并证明你的结论;
中的项, 并证明你的结论;
(Ⅲ)探索当且仅当![]() 取怎样的自然数时,
取怎样的自然数时,![]() 的所有项都是
的所有项都是![]() 中的项,并说明理由.
中的项,并说明理由.
22.(本小题满分14分)
已知数列{![]() }中,
}中,![]() (n≥2,
(n≥2,![]() ),
),
(1)若![]() ,数列
,数列![]() 满足
满足![]() (
(![]() ),求证数列{
),求证数列{![]() }是等差数列;
}是等差数列;
(2)若![]() ,求数列{
,求数列{![]() }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)(理做文不做)若![]() ,试证明:
,试证明:![]() .
.
参考答案(2)
1.D.依题意有
![]()
2.C. ![]() ,故选C.
,故选C.
3.B. ∵等差数列![]() 中
中![]() ,
,![]() ∴公差
∴公差![]() .
.
∴![]() =
=![]() =42.
=42.
4.B. 因为![]() ,所以
,所以![]() =54,故选B.
=54,故选B.
5.A. 由等差数列的求和公式可得![]() 且
且![]()
所以![]() ,故选A.
,故选A.
6.B.![]() ,
,![]() ,
,
将![]() 代入,得
代入,得![]() ,从而
,从而![]() .选B.
.选B.
7.A. 依题意,a1+a200=1,故选A.
8.C.因数列![]() 为等比,则
为等比,则![]() ,因数列
,因数列![]() 也是等比数列,则
也是等比数列,则
![]()
即![]() ,所以
,所以![]() ,故选择答案C.
,故选择答案C.
9.D. f(n)=![]() ,选D.
,选D.
10.B. 正四面体的特征和题设构造过程,第k层为k个连续自然数的和,化简通项再裂项用公式求和.依题设第k层正四面体为![]() 则前k层共有
则前k层共有![]() ,k最大为6,剩4,选B.
,k最大为6,剩4,选B.
11.A.认识信息,理解理想数的意义有,
![]() ,选A.
,选A.
12.A.函数认识数列 ![]() ,则函数在
,则函数在![]() 上为凸函数,选A.
上为凸函数,选A.
13.由![]() ,即
,即![]() =2,所以数列{
=2,所以数列{![]() +3}是以(
+3}是以(![]() +3)为首项,以2为公比的等比数列,故
+3)为首项,以2为公比的等比数列,故![]() +3=(
+3=(![]() +3)
+3)![]() ,
,![]() =
=![]() -3.
-3.
14.由![]() ,整体求和所求值为5.
,整体求和所求值为5.
15.![]()
![]() 的规律由
的规律由![]() ,所以
,所以
所以![]()
![]()
16.观察整数对的特点,整数对和为2的1个,和为3的2个,和为4的3个,和为5的4个,和n为的
n-1个,于是,借助![]() 估算,取n=10,则第55个整数对为
估算,取n=10,则第55个整数对为![]() ,注意横
,注意横
坐标递增,纵坐标递减的特点,第60个整数对为![]()
17.(1)由![]() 可得
可得![]() ,两式相减得
,两式相减得![]()
又![]() ∴
∴![]() 故{an}是首项为1,公比为3得等比数列 ∴
故{an}是首项为1,公比为3得等比数列 ∴![]() .
.
(2)设{bn}的公差为d,由![]() 得,可得
得,可得![]() ,可得
,可得![]() ,
,
故可设![]()
又![]() 由题意可得
由题意可得![]() 解得
解得![]()
∵等差数列{bn}的各项为正,∴![]() ,∴
,∴![]() ∴
∴![]()
18.![]() 必要性:设数列
必要性:设数列![]() 是公差为
是公差为![]() 的等差数列,则:
的等差数列,则:
![]()
![]() =
=![]()
![]() =
=![]() -
-![]() =0,
=0,
∴![]() (n=1,2,3,…)成立;
(n=1,2,3,…)成立;
又![]()
![]()
![]() =6
=6![]() (常数)(n=1,2,3,…)
(常数)(n=1,2,3,…)
∴数列![]() 为等差数列.
为等差数列.
![]() 充分性:设数列
充分性:设数列![]() 是公差为
是公差为![]() 的等差数列,且
的等差数列,且![]() (n=1,2,3,…),
(n=1,2,3,…),
∵![]() ……① ∴
……① ∴![]() ……②
……②
①-②得:![]()
![]()
![]() =
=![]()
∵![]()
![]()
∴![]()
![]() ……③ 从而有
……③ 从而有![]()
![]() ……④
……④
④-③得:![]() ……⑤
……⑤
∵![]() ,
,![]() ,
,![]() ,
,
∴由⑤得:![]() (n=1,2,3,…),
(n=1,2,3,…),
由此,不妨设![]() (n=1,2,3,…),则
(n=1,2,3,…),则![]()
![]() (常数)
(常数)
故![]() ……⑥
……⑥
从而![]()
![]() ……⑦
……⑦
⑦-⑥得:![]() ,
,
故![]()
![]() (常数)(n=1,2,3,…),
(常数)(n=1,2,3,…),
∴数列![]() 为等差数列.
为等差数列.
综上所述:![]() 为等差数列的充分必要条件是
为等差数列的充分必要条件是![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…).
(n=1,2,3,…).
19.(1)![]() .
.
(2)![]() ,
, ![]() ,
,
当![]() 时,
时,![]() .
.
(3)所给数列可推广为无穷数列![]() ,其中
,其中![]() 是首项为1,公差为1的等差数列,当
是首项为1,公差为1的等差数列,当![]() 时,数列
时,数列![]() 是公差为
是公差为![]() 的等差数列.
的等差数列.
研究的问题可以是:试写出![]() 关于
关于![]() 的关系式,并求
的关系式,并求![]() 的取值范围.
的取值范围.
研究的结论可以是:由![]() ,
,
依次类推可得 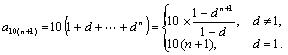
当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() 等.
等.
20.设第n天新患者人数最多,则从n+1天起该市医疗部门采取措施,于是,前n天流感病毒感染者总人数,构成一个首项为20,公差为50的等差数列的n项和,![]() ,而后30-n天的流感病毒感染者总人数,构成一个首项为
,而后30-n天的流感病毒感染者总人数,构成一个首项为![]() ,公差为30,项数为30-n的等差数列的和,
,公差为30,项数为30-n的等差数列的和,![]() 依题设构建方程有,
依题设构建方程有,![]() 化简,
化简,![]() 或
或![]() (舍),第12天的新的患者人数为 20+(12-1)·50=570人.故11月12日,该市感染此病毒的新患者人数最多,新患者人数为570人.
(舍),第12天的新的患者人数为 20+(12-1)·50=570人.故11月12日,该市感染此病毒的新患者人数最多,新患者人数为570人.
21.(1)![]() 时,
时,![]() 的项都是
的项都是![]() 中的项;(任一非负偶数均可);
中的项;(任一非负偶数均可);
![]() 时,
时,![]() 的项不都是
的项不都是![]() 中的项.(任一正奇数均可);
中的项.(任一正奇数均可);
(2) ![]() 时,
时,![]()
![]()
![]()
![]()
![]() 的项一定都是
的项一定都是![]() 中的项
中的项
(3)当且仅当![]() 取
取![]() (即非负偶数)时,
(即非负偶数)时,![]() 的项都是
的项都是![]() 中的项.
中的项.
理由是:①当![]() 时,
时,![]()
![]() 时,
时,
![]() ,其中
,其中![]()
是![]() 的非负整数倍,设为
的非负整数倍,设为![]() (
(![]() ),只要取
),只要取![]() 即(
即(![]() 为正整数)即可得
为正整数)即可得![]() ,
,
即![]() 的项都是
的项都是![]() 中的项;②当
中的项;②当![]() 时,
时,![]() 不是整数,也不可能
不是整数,也不可能
是![]() 的项.
的项.
22.(1)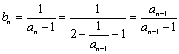 ,而
,而![]() ,∴
,∴![]() .
.![]()
∴{![]() }是首项为
}是首项为![]() ,公差为1的等差数列.
,公差为1的等差数列.
(2)依题意有![]() ,而
,而![]() ,
,
∴![]() .对于函数
.对于函数![]() ,在x>3.5时,y>0,
,在x>3.5时,y>0,![]() ,在(3.5,
,在(3.5,![]() )
)
上为减函数. 故当n=4时,![]() 取最大值3. 而函数
取最大值3. 而函数![]() 在x<3.5时,y<0,
在x<3.5时,y<0,
![]() ,在(
,在(![]() ,3.5)上也为减函数.故当n=3时,取最小值,
,3.5)上也为减函数.故当n=3时,取最小值,![]() =-1.
=-1.
(3)先用数学归纳法证明![]() ,再证明
,再证明![]() . ①当
. ①当![]() 时,
时,![]() 成立;
成立;
②假设当![]() 时命题成立,即
时命题成立,即![]() ,当
,当![]() 时,
时,
![]()
![]()
![]()
![]() 故当
故当![]() 时也成立,
时也成立,
综合①②有,命题对任意![]() 时成立,即
时成立,即![]() .
.
(也可设![]() (1≤
(1≤![]() ≤2),则
≤2),则![]() ,
,
故![]()
![]()
![]() ).
).
下证: ![]()
![]()
![]()
![]() .
.
欢迎访问 http://www.k12zy.com