张家港市后塍高级中学高三数学月考试卷
班级 学号 姓名
1.![]() =
( )
=
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() ,则
,则![]() ( )
( )
A. 在区间(-1,+∞)上是增函数 B. 在区间(-∞,1) 上是增函数
C. 在区间(-1,+∞)上是减函数 D. 在区间(-∞,1) 上是减函数
3.已知点![]() 在不等式组
在不等式组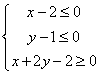 表示的平面区域上运动,则
表示的平面区域上运动,则![]() 的取值范围是
(
)
的取值范围是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知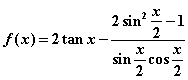 ,则
,则![]() 的值为
( )
的值为
( )
A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
5.若平面四边形ABCD满足![]() ,
,![]() ,则该四边形一定是
( )
,则该四边形一定是
( )
A. 直角梯形 B. 矩形 C. 菱形 D. 正方形
6.已知数列![]() 为等比数列,
为等比数列,![]() ,又第
,又第![]() 项至第
项至第![]() 项的和为112
项的和为112![]() ,
,
则![]() 的值为
( )
的值为
( )
A. 11 B. 12 C. 13 D. 14
7.若![]() 的方差为3,则
的方差为3,则![]() 的标准差为 ( )
的标准差为 ( )
A.12
B.![]() C.16
D.4
C.16
D.4
8.已知抛物线![]() 的焦点恰好是椭圆
的焦点恰好是椭圆![]() 的右焦点
的右焦点![]() ,且两条曲线的交点连线过
,且两条曲线的交点连线过![]() ,则该椭圆的离心率为
( )
,则该椭圆的离心率为
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
9.![]() 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且![]() ,则方程
,则方程![]() 在区间
在区间![]() 内解的个数的最小值是
(
)
内解的个数的最小值是
(
)
A.2 B.3 C.4 D.5
10.意大利数学家斐波那契(L.Fibonacci)在他的1228年版的《算经》一书中记述了有趣的兔子问题:假定每对成年兔子每月能生一对小兔子,而每对小兔子过了一个月就长成了成年兔子,如果不发生死亡,那么由一对成年兔子开始,一年后成年兔子的对数为( )
A.89 B. 233 C.144 D.55
第Ⅱ卷(非选择题,满分100分)
二、填空题:本大题共6小题,每小题5分,共30分,把答案填在相应的横线上。
11.已知![]() 则
则![]() __________.
__________.
12. ![]() 的展开式的第4项是 .
的展开式的第4项是 .
13.已知向量![]() ,其夹角为
,其夹角为![]() ,则直线
,则直线
![]() =0与圆
=0与圆![]() 的位置关系是 ..
的位置关系是 ..
14.若关于x的方程![]() 有三个不同实根,则a的取值范围是________________.
有三个不同实根,则a的取值范围是________________.
15.一台仪器每启动一次都随机地出现一个10位的二进制数![]()
![]() ,其中A的各位数字中,
,其中A的各位数字中,![]() ,
,![]() 出现0的概率为
出现0的概率为![]() ,出现1的概率为
,出现1的概率为![]() ,记
,记![]() ,当启动仪器一次时.则
,当启动仪器一次时.则![]() ,且有且仅有3个1连排在一起时为的概率为 .
,且有且仅有3个1连排在一起时为的概率为 .
16.已知函数![]() (
(![]() )的图像与直线x=a,x=b及x轴所围成图形的面积称为函数
)的图像与直线x=a,x=b及x轴所围成图形的面积称为函数![]() 在
在![]() 上的面积,记为
上的面积,记为![]() ,已知
,已知![]()
![]() ,则
,则![]() _____________.
_____________.
三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)某种人群中各种血型的人所占的比如下表所示:
| 血型 | A | B | AB | O |
| 该血型的人所占比% | 28 | 29 | 8 | 35 |
已知同种血型的人可以输血,O型血可以输给任一种血型的人,任何人的血都可以输给AB型血的人,其他不同血型的人不能互相输血。小王是B型血,若小王因病需要输血,问:
(1)任找一人,其血可以输给小王的概率是多少?
(2)任找一人,其血不能输给小王的概率是多少?
18.(本小题满分12分)设函数![]() 点
点
![]()
![]() 为
为![]() .
.
(1)若![]() 的表达式;
的表达式;
(2)在(1)的条件下,求![]() 上的最大值
上的最大值
19.(本小题满分14分,第一小问满分3分,第二小问满分5分,第三小问满分6分)
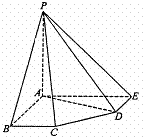 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=![]() a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
(1)求证:PA⊥平面ABCDE;
(2)求二面角A-PD-E的大小;
(3)求点C到平面PDE的距离.
20.(本小题满分16分)设![]() 。
。
(1)是否存在常数p,q,使![]() 为等比数列?若存在,求出p,q的值。若不存在,说明理由;
为等比数列?若存在,求出p,q的值。若不存在,说明理由;
(2)求![]() 的通项公式;
的通项公式;
(3)当![]() 时,证明:
时,证明:![]() 。
。
21.(本小题满分15分)如图椭圆C的方程为![]() ,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,
,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,
△APB的面积为![]() .
.
(1) 求椭圆C的方程;
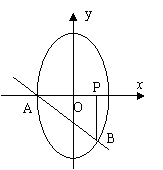 (2) 在直线AB上求一点M,使得以椭圆C的焦点为焦点,且过M的双曲线E的实轴最长,并求此双曲线E的方程.
(2) 在直线AB上求一点M,使得以椭圆C的焦点为焦点,且过M的双曲线E的实轴最长,并求此双曲线E的方程.
数 学 参考答案
一、选择题:本大题共10小题,每小题5分,共50分。
1.D 2.B 3.C 4.D 5.C 6.D 7.B 8.A 9.D 10.B
二、填空题:本大题共6小题,每小题5分,共30分
11. ![]() 12.
12.![]() 13.相离; 14.
13.相离; 14.![]() 15.
15.![]() 16.
16.![]()
三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
解:对任一人,其血型为A,B,AB,O型血的事件分别记为![]() ,它们是互斥的。由已知有:
,它们是互斥的。由已知有:
![]() ,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件
,因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件![]() ,根据互斥事件的加法公式有:
,根据互斥事件的加法公式有:
![]() =0.29+0.35=0.64
=0.29+0.35=0.64
(2)由于A,AB型血不能输给B型血的人,故“不能输给B型血的人”为事件![]() ,
,
![]() =0.28+0.08=0.36
=0.28+0.08=0.36
答:任找一人,其血可以输给小王的概率是0.64,任找一人,其血不能输给小王的概率是0.36
18.(本小题满分14分)
(1)由函数![]() ,求导数得
,求导数得![]() ,
,
过![]()
![]()
![]()
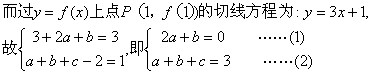
![]()
![]()
(2)![]()
![]()
| x |
| -2 |
|
|
|
|
|
| 0 | - | 0 | + |
|
| 极大 |
| 极小 |
|
有表格或者分析说明
![]()
![]()
![]() ,
,![]() 上最大值为13
上最大值为13 ![]()
19.(1)证明∵PA=AB=2a,PB=2![]() a,∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
a,∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
同理PA⊥AE.3分∵AB∩AE=A,∴PA⊥平面ABCDE. …………… 4分
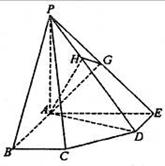 (2)∵∠AED=90°,∴AE⊥ED.
(2)∵∠AED=90°,∴AE⊥ED.
∵PA⊥平面ABCDE,∴PA⊥ED.
∴ED⊥平面PAE.过A作AG⊥PE于G,
∴DE⊥AG,∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角. ……… 7分
在直角△PAE中,AG=![]() a.在直角△PAD中,AH=
a.在直角△PAD中,AH=![]() a,
a,
∴在直角△AHG中,sin∠AHG=![]() =
=![]() .∴∠AHG=arcsin
.∴∠AHG=arcsin![]() .
.
∴二面角A-PD-E的大小为arcsin![]() . ……… 9分
. ……… 9分
(3)∵∠EAB=∠ABC=∠DEA=90°, BC=DE=a,AB=AE=2a,
取AE中点F,连CF,
∵AF∥=BC, ∴四边形ABCF为平行四边形.
∴CF∥AB,而AB∥DE, ∴CF∥DE,而DE![]() 平面PDE,CF
平面PDE,CF![]() 平面PDE,
平面PDE,
∴CF∥平面PDE.
∴点C到平面PDE的距离等于F到平面PDE的距离. ………10分
∵PA⊥平面ABCDE, ∴PA⊥DE. 又∵DE⊥AE,∴DE⊥平面PAE.
∴平面PAE⊥平面PDE.
∴过F作FG⊥PE于G,则FG⊥平面PDE.
∴FG的长即F点到平面PDE的距离. ………13分
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,
∴FG=![]() a. ∴点C到平面PDE的距离为
a. ∴点C到平面PDE的距离为![]() a. …… 15分
a. …… 15分
20.(本小题满分14分)
解:(1)由![]() 得:
得:![]()
可见:应有![]()
![]()
因此存在常数![]() 使
使![]() 为等比数列。
为等比数列。
(2)由于![]() 是以
是以![]() 为首项2为公比的等比数列
为首项2为公比的等比数列
![]()
![]()
(3)当![]() 时,
时,![]()
![]() 。
。
而![]()
![]()
![]() (
(![]() )
)
![]()
![]() 当
当![]() 时,
时,![]() 。
。
21.(1) ![]() 又∠PAB=45°,AP=PB,故AP=BP=3.
又∠PAB=45°,AP=PB,故AP=BP=3.
∵P(1,0),A(-2,0),B(1,-3)![]() 分
分
∴ b=2,将B(1,-3)代入椭圆得: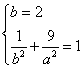 得
得![]() ,
,
所求椭圆方程为![]() .
. ![]()
(2)设椭圆C的焦点为F1,F2,
则易知F1(0,-![]() )F2(0,
)F2(0,![]() ),
),![]()
直线![]() 的方程为:
的方程为:![]() ,因为M在双曲线E上,要双曲线E的实轴最大,只须||MF1|-|MF2||最大,设F1(0,-
,因为M在双曲线E上,要双曲线E的实轴最大,只须||MF1|-|MF2||最大,设F1(0,-![]() )关于直线
)关于直线![]() 的对称点为
的对称点为
![]() (
(![]() -2,-2),则直线
-2,-2),则直线![]() 与直线的交点为所求M,
与直线的交点为所求M,![]()
因为![]() 的方程为:
的方程为:![]() ,联立
,联立
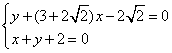 得M(
得M(![]() )
) ![]() 分
分
又![]() =||MF1|-|MF2||=||M
=||MF1|-|MF2||=||M![]() |-|MF2||
|-|MF2||![]()
=![]() =2
=2![]() ,故
,故![]() ,
,
故所求双曲线方程为: ![]()
![]() 分
分