冷水江市一中2007届高三第十次模拟考试
理科数学试卷
命题:杨玉林 审题:李康华
一、选择题:本大题共10个小题,每小题5分,共50分
1.定义运算![]() ,则符合条件
,则符合条件![]() (
(![]() 为虚数单位)的复数
为虚数单位)的复数
![]() 为 ( )
为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
|
2.一植物园参观路径如右图所示,若要全部参观并且路线不重复,
则不同的参观路线种数共有 ( )
A.48种 B.36种
C.12种 D.6种
3.在△ABC中,tanA是第3项为-4、第7项为4的等差数列的公差,tanB是第3项为![]() ,第6项为9的等比数列的公比,则△ABC是
( )
,第6项为9的等比数列的公比,则△ABC是
( )
A.等腰三角形 B.锐角三角形
C.直角三角形 D.钝角三角形
4.若两个函数的图像经过若干次平移后能够重合,则称这两个函数为“同形”函数.
给出下列三个函数:![]() ,
,![]() ,
,![]() ,
,
则 ( )
A.![]() 为“同形”函数
为“同形”函数
B.![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
C.![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
D.![]() 为“同形”函数,且它们与
为“同形”函数,且它们与![]() 不为“同形”函数
不为“同形”函数
5、已知![]() 为
为![]() 的垂心,下列结论一定成立的是
( )
的垂心,下列结论一定成立的是
( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
6.设f(x)是定义在R上的偶函数,当x>0时,f(x)+x![]() >0,且f(1)=0,则不等式x·f(x)>0的解集为 (
)
>0,且f(1)=0,则不等式x·f(x)>0的解集为 (
)
A.(-![]() ,-1)∪(1,+
,-1)∪(1,+![]() ) B.(-1,0)∪(0,1)
) B.(-1,0)∪(0,1)
C.(-1,0)∪(1,+![]() )
D.(-
)
D.(-![]() ,-1)∪(0,1)
,-1)∪(0,1)
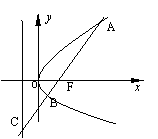
 7.在长方体
7.在长方体![]() 中,
中,![]() ,点
,点![]() 分
分
别在棱![]() 、
、![]() 上滑动,且线段
上滑动,且线段![]() 的长恒等于2,则线段
的长恒等于2,则线段![]() 的中点
的中点![]() 的轨迹是
( )
的轨迹是
( )
A、圆的一部分 B、椭圆的一部分
C、双曲线的一部分 D、抛物线的一部分
8.已知函数![]() 的反函数
的反函数![]() 的图象的对称中心是(b,3),则不等式
的图象的对称中心是(b,3),则不等式![]() 的解集是
( )
的解集是
( )
A.(-3,4) B.![]()
C.(2,3) D.![]()
 9.如图,过抛物线
9.如图,过抛物线![]() 的焦点F的直线
的焦点F的直线![]() 交抛物线于点A、B,交其准线于点C,若
交抛物线于点A、B,交其准线于点C,若![]() ,且
,且![]() ,则此抛物线的方程为
( )
,则此抛物线的方程为
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.设M是![]()
m、n、p分别是![]() 的最小值是
( )
的最小值是
( )
A.8 B.9 C.16 D.18
二、填空题:本大题共5个小题,共25分,将答案填写在题中的横线上
11.设![]() ,
,
则![]() +
+![]() =
.
=
.
12.设数列![]() 满足
满足![]() ,且
,且![]() ,
,![]()
求 ![]() =
=
13.正三棱锥S—ABC内接于球O,且球心O在平面ABC上.若正三棱锥A—ABC的底面边
| |
14.定义![]() ,设实数
,设实数![]() 满足约束条件
满足约束条件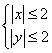
![]() ,
,![]() ,则
,则![]() 的取值范围是
的取值范围是
15.设函数![]() ,给出下列四个命题
,给出下列四个命题
①若c=0,则f(x)为奇函数;
②若b=0,c>0,则方程f(x)=0只有一个实根;
③函数y= f(x)的图象关于点(O,C)成中心对称图形;
④关于x的方程f(x)=0最多有两个实根.
其中正确的命题是
三、解答题:本大题共6个小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
在一次语文测试中, 有道把我国四大文学名著《水浒传》、《三国演义》、《西游记》、《红楼梦》与它们的作者连线的题目, 每连对一个得3分, 连错不得分, 一位同学该题得ξ分.
(1)求该同学得分不少于6分的概率;
(2)求ξ的分布列及数学期望.
17. (本小题满分12分)
已知A、B、C为△ABC的三内角,其对边分别为a、b、c.
若=(-cos,sin),=(cos,sin),a=2,且·=.
(1)若三角形ABC的面积S=,求b+c的值;
(2)求b+c的取值范围.
18.(本小题满分12分)
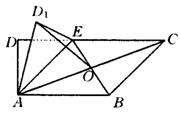
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上一点,满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点![]() 。
。
(1)判断平面D1AE与平面ABCE是否垂直?并说明理由.
(2)求异面直线OD1与AE所成角的余弦值;
19.(本小题满分12分)
已知“接龙等差”数列![]() 构成如下:
构成如下:![]() ,
, ![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() 是公差为
是公差为![]() 的等差数列;
的等差数列;![]() ;
;![]() 是公差为
是公差为![]() 的等差数列(
的等差数列(![]() );其中
);其中![]() .
.
(1) 若![]() ,求
,求![]() ;
(2) 设
;
(2) 设![]() .求
.求![]() ;
;
(3) 当![]() 时,证明对所有奇数
时,证明对所有奇数![]() 总有
总有![]() .
.
20.(本小题满分13分)
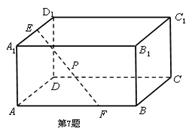
如图![]() 为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点,
为双曲线E的两焦点,以F1F2为直径的圆O与双曲线E交于M、N、M1、N1,B是圆O与y轴的交点,连接MM1与OB交于H,且H是OB的中点,
|
(2)试证:对任意的正实数c,双曲线E的
离心率为常数; (4分)
(3)连接F1M与双曲线E交于点A,是否存在
常数![]() 恒成立,若存在试求出
恒成立,若存在试求出
![]() 的值;若不存在,请说明理由。 (5分)
的值;若不存在,请说明理由。 (5分)
21.(本小题满分14分)
已知函数![]()
(1)![]()
![]() 的根,β是方程xex =2007的根,求α
的根,β是方程xex =2007的根,求α![]() β的值。
β的值。
(4分)
(2)求证:在区间(1,![]() )上,函数
)上,函数![]() 图象在函数
图象在函数![]() 图象的下方;(5分)
图象的下方;(5分)
(3)设函数![]() ,求证:
,求证:![]() ≥
≥![]() .
(5分)
.
(5分)