高三年级大联考试卷数学文科

浙江省五市2007年4月高三年级大联考试卷

　 数学文科　　 2007．4

本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟。

第I卷(选择题 共50分)

一、选择题：(本大10题小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目 要求的。)

1.若全集U={1，2，3，4}，A={1，2，3}，B={2，3}，则C_U(A∩B)为

 A.{1，4}　　　　　　　　　　B.{2，3}　　　　　　　　　　　C.{1，2，3}　　　　　　　　D.{4}

2.已知数列{a_n}是等差数列，且a₃+a₁₁=50,又a₄=13,则a₂等于

 A.1　　　　　　　　　　　　　　　　　 B.4　　　　　　　　　　　　　　　C.5　　　　　　　　　　　　　　　D.6

3.由线的中心到直线的距离是

 A.　　　　　　　　　　　　　B.　　　　　　　　　　　　 C.1　　　　　　　　　　　　　　　D.

4.锐角α满足sinα·cosα=,则tanα的值为

 A.2-　　　　　　　　　　 B. 　　　　　　　　　　　　C.2±　　　　　　　　　　 D.2+

5.已知直线m,n和平面α,则m∥n的一个必要非充分条件是

 A. m∥α、n∥α　　　 B.m⊥α、n⊥α　　　　　C.m∥α、nα　　　　 D.m、n与α成等角

6.设a，b是两个非零向量，若8a-kb与-ka+b共线，则实数k值为

 A.2　　　　　　　　　　　B.-2　　　　　　　　　　　 C.±2　　　　　　　　　　D.8

7.6个人站成前后二排，每排三人，其中甲不站在前排，乙不站在后排的站法种数为

 A.72　　　　　　　　　　　　　 B.216　　　　　　　　　　　　　 C.360　　　　　　　　　　　　　 D.108

8.已知函数y=f(x)的图象和y=sin(x+)的图象关于点P(，0)对称，则f(x)的表达式是

 A.cos(x+)　　　　　　　 B.-cos(x-)　　　　　　　　C.-cos(x+)　　　　　　　 D.cos(x-)

9.在正方体ABCD—A₁B₁C₁D₁的侧面AB₁内有一个动点P到直线A₁B₁与直线BC的距离相等，则动点P所在曲线的形状大致为

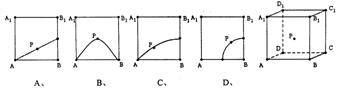10.直线l：A_x+B_y+C=0过一、二、四象限，坐标原点O(0，0)与点M(m,n)同在直线l的左下方，则A_m+B_n+C的值

 A.与A同号，与B同号　　　　　　　　　　　　　　　　 B.与A同号，与B异号

 C.与A异号，与B同号　　　　　　　　　　　　　　　　 D.与A异号，与B异号

第Ⅱ卷(非选择题 共100分)

二、填空题：(本大题共4小题，每小题4分，共16分)

11.若(3x-1)ⁿ(n∈N*)展开式中各项系数之和为128，则展开式中x²的系数为　　　　

12.在120°的二面角内放一个半径为5的球，切两个半平面于A、B两点，

　 则这两个切点在球面上的球面距离是　　　　.

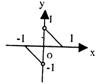
13.已知函数f(x)的图象是两条直线的一部分，其定义域为

　 [-1,0]∪(0,1),则不等式f(x)-f(-x)>-1的解集是　　　　　  .

14.某种细胞开始时有2个，一小时后分裂成4个并死去1个，两小时后分裂成6个并死去1个，三个小时后分裂成10个并死去1个，……按照这种规律进行下去，100小时后细胞的存活数是　　　.

三、解答题：(本大题共6小题，每小题14分，共84分。)

15.已知二次函数f(x)=x²-2x+6,设向量a=(sinx,2),b=(2sinx,),c=(cos2x,1),d=(1,2).

　(1)分别求a·b和c·d的取值范围；

　(2)当x∈[0，π]时，求不等式f(a·b)>f(c·d)的解集。

16.已知数列{a_n}的首项a₁=1，其前n项和为S_n，且对任意正整数n,有n,a_n,S_n成等差数列

　(1)求证：数列{S_n+n+2}成等比数列

　(2)求数列{a_n}的通项公式

17.某商家进行促销活动，促销方案是：顾客每消费1000元，便可以获得奖券一张，每张奖券中奖的概率为，若中奖商家返还顾客现金1000多元。小王购买 一套价格为2400元的西服，只能得到2张奖券，于是小王补偿20元给一同事购买一件价格为600元的便服，这样小王就得到了3张奖券。

 (1)求商家恰好返还小王现金1000元的概率；

 (2)求商家至少返还小王现金1000元的概率；

 (3)试说明小王出资20元增加1张奖券是否划算？

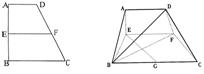18.已知梯形ABCD中，AD∥BC，∠ABC=∠BAD=，AB=BC=2AD=4，E、F分别是AB、CD上的点，EF∥BC，AE=x，G是BC的中点。沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF(如图)。

  (1)当x=2时，求证：BD⊥EG；

  (2)若以F、B、C、D为顶点的三棱锥的体积记为f(x),求f(x)的最大值；

  (3)当f(x)取得最大值时，求二面角D-BF-C的正切值。

19.已知点A(-5，0)，B(5，0)，动点P满足8成等差数列

  (1)求点P的轨迹方程；

　(2)对于x轴上的点M，若满足，则称点M为点P对应的“比例点”，求证：对任意一个确定的点P，它总对应两个“比例点”。

20.已知f(x)=x³+ax²+bx+c在x=1处，都取得极值

(1)求a、b的值；

(2)求f(x)的单调增区间；

(3)若对任意x∈[-1,2],f(x)<恒成立，求实数c的取值范围。

参考答案

一、选择题(每小题5分)

小题号	1	2	3	4	5	6	7	8	9	10
答案	A	C	A	C	D	C	B	B	C	D

二、填空题(每小题4分)

11.-189　　　　　　　　　　 12.　　　　　 13.-1≤x<-或0<x≤1　　　　　　　14.2¹⁰⁰+1

三、解答题(每小题14分，共84分)

15.解：(1)a·b=2sin²x+1≥1　　　　　　　c·d=cos²x+1≥1　　　　　　　　　　　　……6分

(2)∵f(x)图象关于x=1对称，∴f(x)在(1,+∞)内单调递增。

由f(a·b)>f(c·d)a·b>c·d,　即2sin²x+1>2cos²x+1

又∵x∈[0，π] ∴x∈()

故不等式的解集为()　　　　　　　　　　　　　　　　　　　　　　　 ……8分

16.解：(1)∵n,a_n,Sn成等差数列　　 ∴2a_n=n+S_n

又a_n=S_n-S_n-1(n≥2)

∴2(S_n-S_n-1)=n+S_n　　　　　　　　 即S_n=2S_n-1+n

∴S_n+n+2=2S_n-1+2(n+1)=2[S_n-1+2(n-1)+2]　且S₁+1+2=4≠0

∴{S_n+n+2}是等比数列　　　　　　　　　　　　　　　　　　　　　　　　　……7分

(2)∵S_n+n+2=4·2^n-1=2ⁿ⁺¹　　　　　　　　　 ∴S_n=2ⁿ⁺¹-n-2

∴a_n=S_n-S_n-1=2ⁿ-1

又当n=1时，a₁=S₁=1=2¹-1　∴a_n=2ⁿ-1　　　　　　　　　　　　　 ……7分

17.解：(1)商家恰好返还小王现金1000元，即小王的3张奖券有且只有1张中奖.

  P=C　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……4分

  (2)设商家至少返还小王现金1000元为事件A，小王的3张奖券有且只有1张中奖为事件A₁，有且只有2张中奖为事件A₂，3张全中奖为事件A₃，则A=A₁+A₂+A₃，A₁、A₂、A₃为互斥事件。

  P(A)=P(A₁)+P(A₂)+P(A₃)=C

=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……6分

(用“对立事件”发生的概率从反面求解，请相应给分)

(3)设小王不出资20元增加1张奖券消费情况下商家至少返还小王现金1000元为事件B，小王的3张奖券有且只有1张中奖为事件B₁，2张全中奖为事件B₂，则B=B₁+B₂，B₁、B₂为互斥事件。

P(B)=P(B₁)+P(B₂)=C

P(A)>P(B)，故从增加中奖概率来看小王出资20元增加1张券是划算的　　　 ……4分

18.(1)证明：过D作DH⊥EF于H，连BH，HG，则四边形BGHE为正方形，BH⊥EG,

  ∴BD⊥EG;　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……4分

(2)解：f(x)=V_D-FBC=

　当且仅当x=2时取等号，所以f(x)的最大值为　　　　　　……4分

(3)解：过H作HM⊥BF于M,连DM，则∠DMH为二面角D-BF-C的平面角的补角，

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　……2分

在△DHM中，DH=2，HM=∴tan∠DHM=

所求二面角D-BF-C的正切值为-　　　　　　　　　　　　　　　 ……4分

19.解：(1)(x≥4)　　　　　　　　　　　　　　　　　　　　　　　　　　　　……6分

(2)证明：设P(x₀,y₀)(x₀≥4),M(m,0)

∵e=　　　　　　　　　　　　　……3分

又∵　　 ……2分

由得m²-2mx₀+7=0　　　　　　　∴△=4x₀²-28≥64-28>0

∴对于点P它总对应两个比例点　　　　　　　　　　　　　　　 ……3分

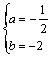20.解：(1)f′(x)=3x²+2ax+b=0两-和1　　　　 ∴　　 ……4分

(2)∵f′(x)=(3x+2)(x-1)

∴当x∈[-1，-]时，f′(x)>0；当x∈(-,1)时，f′(x)<0；当x∈(1，2)时，f′(x)>0.

∴f(x)的单调递增区间为[-1，-]和(1，2)　　　　　　　　　　　　　　　　　　　……5分

(3)由(2)知当x=-时，f(x)有极大值

又f(2)=2+C>,f(-1)=+<

∴x∈[-1，2]时，f(x)最大值为f(2)=2+C

∴C²>2+C　　　　 ∴C<-1或C>2　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……5分