湖南师大附中2007届高三年级月考七理科数学
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）
如果事件A在依次实验中发生的概率是P，那么n次独立重复实验中恰好发生k次的概率
球的体积公式V球=
，球的表面积公式 S=4
，其中R表示球的半径
一、选择题（本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的.
1．若集合A={1，2，3}，则满足A∪B=A的非空集合B的个数是
A．6 B．7 C．8 D．9
2．已知
A．在区间（－1，+∞）上是增函数
B．在区间（－∞，1）上是增函数
C．在区间（－1，+∞）上是减函数
D．在区间（1，+∞）上是减函数
3．对于直线m、n和平面α，下列命题中的真命题是
A．若m//α，n//α，m、n共面，则m//n
B．若m
α，n//α，m、n共面，则m//n
C．若mα，n
α，m、n异面，则n//α
D．若mα，nα，m、n异面，则n与α相交
4．设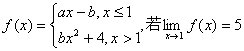
，则常数a的值为
A．1 B．6 C．9 D．10
5．过△ABC的重心G作一直线分别交AB、AC于D、E，若
，则
的值为
A．1 B．2 C．3 D．4
6．在直角坐标平面上，以（199，0）为圆心，199为半径的圆周上整点的个数为
A．2 B．4 C．8 D．无数个
7．已知
动圆P与其中一个圆内切，而与另一个圆外切，则动圆圆心P的轨迹方程为
| |
B．
C．（
D．（
8．已知{an}为等差数列，{bn}为等比数列，其公比q≠1，且
，若a1=b1，a11=b11，则
A．a6＞b6 B．a6=b6 C．a6＜b6 D．a6＞b6或a6＜b6
9．命题
的
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
10．已知F1、F2为椭圆的左、右焦点，抛物线C以F1为顶点，F2为焦点，设P为椭圆与抛物线的一个交点，如果椭圆的离心率e满足PF1=ePF2，则e的值是
A．
B．
C．
D．
二、填空题：本大题共5小题，每小题5分，共25分.
11．两个集合A与B之差记作“A/B”，其定义为：A/B={xx∈A，且x∈B}，如果集合A=
若A/B=O，则m的取值范围为
.
12．已知点A（2，－3）、B（－3，－2），若直线l过点P（1，1）且与线段AB相交，则直线l的斜率k的取值范围是 .
13．将直线
沿x轴向左平移一个单位，所得直线与圆
相切，则实数
的值为
.
14．从8名超级女生中选派4名同时去4个地区演出（每地1人），其中甲和乙只能同去或同不去，甲和丙不同去，则不同的选派方案共有 种.
15．在正方形ABCD中，E、F分别是AB、CD的中点，沿EF将正方形折成120°的二面角，则异面直线BF与DE所成角的余弦值是 .
三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤.
16．（本小题满分12分）
设函数
（1）求函数f（x）的解析式；
（2）将函数f（x）的图象按向量
平移，使得平移后的图象关于原点对称，求向量c
| |
17．甲乙两人参加一次英语口语考试，已知在备选的10道题中，甲能答对其中的6道题，乙能答对其中的8道题，规定每位考生都从备选题中随机抽出3道题进行测试，至少答对2道题才算合格。
（1）求甲、乙两人考试合格的概率分别是多少；
（2）求乙答对试题数
的概率分布与数学期望.
18．（本小题满分12分）
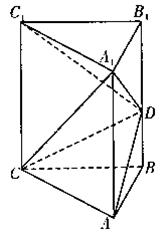
如图，直三棱柱ABC—A1B1C1中，AB=AC=1，AA1=2，∠BAC=90°，D为棱BB1的中点.
|
（2）求直线C1D与面ACD所成的角的大小.
19．（本小题满分12分）
在交通拥挤及事故多发地段，为了确保交通安全，规定在此地段内，车距d是车速v（千米/时）的平方与车身长s（米）的积的正比例函数，且最小车距不得小于车身长的一半.现假定车速为50（千米/时），车距恰为车身长.
（1）试写出d关于v的分段函数解析式（其中s为常数）
（2）应规定怎样的车速，才能使此地段的车流量
最大
20．设Sn为等差数列{an}的前n项和（n∈N*）
（1）若数列{an}单调递增，且a2是a1、a5的等比中项，求证：
（2）数列{an}的公差为d，且
问是否存在正的常数c，使得等式
对任意正整数n都成立.若存在，求c（用d表示）；若不存在，请说明理由.
21．（本小题满分14分）
点P在双曲线
右支上，F是该双曲线的右焦点，点M为线段PF的中点，若OM=OF=3，M到右准线l的距离为
（1）求双曲线的方程；
（2）设过点P的直线与两渐近线
分别交于点P1、P2，点P分有向线段
OP1·OP2的最小值与最大值.
参考答案
一、选择题：本大题共有10小题，每小题5分，共50分。在每小题给出的四个选项中有且只有一项是符合题目要求的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | D | B | B | C | B | C | A | A | C |
二、 填空题：本大题共5小题，每小题5分，共25分.
11．
12． 
13．7或－3 14．600 15．
三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤.
16．解：（1）
…3分
当a＞0时，
由题意得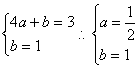
…………………………………………5分
∴函数f（x）的解析式为
……………………6分
（2）由图象变换得
……………………8分
∵平移后的图象关于原点对称
∴g（0）=0且2+k=0………………………………………………………………10分
又
………………………………………………12分
17．解：（1）设A={甲考试合格}，B={乙考试合格}，
………………………………………………3分
………………………………………………6分
（2）
……9分
所以乙答对试题数的概率分布如下：
|
| 1 | 2 | 3 |
| P |
|
|
|
乙答对试题数的数学期望
………………12分
18．解：（1）证明：在直三棱柱中，∠BAC=90°
∴AC⊥面ABB1A1，
则AC⊥A1D………………………………………………………………………………2分
又AD=
则AD2+A1D2=AA12
于是AD⊥A1D………………………………………………………………4分
∴A1D⊥面ACD………………………………………………………………6分
又A1D面A1DC
∴平面A1DC⊥平面ADC
（2）取CC1中点E，连结BE交CD与点F，
则BE//C1D
C1D与面ACD所成角的大小等于BE与面ACD所成角的大小…………7分
取AD中点G，连结BG，FG，则等腰△ABD中，
AD⊥BG……………………………………………………………………8分
又由（1）得AC⊥面ABB1A，
∴AC⊥BG
∴BG⊥面ACD
∴∠BFG为直线BE与面ACD所成的角……………………………………10分
又
………………………………………………11分
∴直线C1D与平面ACD所成的角为
………………………………12分
19．解：（1）由题意，设
……………………………………………………1分
∵v=50时，d=s，
……………………………………………………3分
又当
……………………………………………………4分
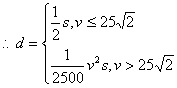………………………………………………6分
（2）由题意，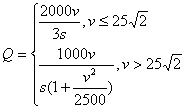
………………………………8分
当
………………9分
当
时
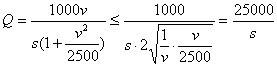此时v=50……………………11分
又
，故当v=50千米/时时车流量Q最大……………………12分
20．解：记等差数列{an}的公差为d，由题意得
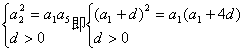
解得d=2a1……………………………………………………………………………2分
所以
………………………………4分
于是
故……………………………………………………6分
（2）假设存在正常数c，使得等式恒成立……7分
又
………………8分
所以当n=1时，有
整理变形得
两边平方化简得
………………………………………………………… 10分
接下来证明：当时，对任意正整数n都成立
∴存在正常数
使得等式对任意正整数n都成立………………13分
21．解：（1）依题意得c=3
设双曲线左焦点为F‘，连P F‘，则P F‘=2OM=6
由双曲线定义可得PF=6－2a
过点P、M作PQ⊥l，MN⊥l，垂足分别为Q、N
又设OF与l相交于点G，则
…………………………4分
由梯形中位线性质得：PQ=2MN－FG
又ePQ=PF，
∴
，
从而可得
（舍去）………………6分
…………………………8分
（2）由（1）得，该双曲线的渐近线方程为
设P（x，y），P1（x1，y1），P2（x2，y2），则
因为点P分
……………………………………………………………………………………9分
∵点P（x，y）在双曲线
上，
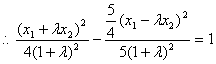
化简得
…………………………………………10分
·
…………………………………………12分
令
在（0，1）上为减函数，在（1，+∞）为增函数，
故得OP1OP2的最小值为9，最大值为
………………………………14分