2007年潍坊市高三统一考试
数学试题(理工农医学)
本试卷第I卷(选择题)和第II卷(非选择题)两部分。第I卷1至4页,第II卷5至11页,共150分。考试时间120分钟。
第I卷(选择题 共60分)
注意事项:
1. 答第I卷前,考生务必将自己的姓名、准考证号、考试科目铅笔涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,在选涂其他答案,不能答在试题卷上。
3. 考试结束,监考人将本试卷和答题卡一并收回。
参考公式: 正棱锥、圆锥的侧面公式
如果事件A、B互斥,那么
![]()
![]()
如果事件A、B相互独立,那么 其中c表示底面周长,l表示斜高母线长
![]() 球的体积公式
球的体积公式
如果事件A在一次试验中发生的
![]()
概率是P,那么n次独立重复试验 其中R表示球的半径
中恰好发生k次的概率
![]()
一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. ![]() ,若
,若![]() 为实数,则a的值为
为实数,则a的值为
A.0 B.1 C.2 D.不存在
2.集合![]() ,定义一种运算
,定义一种运算![]() :若
:若![]() ,则
,则![]() .那么预算
.那么预算![]() 可以是
可以是
A.加法 B.减法 C.乘法 D.除法
3.设命题p,q为简单命题,则“![]() 为真”是“
为真”是“![]() 为真”的
为真”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
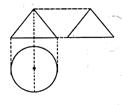 4.如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为
4.如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]()
5.如图所示的程序图中,语句M(该语句M与i无关)将执行的次数为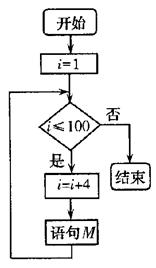
A.23 B.24 C.25 D.26
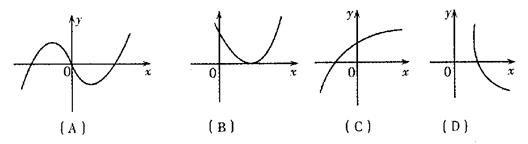
6.下列函数的图像与x轴均有交点,其中不能用二分法求函数零点近似值的是
7.甲、乙两棉农,连续5年棉花产量(千克/亩)的统计数据用茎叶图表示如下:
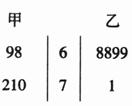
则平均产量较高与产量较稳定的分别是
A.棉农甲;棉农甲 B.棉农甲;棉农乙
C.棉农乙;棉农甲 D.棉农乙;棉农乙
8.若![]() 的展开式中第五项等于
的展开式中第五项等于![]() ,设
,设![]() ,则
,则![]() 等于
等于
A. ![]() B.
B.
![]() C.
C.
![]() D.
D. ![]()
9.已知O是平面上一定点,A、B、C是该平面上不共线的三个点.一动点P满足![]() ,则直线AP一定通过
,则直线AP一定通过![]() 的
的
A.外心 B.内心 C.垂心 D.重心
10.在双曲线![]() 中,过焦点且垂直于实轴的弦长为2,焦点到一条渐近线的距离为1,则该双曲线的离心率为
中,过焦点且垂直于实轴的弦长为2,焦点到一条渐近线的距离为1,则该双曲线的离心率为
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
11.直线2ax-by+2=0(a>0,b>0)始终平分圆![]() 的周长,则
的周长,则![]() 的最小值为
的最小值为
A.2 B.4 C.6 D.8
12.已知f(x),g(x)都是定义在R上的函数,![]() 若
若![]() 且
且![]() ,在有穷数列
,在有穷数列![]() 中,任取前k 项相加,则前k 项和大于
中,任取前k 项相加,则前k 项和大于![]() 的概率是
的概率是
A. ![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.抛物线C的顶点坐标原点,对称轴为y轴, 若过点M(0,1)任作一条直线交抛物线C于![]() 两点,且
两点,且![]() ,则抛物线C的方程为_____________
,则抛物线C的方程为_____________
14.已知![]() ,则
,则![]()
15.设![]() ,若实数x、y满足条件
,若实数x、y满足条件![]() 则点P(x,y)表示区域的面积为_____________
则点P(x,y)表示区域的面积为_____________
16.若f(x)是定义在R上的奇函数,且满足f(x-2)=-f(x).给出下列四个结论:
①f(2)=0;
②f(x)是以4位周期的周期函数;
③f(x)的图象关于直线x=0对称;
④f(x+2)=f(-x).
其中正确结论的序号是_____________(把所有正确结论的序号都填上)
三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
设函数![]() ,其中a=(2cosx,1),b=(cosx,
,其中a=(2cosx,1),b=(cosx, ![]() ),
),![]() .
.
(I) 求f(x)的最大值;
(II)在![]() 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且![]() 求b、c的值.
求b、c的值.
18.(本小题满分12分)
学校举行某项活动的选拔考试,规定参选者从备选的10道试题中抽取3道题进行测试,至少答对2道题才能入选.已知学生甲能答对备选题中的6道题,学生乙能答对备选题中的8道题.
(I)求学生甲对答对试题数![]() 的分布及数学期望;
的分布及数学期望;
(II)求学生甲、乙至少有一人入选的概率.
19.(本小题满分12分)
已知![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 在曲线y=f(x)上,且
在曲线y=f(x)上,且![]() .
.
(I)求数列![]() 的通项公式
的通项公式![]() ;
;
(II)数列![]() 的首项
的首项![]() ,前n项和为
,前n项和为![]() ,且
,且![]() .求数列
.求数列![]() 的通项公式
的通项公式![]() .
.
20.(本小题满分12分)
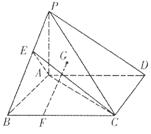 如图,在四棱锥P-ABCD中,PA
如图,在四棱锥P-ABCD中,PA![]() 平面ABCD,底面ABCD是直线梯形,
平面ABCD,底面ABCD是直线梯形,![]() 为直角,
为直角,![]() G是
G是![]() 的重心,E为PB中点,F在线段BC上,且CF=2FB.
的重心,E为PB中点,F在线段BC上,且CF=2FB.
(I)证明:FG//平面PAB;
(II)证明:FG![]() AC;
AC;
(III)求二面角P-CD-A的一个三角函数值,使得FG![]() 平面AEC
平面AEC
21.(本小题满分12分)
已知椭圆![]() 的焦点在x轴上,其右顶点关于直线x-y+4=0的对称点在直线
的焦点在x轴上,其右顶点关于直线x-y+4=0的对称点在直线
l: ![]() 上.
上.
(I)求椭圆方程;
(II)过椭圆左焦点F的直线交椭圆于A、B两点,交直线l于点C,设O为坐标原点,且![]() ,求
,求![]() 的面积.
的面积.
22.(本小题满分14分)
定义在![]() 的三个函数f(x)、g(x)、h(x),已知f(x)=lnx,g(x)=
的三个函数f(x)、g(x)、h(x),已知f(x)=lnx,g(x)= ![]() ,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
(I)求g(x),h(x)的表达式;
(II)求证:当1<x< ![]() 时,恒有
时,恒有![]()
(III)把h(x)对应的曲线![]() 向上平移6个单位后得曲线
向上平移6个单位后得曲线![]() ,求
,求![]() 与g(x)对应曲线
与g(x)对应曲线![]() 的交点个数,并说明道理.
的交点个数,并说明道理.
2007年潍坊市高三统一考试
数学试题(理工类)参考答案及评分标准
一、 选择题:本大题考查基本知识和基本运算,每小题5分,共60分
BCADC BBADB BC
二、填空题:本题考查基本知识和基本运算,每小题4分,共16分.
13. ![]() 14.
14. ![]() 15.
15. ![]() 16.①②④
16.①②④
三、解答题:本大题共6小题,共74分.
17.(本小题12分)
解 :(I)由题意知![]()
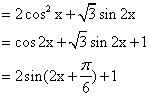
当![]() ,即
,即![]() 时
时
![]()
(II)由(I)知![]()

由余弦定理得![]()
即
18.(本小题满分12分)
解:(I)依题意,学生甲答对试题数![]() 的可能取值为0、1、2、3,则
的可能取值为0、1、2、3,则
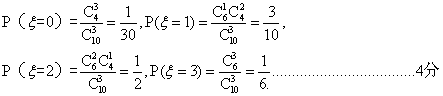
其分布列如下:
|
| 0 | 1 | 2 | 3 |
| P |
|
|
|
|
甲答对试题数![]() 的数学期望
的数学期望
![]()
(II)设学生甲、乙两人考试合格的事件分别为A、B,则
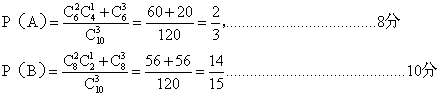
∵事件A、B相互独立,
∴甲、乙两人均不入选的概率为P(![]() )=
)=![]()
![]()
∴甲、乙两人至少有一人入选的概率为![]()
19.(本小题满分12分)
解:(I)由题意知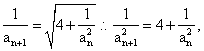
∴![]() ,即
,即![]() 成等差数列.
成等差数列.
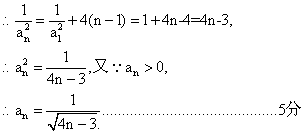
(II)由题设知![]()
![]()
设![]() ,则上式变为
,则上式变为![]()
∴![]() 成等差数列
成等差数列
∴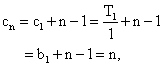
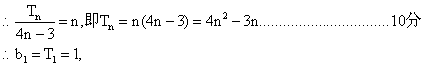
当![]() 时,
时,![]()
经验证n=1时也适合上式.
![]()
20.(本小题满分12分)
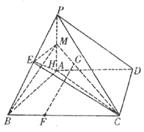 (I)连结CG延长交PA于M,连BM,
(I)连结CG延长交PA于M,连BM,
∵G为![]() 的重心,∴
的重心,∴![]()
又∵![]()
![]() .
.
又∵BM ![]() 平面PAB,
平面PAB,
![]()
(II) ∵![]() 平面ABCD,
平面ABCD, ![]()
![]()
由(I)知FG//BM,∴![]()
(III)连EM,由(II)知![]() 平面AEC的充要条件是
平面AEC的充要条件是
![]()
设![]()
设PA=h ,则![]()

∴当二面角P-CD-A的正切值为2时,![]() 平面AEC……………….12分
平面AEC……………….12分
21.(本小题满分12分)
解:(1)∵椭圆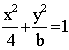 的右顶点为(2,0),右顶点关于x-y+4=0对称点的坐标是
的右顶点为(2,0),右顶点关于x-y+4=0对称点的坐标是
 (-4,6).
(-4,6).
由已知得![]()
∴![]()
∴椭圆方程为![]()
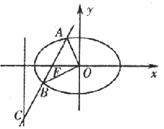
(III)由(I)知,直线l 的方程为x=-4.左焦点坐标为F(-1,0)
设![]()
由题知直线AB的斜率存在,则设AB的方程为y=k(x+1),
由![]()
得![]()
![]() ①
①
![]() ②
②
由![]() ,得
,得![]()
代入①得![]()
又把![]() ②得
②得
![]()
解得![]()
∴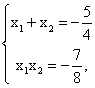
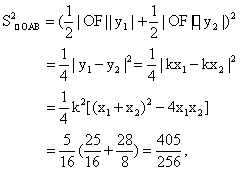
∴![]()
22.(本小题14分)
(I)由题意:![]()
![]()
∴![]() 恒成立.
恒成立.
![]()
又![]() 恒成立.
恒成立.
∴![]() 即
即![]()
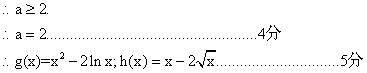
(II)![]()
欲证:![]()
只需证:![]()
即证:![]()
记![]()
∴![]()
∴当x>1时,![]() 为增函数…………….9分
为增函数…………….9分
![]()
即![]()
∴结论成立………………………………………………..10分
(III)由 (1)知:![]()
∴![]() 对应表达式为
对应表达式为![]()
∴问题转化成求函数![]()
即求方程:![]()
即:![]()
设![]()
![]()
∴当![]() 时,
时,![]() 为减函数.
为减函数.
当![]() 时,
时,![]() 为增函数.
为增函数.
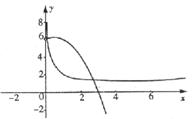 而
而![]() 的图象开口向下的抛物线
的图象开口向下的抛物线
∴![]() 与
与![]() 的大致图象如图:
的大致图象如图:
∴![]() 与
与![]() 的交点个数为2个.
的交点个数为2个.
即![]() 与
与![]() 的交点个数为2个.
的交点个数为2个.
欢迎访问 http://www.k12zy.com