雅礼中学2007届高三3月质检试卷
数学 (理工农医类)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.
参考公式: 正棱锥、圆锥的侧面积公式
如果事件A、B互斥,那么
![]()
P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 其中,c表示底面周长、l表示斜高或
P(A·B)=P(A)·P(B) 母线长
如果事件A在1次实验中发生的概率是 球的体积公式
P,那么n次独立重复实验中恰好发生k
![]()
次的概率![]() 其中R表示球的半径
其中R表示球的半径
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的.
1.复数![]() ,
,![]() ,且
,且![]() 的实部和虚部互为相反数,则实数
的实部和虚部互为相反数,则实数![]() 等于( )。
等于( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() ( )。
( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的( ) 条件。
的( ) 条件。
A.必要不充分 B.充要 C.充分不必要 D.不充分不必要
4.已知平面![]() ,直线
,直线![]() ,点
,点![]() ,有下面四个命题:
,有下面四个命题:
①若![]() ,则
,则![]() 与
与![]() 必为异面直线;
必为异面直线;
②若![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() ;
;
④若![]() ,则
,则![]() 。
。
其中正确命题的个数是( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.一个篮球运动员投篮一次得![]() 分的概率为
分的概率为![]() ,得
,得![]() 分的概率为
分的概率为![]() ,不得分的概率为
,不得分的概率为![]() ,
,
![]() ,已知他投篮一次得分的数学期望为
,已知他投篮一次得分的数学期望为![]() (不计其它得分情况),则
(不计其它得分情况),则![]() 的最大值为( )。
的最大值为( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,且
,且![]() 三点共线(该直线不过点
三点共线(该直线不过点![]() ),则
),则![]() 等于( )。
等于( )。
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
7.无论![]() 取任何实数值,方程
取任何实数值,方程![]() 的实根个数都是( )。
的实根个数都是( )。
A. 1个 B. 2个 C. 3个 D. 不确定
8.已知![]() 为实数,若双曲线
为实数,若双曲线![]() 的焦距与
的焦距与![]() 的取值无关,则
的取值无关,则![]() 的取值范围为( )。
的取值范围为( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 对
对![]() 都有
都有![]() ,若
,若![]() ,
,![]() ,
,
则数列![]() 的前n项和
的前n项和![]() 的极限是( )。
的极限是( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
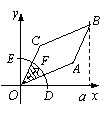 10.如图,圆弧型声波
10.如图,圆弧型声波![]() 从坐标原点
从坐标原点![]() 向外传播. 若
向外传播. 若![]() 是
是![]() 弧与
弧与![]() 轴的交点,设
轴的交点,设![]()
![]() ),圆弧型声波
),圆弧型声波![]() 在传播过程中扫过平行四边形
在传播过程中扫过平行四边形![]() 的面积为
的面积为![]() (图中阴影部分),则函数
(图中阴影部分),则函数![]() 的图象大致是( )。
的图象大致是( )。
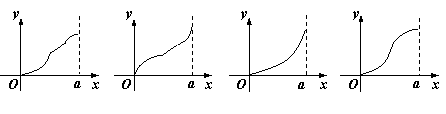 |
A. B. C. D.
二.填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.
11.设地球的半径为![]() ,若甲地位于东经
,若甲地位于东经![]() 北纬
北纬![]() ,乙地位于东经
,乙地位于东经![]() 南纬
南纬![]() ,则甲、乙两地的球面距离为
。
,则甲、乙两地的球面距离为
。
12.已知![]() 的离心率是
。
的离心率是
。
13.数列![]() 满足
满足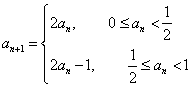 ,
,![]() ,则数列的第2007项为
,则数列的第2007项为
。
14.已知点![]() 的坐标满足
的坐标满足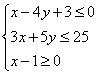 ,设
,设![]() ,则
,则![]() (
(![]() 为坐标原点)的最大值为
。
为坐标原点)的最大值为
。
15.某旅馆有三人间、两人间、单人间三种房间各一间可用,有三个成人带两个小孩来投宿,小孩不宜单住一间(必须有成人陪同)。
(1)若三间房都住有人,则不同的安排住宿方法有种 ;
(2)若旅馆将单人间临时改为两人间用,且不要求房里都住有人,则不同的安排住宿方法有种 。
三.解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
袋中有分别写着“团团”和“圆圆”的两种玩具共![]() 个且形状完全相同,从中任取
个且形状完全相同,从中任取![]() 个玩具都是“圆圆”的概率为
个玩具都是“圆圆”的概率为![]() ,
,![]() 两人不放回从袋中轮流摸取一个玩具,
两人不放回从袋中轮流摸取一个玩具,![]() 先取,
先取,![]() 后取,然后
后取,然后![]() 再取,……,直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用
再取,……,直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用![]() 表示游戏终止时取玩具的次数。
表示游戏终止时取玩具的次数。
(Ⅰ)求袋中“圆圆”的个数;
(Ⅱ)求![]() 的数学期望。
的数学期望。
17.(本小题满分12分)
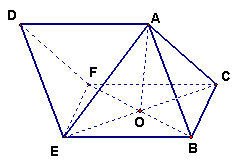 在棱长为
在棱长为![]() 的斜三棱柱
的斜三棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,连结
,连结![]() 。
。
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
18.(本小题满分12分)
函数![]() (
(![]() 是非零常数)的图象按向量
是非零常数)的图象按向量![]() ,
,![]() 平移后得到函数
平移后得到函数![]() 的图象,而函数
的图象,而函数![]() 在实数集上的值域为
在实数集上的值域为![]() ,且在区间
,且在区间![]() 上是单调递减函数。
上是单调递减函数。
(Ⅰ)求![]() 和
和![]() 的值;
的值;
(Ⅱ)若角![]() 和
和![]() 的终边不共线,
的终边不共线,![]() ,求
,求![]() 的值。
的值。
19.(本小题满分12分)
某地区的一种特色水果上市时间仅能持续![]() 个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数.①
个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数.① ![]() ; ②
; ② ![]() ;③
;③![]() .(以上三式中
.(以上三式中![]() 均为常数,且
均为常数,且![]() )。
)。
(Ⅰ)为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(Ⅱ)若![]() ,求出所选函数
,求出所选函数![]() 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是![]() ,其中
,其中![]() 表示
表示![]() 月
月![]() 日,
日,![]() 表示
表示![]() 月
月![]() 日,…,以此类推);
日,…,以此类推);
(Ⅲ)为保证果农的收益,打算在价格下跌期间积极拓宽外销,请你预测该果品在哪几
个月份内价格下跌。
20.(本小题满分13分)
已知函数![]() 满足
满足![]() ,
,![]() ,
,![]() ;且使
;且使![]() 成立的实数
成立的实数![]() 只有一个。
只有一个。
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若数列![]() 满足
满足![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,证明数列
,证明数列![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,证明:![]() ,
,![]() 。
。
21.(本小题满分14分)
已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
,![]()
![]() 。
。
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() ;
;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点,![]() 是
是![]() 点关于坐标原点
点关于坐标原点![]() 的对称点,求证:
的对称点,求证:![]() ;
;
 (Ⅲ)在(Ⅱ)中,是否存在垂直于
(Ⅲ)在(Ⅱ)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在求出
为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
雅礼中学2007届高三3月质检试卷
数学 (理工农医类)参考答案
1.A 2.B 3.C 4.B 5.B 6.A 7.B 8.A 9.B 10.D
11.![]()
12. ![]()
13.
![]()
14. 5
15.18 60
16.
解:(Ⅰ)设袋中原有玩具“圆圆”n个由题意知:![]() ……………………………2分
……………………………2分
所以n(n-1)=6,解得n=3(n=-2舍去). ……………………………………………4分
(Ⅱ)由题意可知X的可能取值为1,2,3,4,5……………………………………5分
![]()
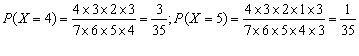 ………………………10分
………………………10分
![]() ………………………………………12分
………………………………………12分
17.
解:(Ⅰ)![]() 证明:∵
证明:∵![]() 是菱形,
是菱形,
∴ ![]() ⊥
⊥![]()
又∵ ![]() ⊥
⊥![]() ,且
,且![]()
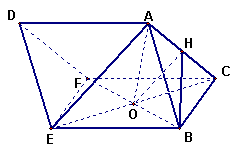 ∴
∴![]() ⊥平面
⊥平面![]() , ……………………3分
, ……………………3分
而AO![]() 平面
平面![]()
∴![]() ⊥
⊥![]()
∵![]() ,
,![]() ∴
∴![]()
∴![]() ⊥
⊥![]() ,且
,且![]()
∴![]() ⊥平面
⊥平面![]() .………………………6分
.………………………6分
(Ⅱ) 取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]()
![]() ∵
∵![]() 是等边三角形 ∴
是等边三角形 ∴![]() ⊥
⊥![]()
∵![]() ⊥平面
⊥平面![]() ∴
∴![]() 是
是![]() 在平面
在平面
![]() 上的射影,
上的射影,
∴由三垂线定理逆定理 可得![]()
∴![]() 是二面角
是二面角![]() 的平面角………………………………………………9分
的平面角………………………………………………9分
![]() ≌Rt
≌Rt![]() ,则
,则![]() ,∴四边形
,∴四边形![]() 为正方形。
为正方形。
在直角三角形![]() 中,
中,![]() ,
,![]() ∴
∴![]() =
=![]() =
=![]()
∴![]() =arcsin
=arcsin![]() .(或
.(或![]() ,
,![]() )
)
∴二面角![]() 的大小是arcsin
的大小是arcsin![]() …………………………………………12分
…………………………………………12分
(Ⅱ)另解:由(Ⅰ)易证![]() ≌Rt
≌Rt![]() ,则
,则![]() ,
,
∴四边形![]() 为正方形。以
为正方形。以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,
FB所在直线为![]() 轴, OA所在直线为
轴, OA所在直线为![]() 轴,建立空间直角坐标 系(如图),则
轴,建立空间直角坐标 系(如图),则
A(0,0,![]() ), B(0,
), B(0, ![]() ,0),C(-
,0),C(-![]() ,0,0),
,0,0),![]() =(0,
=(0,![]() ,-
,-![]() ),
),
![]() =(-
=(-![]() ,0,-
,0,-![]() )………………………………………………………………7分
)………………………………………………………………7分
设![]() =(
=(![]() )为平面
)为平面![]() 的法向量,则
的法向量,则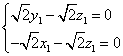
∴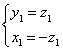 ,取
,取![]() =(-1,1,1)为平面
=(-1,1,1)为平面![]() 的一个法向量。…………………9分
的一个法向量。…………………9分
而![]() =(0,
=(0, ![]() ,0)为平面
,0)为平面![]() 的一个法向量。…………………………………10分
的一个法向量。…………………………………10分
设![]() 为
为![]() 与
与![]() 的夹角,则
的夹角,则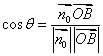 =
=![]() =
=![]() ;
;
∴二面角![]() 的大小为
的大小为![]() …………………………………………12分
…………………………………………12分
18.
解:(1)![]() ;…………………………………………………………………6分
;…………………………………………………………………6分
(2)![]() .…………………………………………………………………………………12分
.…………………………………………………………………………………12分
19.
解:(Ⅰ)应选f(x)=x(x-q)![]() +p. ……………………………………………………………1分
+p. ……………………………………………………………1分
因为①f(x)=p·q![]() 是单调函数;
是单调函数;
②f(x)=px![]() +qx+1的图象不具有先升再降后升特征;
+qx+1的图象不具有先升再降后升特征;
③f(x)=x(x-q)![]() +p中,f′(x)=3x
+p中,f′(x)=3x![]() -4qx+q
-4qx+q![]() ,
,
令f′(x)=0,得x=q,x=![]() ,f(x)有两个零点.可以出现两个递增区间和一个递减区间.
,f(x)有两个零点.可以出现两个递增区间和一个递减区间.
……………………………………………………………………………………………4分
(Ⅱ)由f(0)=4,f(2)=6得:
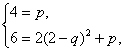 解之得
解之得![]() (其中q=1舍去).
(其中q=1舍去).
∴函数f(x)=x(x-3)![]() +4,即f(x)=x
+4,即f(x)=x![]() (0≤x<5)…………………8分
(0≤x<5)…………………8分
(Ⅲ)由f(x) <0,解得1<x<3 ,
∴函数f(x)=x![]() 在区间(1,3)上单调递减,
在区间(1,3)上单调递减,
∴这种果品在5月,6月份价格下跌. ………………………………………………12分
20.
解:(Ⅰ)由![]() ,
,![]() ,
,![]() ,得
,得![]() .………1分
.………1分
由![]() ,得
,得![]() .……………………………………………………………2分
.……………………………………………………………2分
由![]() 只有一解,即
只有一解,即![]() ,也就是
,也就是![]() 只有一解,
只有一解,
∴![]()
∴![]() .…………………………………………………………………………………3分
.…………………………………………………………………………………3分
∴![]() .故
.故![]() .……………………………………………………………4分
.……………………………………………………………4分
(Ⅱ)∵![]() ,
,![]() ,∴
,∴![]() ,
,
![]() ,
,![]() ,……………………………5分
,……………………………5分
猜想,![]() .……………………………………………………………6分
.……………………………………………………………6分
下面用数学归纳法证明:
10 当n=1时,左边=![]() ,右边=
,右边=![]() ,∴命题成立. ……………………7分
,∴命题成立. ……………………7分
20 假设n=k时,命题成立,即![]() ;
;
当 n=k+1时,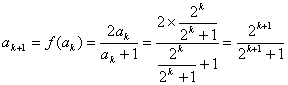 ,
,
∴当 n=k+1时,命题成立. ……………………………………………………………8分
由10,20可得,当![]() 时,有
时,有![]() .
.
∵![]() ,∴
,∴![]()
∴![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,其通项公式为
的等比数列,其通项公式为![]() .……………9分
.……………9分
(Ⅲ)∵![]() ,
,
∴![]() …………………………12分
…………………………12分
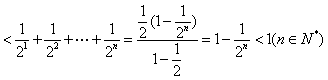 .……………………………13分
.……………………………13分
21.
解:(Ⅰ)设![]()
![]()
![]()
![]() 且
且![]() ……………………………2分
……………………………2分
![]() ……………………………………………3分
……………………………………………3分
![]() ………………………………………………………………………4分
………………………………………………………………………4分
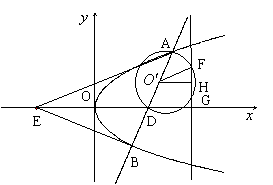
∴动点M的轨迹C是以O(0,0)为顶点,以(1,0)为焦点的抛物线(除去原点).
……………………………………………………………………………………………5分
(Ⅱ)解法一:(1)当直线![]() 垂直于
垂直于![]() 轴时,根据抛物线的对称性,有
轴时,根据抛物线的对称性,有![]() ;
;
……………………………………………………………………………………………6分
(2)当直线![]() 与
与![]() 轴不垂直时,依题意,可设直线
轴不垂直时,依题意,可设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组
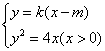 消去
消去![]() 并整理,得
并整理,得![]()
![]() ………………7分
………………7分
设直线AE和BE的斜率分别为![]() ,则
,则
![]() =
=![]()
![]()
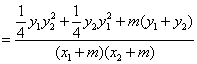
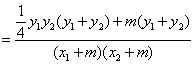
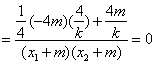 …………………………9分
…………………………9分
![]()
![]()
![]() ,
,![]()
![]() .
.
综合(1)、(2)可知![]() .………………………………………………10分
.………………………………………………10分
解法二:依题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组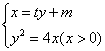 消去
消去![]() 并整理,得
并整理,得![]()
![]() ……………………………………………………………7分
……………………………………………………………7分
设直线AE和BE的斜率分别为![]() ,则
,则
![]() =
=![]()
![]()
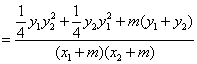
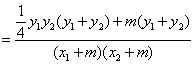
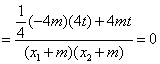 …………………………9分
…………………………9分
![]()
![]()
![]() ,
,![]()
![]() .…………………………10分
.…………………………10分
(Ⅲ)假设存在满足条件的直线![]() ,其方程为
,其方程为![]() ,AD的中点为
,AD的中点为![]() ,
,![]() 与AD为直径的圆相交于点F、G,FG的中点为H,则
与AD为直径的圆相交于点F、G,FG的中点为H,则![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() ……………………………………………………………12分
……………………………………………………………12分 ![]()
令![]() ,得
,得![]() ,此时,
,此时,![]()
∴当![]() ,即
,即![]() 时,
时,![]() (定值)
(定值)
∴当![]() 时,满足条件的直线
时,满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ;当
;当![]() 时,满足条件的直线
时,满足条件的直线![]() 不存在. ……………………………………………………………………14分
不存在. ……………………………………………………………………14分