高三下学期3月月考数学（文）试题

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

重庆南开中学

2007级高三下学期3月月考

数学（文）试题

本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。总共三个大题，22 个小题，总分150分，考试时间为120分钟。

第Ⅰ卷（选择题，共60分）

一、选择题（本大题12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）

1．设集合P={1，2，3，4}，Q={xx>2,x∈R}，全集U=R，则集合P∩（C_UQ）=（　　）

　　　 A．{1，2}　　　　　　　 B．{3，4}　　　　　　　　C．{1}　　　　　　　　　　 D．{—2，—1，0，1，2}

2．已知则cos的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　 B．　　　　　　　　　　C．　　　　　　　　　　　D．

3．双曲线的渐近线方程为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．y=±3x　　　　　　　　B．　　　　 C．　　　　　D．

4．“p或q是假命题”是“非p为真命题”的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．充分而不必要条件　　　　　　　　　　　　　　 B．必要而不充分条件

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既不充分也不必要条件

5．在等比数列{a_n}中，a₅、a₄、a₆成等差数列，则公比q等于　　　　　　　　　　　　　　　　（　　）

　　　 A．1或2　　　　　　　　 B．－1或－2　　　　　 C．1或－2　　　　　　　 D．－1或2

6．函数的反函数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　 B．

　　　 C．　　　　　　　D．

7．室内有一根直尺，无论怎样放置，在地面上总有这样的直线，它与直尺所在的直线

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．异面　　　　　　　　　 B．相交　　　　　　　　　 C．垂直　　　　　　　　　 D．平行

8．函数的图象在x=1处的切线与圆=50的位置关系为（　　）

　　　 A．相离　　　　　　　　　 B．相切　　　　　　　　　 C．相交但不过圆心 D．过圆心

9．函数图象沿x轴向左平移个单位，再将各点横坐标压缩为原来的

　 ，则所得函数是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．周期为2的奇函数　　　　　　　　　　　　　 B．周期为2的偶函数

　　　 C．周期为的奇函数　　　　　　　　　　　　　　 D．周期为的偶函数

10．已知三条不同直线m、n、l，两个不同平面，有下列命题　　　　　　　　　　　　（　　）

　　　 ①

　　　 ②

　　　 ③

　　　 ④

　　　 其中正确的命题是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．①③　　　　　　　　　 B．②④　　　　　　　　　 C．①②④　　　　　　　 D．③

11．已知椭圆，若椭圆的离心率为e，则的最小值　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

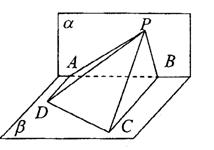
12．如图，△PAB所在平面和四

边形ABCD所在的平面垂直，

且AD⊥，BC⊥，AD=4，

BC=8，AB=6，∠APD=∠CPB，

则点P在平面内的轨迹是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．圆的一部分

　　　 B．椭圆的一部分

　　　 C．双曲线的一部分

　　　 D．抛物线的一部分

第Ⅱ卷（非选择题，共90分）

二、填空题（本大题共4小题，每小题4分，共16分）

13．已知向量，则实数k=　　　　　　  .

14．若实数x、y满足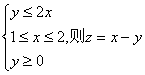的最大值是　　　　　　  .

15．在正方体ABCD—A₁B₁C₁D₁中，直线BD₁与平面ABCD所成角的正切值是　　　　　  .

16．设C：y=x²（x>0）上的点为P₀（x₀,y₀），在P₀处作曲线C的切线与x轴交于Q₁，过Q₁作平行于y轴的直线与曲线C交于P₁（x₁,y₁），然后在P₁作曲线C的切线与x轴交于Q₂，过Q₂作平行于y轴的直线与曲线C交于P₂（x₂,y₂），依次类推，作出以下各点：Q₃，P₃，…Q_n，P_n…。已知x₀=2，则数{x_n}的通项公式是　　　　　　  .

三、解答题（共6小题，共74分，解答应写出文字说明、证明过程或演算步骤）

17．（13分）已知A、B、C为△ABC的三内角，且其对分别为a、b、c，若

且

　 （1）求角A；

　 （2）若的面积.

18．（13分）已知F（x）=kx+b的图象与直线x－y－1=0垂直且在y轴上的截距为3，

　 （1）求F（x）的解析式；

　 （2）设a>2，解关于x的不等式

19．（12分）已知数列{a_­n}的前n项和S_n满足

　 （1）求a₁,a₂及{a_n}的通项公式；

　 （2）令b_n=20－a_n,问数列{b_n}的前多少项的和最大？

20．（12分）如图，在直三棱柱ABC—A₁B₁C₁中，∠ACB=90°，CB=1，CA=，AA₁=M为侧棱CC₁上一点，AM⊥A₁C；

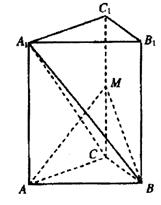
　 （1）求证：B₁C₁//平面A₁BC；

　 （2）求异面直线A₁B与AC所成的

角的余弦值；

　 （3）求点C到平面ABM的距离.

21．（12分）如图，ABCD是一块边长为4km的正方形地域，地域内有一条河流MD，河流经过路线是以AB中点M为顶点且开口向右的抛物线（河流宽度忽略不计），某公司准备投巨资建一个大型矩形游乐园PQCN（如图），问如何施工才能使游乐园面积最大，并求出最大值.

22．（12分）如图，设抛物线的焦点为F，经过点F，经过点F的直线交抛物线于A、B两点，且A、B两点坐标为（x₁,y₁），（x₂,y₂），y₁>0,y₂<0,P是此抛物线的准线上的一点，0是坐标原点.

　 （1）求证：

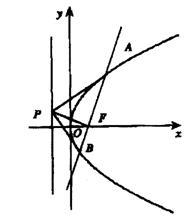
　 （2）若直线PA、PF、PB的方向向量分

别为（1，a）、（1，b）、（1，c），

求证：实数a、b、c成等差数列；

　 （3）若∠APF=，∠BPF=，

∠PFO=，求证：=－.

参考答案

一、选择题

ABDAC　 BCCDD　 BA

二、填空题

13．1

14．2

15．

16．

三、解答题

17．解：（1）

∵

∴

∴

　 （2）由余弦定理得

代入

∴的面积为.

18．解：（1）由已知，得k=－1，b=3

∴f（x）=－x+3

　 （2）由

当a>3时，不等式解集为（2，3）∪（a,+）

当a=3时，不等式解集为（2，3）∪（a,+）

当2<a<3时，不等式解集为（2，a,）∪（3+）

19．解：

　 （1）

当时，

由此得

∵

∴

∴是公差为2的等差数列.

即的通项公式为

　 （2）b_n=2n－1，易见b₁>0，{b_n}是递减数列

令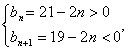

∴n=10，即{b_n}是前10项和最大；

（另解：求出{b_n}的前n项和T_n=－n²+2n，可见当n=10时T_n最大）

20．解：

   （1）证明：在直棱柱ABC—A₁B₁C­₁中，

B₁C₁//BC，B₁C₁平面A₁BC，BC平面A₁BC

∴B₁C₁//平面A₁BC.

　 （2）在直棱柱ABC—A₁B₁C₁中，AC//A₁C₁，

∴∠BA₁C₁或其补角是异面直线A₁B与AC所成的角.

连接BC₁，

∴CC₁⊥平面A₁B₁C₁，

∴CC₁⊥A₁C₁，

又∠A₁C₁B₁=∠ACB=90°，即A₁C_­1⊥B₁C₁

∴A₁C₁⊥平面BB₁C₁C，

∴BC₁平面BB₁C₁C，

∴A₁C₁⊥BC₁，

在Rt△BCC₁中，BC=1，CC₁=AA₁=，

∴BC₁=

在Rt△ABC₁中，A₁C­₁=，BC₁=，

∴A₁B=

∴

　 （3）过点C作CD⊥AB于N，连接MD，过点C作CH⊥MD于H，

∵CC₁⊥平面ABC，

∴由三垂线定理，得MD⊥AB，

∴AB⊥平面MCD，

∴AB⊥CH，又CH⊥MD，

∴CH⊥平面ABM，即CH为点C到平面ABM的距离。

在平面A₁ACC₁中，由A₁C⊥AM，易得△A₁AC∽△ACM，

∴

∴

在Rt△ABC中，AB=

∴

∴

在Rt△MCD中，MD=

∴

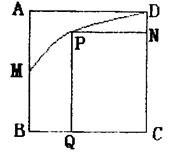
21．解：M为原点，AB为y轴，以垂直于AB的直线x轴建立坐标系，

由题意得点D的坐标为D（4，2），则抛物线的方程为

令P（t²，t），则

所以

求导得：

得函数S（t）的可疑点为

比较可疑点和端点的函数值得：S（t）的最大值为，答略。

22．证明（1）当直线AB的斜率不存在时，设直线AB的方程为：

则

∴

当直线AB的斜率存在且不为0时，设直线AB方程为：则由

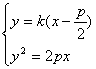，可得

∴

　 （2）由已知

∴

∴

=

=

=

=

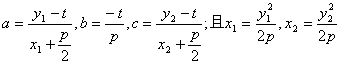
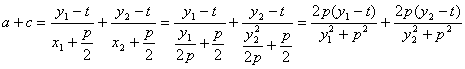
∴a、b、c成等差数列.

　 （3）解法一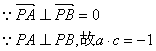：，由（2）可知，a+c=2b，即a－b=b－c，　

①若AB⊥x轴，则

∴；

②若K_AB>0,则

同理可得

即易知∠PFO，∠BPF，∠APF都是锐角，

∴

③若K_AB<0，类似的也可证明

综上：

解法二：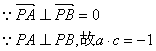

①若AB⊥x轴，则

∴；

②若K_AB>0,

∵AB在抛物线上，∴AF=AC，BF=BD

∵AB中点为M，则

所以PM是梯形ABDC的中位线，故P是CD中点，

∴

∴

∴

∴△PDB≌△PBF

∴∠BPF=∠DPB=

∴

∴

③若K_AB<0，类似②可证明综上，