|
重庆南开中学
2007级高三下学期3月月考
数学(理)试题
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.总共三个大题,22 个小题,总分150分,考试时间为120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题(本大题12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合P={1,2,3,4},Q={xx>2,x∈R},全集U=R,则集合P∩(CUQ)=( )
A.{1,2} B.{3,4}
C.{1} D.{—2,—1,0,1,2}
2.已知![]() 则cos
则cos![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在等比数列{an}中,a5、a4、a6成等差数列,则公比q等于 ( )
A.1或2 B.-1或-2 C.1或-2 D.-1或2
4.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.函数![]() 的图象在x=1处的切线与圆
的图象在x=1处的切线与圆![]() =50的位置关系为( )
=50的位置关系为( )
A.相切 B.相交但不过圆心
C.过圆心 D.相离
6.下列极限中,其值为2的是 ( )
A.![]()
B.![]()
C.![]()
D. ![]()
7.已知正方体ABCD—A1B1C1D1中,点M、N分别是在AB1、BC1上,且AM=BN,下列四个结论:①AA1⊥MN;②A1C1//MN;③MN//平面ABCD;④MN、AC为异面直线,其中正确的结论为 ( )
A.1个 B.2个 C.3个 D.4个
8.已知正四面体S—ABC中,点E为SA的中点,点F为△ABC的中心,则异面直线EF、AB所成的角为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.设定义域为R的函数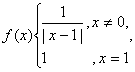 若关于x的方程
若关于x的方程![]() 有3个不同实数解
有3个不同实数解![]() ( )
( )
A.5 B.![]() C.13 D.
C.13 D.![]()
| |
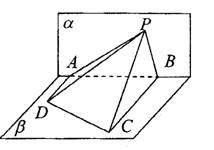
|
且AD⊥![]() ,BC⊥
,BC⊥![]() ,AD=4,
,AD=4,
BC=8,AB=6,∠APD=∠CPB,
则点P在平面![]() 内的轨迹是 ( )
内的轨迹是 ( )
A.圆的一部分
B.椭圆的一部分
C.双曲线的一部分
D.抛物线的一部分
第Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4小题,每小题4分,共16分)
11.已知向量![]() ,则实数k=
.
,则实数k=
.
12.若实数x、y满足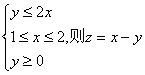 的最大值是
.
的最大值是
.
13.在正方体ABCD—A1B1C1D1中,直线BD1与平面ABCD所成角的正切值是 .
14.已知椭圆![]() 满足
满足![]() ,若离心率为e,则
,若离心率为e,则![]() 的最小值为
的最小值为
.
15.若函数![]() 上这减函数,则实数a的取值范围是
.
上这减函数,则实数a的取值范围是
.
16.已知函数![]() 表示坐标原点,点
表示坐标原点,点![]() 若向量
若向量
![]() 其中
其中![]() =(1,0)的夹角,则
=(1,0)的夹角,则![]() .
.
三、解答题(共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(13分)已知A、B、C为△ABC的三内角,且其对分别为a、b、c,若![]()
| |
(1)求角A;
(2)若![]() 的面积.
的面积.
18.(12分)已知数列{an}的前n项和Sn满足![]()
(1)求{an}的通项公式;
(2)令bn=20-an,问数列{bn}的前多少项的和最大?
19.(13分)在四棱锥P—ABCD中,PD⊥底面ABCD,底面ABCD是正方形,PD=CD、E、F、H分别是AB、PB、AD的中点,
(1)证明:FH⊥面PCB;
(2)求点A到平面EFH的距离.
|
21.(12分)已知双曲线![]() 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为![]() ,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
(1)求双曲线C的方程;
(2)设![]() (O为坐标原点),求t的取值范围.
(O为坐标原点),求t的取值范围.
22.(12分)已知函数![]() 上每一点处可导的函数,若
上每一点处可导的函数,若![]() 在
在![]() 上恒成立.
上恒成立.
(1)证明函数![]() 在
在![]() 上是单调递增函数;
上是单调递增函数;
(2)用数学归纳法证明:对于任意的![]()
![]() 恒成立;
恒成立;
(3)已知不等式![]() 时恒成立,求证:
时恒成立,求证:
![]()
参考答案
一、选择题
AACDB CBDAA
二、填空题
11.1
12.2
13.![]()
14.![]()
15.![]()
16.1
三、解答题
17.解:(1)
∵![]()
∴![]()
∴![]()
(2)由余弦定理得![]()
代入![]()
∴![]() 的面积为
的面积为![]() .
.
18.解:
(1)![]()
当![]() 时,
时,![]()
![]() 由此得
由此得![]()
∵![]()
∴![]()
∴![]() 是公差为2的等差数列.
是公差为2的等差数列.
即![]() 的通项公式为
的通项公式为![]()
(2)bn=2n-1,易见b1>0,{bn}是递减数列
令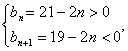
∴n=10,即{bn}是前10项和最大;
(另解:求出{bn}的前n项和Tn=-n2+2n,可见当n=10时Tn最大)
|
|
所以四边形FGDH为平行四边形![]() FH∥DG
FH∥DG
由PD⊥底面ABCD![]() PD⊥BC,又BC⊥CD
PD⊥BC,又BC⊥CD![]() BC⊥面CDP
BC⊥面CDP![]() BC⊥DG ①
BC⊥DG ①
所以PD = CD,DG⊥CP ②,由①②得DG⊥面BCP,即FH⊥面PCB
(2)解:连接AC、BD,设AC、BD交于O,AC、EH交于M,连接FM
由M是AO的中点得:A到平面EFH的距离等于O到平面EFH的距离。
显然:OF∥PD,即OF⊥面ABCD,过O作ON⊥FM交FM于N点。
因为:AC⊥EH,OF⊥面ABCD![]() OF⊥EH,所以EH⊥面AFC
OF⊥EH,所以EH⊥面AFC
面AFC∩面EFH = FM,所以ON为所求的边长
在三角形MOF中,易得:OF = 2, MF = ![]() ,即ON =
,即ON = ![]()
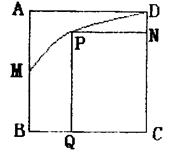
20.解:M为原点,AB为y轴,以垂直于AB的直线x轴建立坐标系,
由题意得点D的坐标为D(4,2),则抛物线的方程为![]()
令P(t2,t),则![]()
所以![]()
求导得:![]()
得函数S(t)的可疑点为![]()
比较可疑点和端点的函数值得:S(t)的最大值为![]() ,答略。
,答略。
21.解:(1)![]() 由焦点到渐近线的距离等于
由焦点到渐近线的距离等于![]() 得:
得:![]() ,a=2,
,a=2,
所以双曲线方程为![]()
(2)![]()
设![]() 显然直线l的斜率存在,设为k
显然直线l的斜率存在,设为k
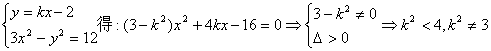
![]()
![]()
得:![]()
22.(1)证明:由![]() 可知
可知
![]() 是单调增函数
是单调增函数
(2)证明:①:当n=2时,由(1)知![]() 是单调递增
是单调递增
在![]()
![]()
![]()
②设当n=k(k≥2,k∈N)时,![]()
当n=k+1时,![]()
![]()
③对于任意的![]() 恒成立
恒成立
(3)令函数f(x)=xlnx,易证f(x)满足题设条件,即:
有![]() 恒成立
恒成立
令![]()
![]()
![]()
![]() (∵
(∵![]()
所以![]()