增城市2007届华侨中学高三四月份月考试题
数 学 (理 科)
第一部分 选择题(共40分)
一、选择题（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 设全集
，
，则
A=（ ）
．
． 
．
．
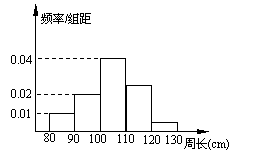2. 为了解一片经济林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出样本的频率分布直方图（如右），
那么在这100株树木中，底部周长小于110cm
的株数是
A．30 B．60
C．70 D．80
3. 已知命题
：
，
在
上为增函数,命题Q：
使 
，则下列结论成立的是（ ）
A．﹁P∨﹁Q B．﹁P∧﹁Q C．P∨﹁Q D．P∧﹁Q
4. 已知非负实数
、
同时满足
,
, 则目标函数z=x2+(y+2)2的最小值是（ ）
A．4 B．5 C．6 D．7
5. 设a，b为两个不重合的平面，l，m，n为两两不重合的直线，给出下列四个命题：
①若a∥b，lÌa，则l∥b； ②若mÌa，nÌa，m∥b，n∥b，则a∥b； ③若l∥a，l⊥b，则a⊥b； ④若m、n是异面直线，m∥a，n∥a，且l⊥m，l⊥n，则l⊥a.
其中真命题的序号是
A．①③④ B．①②③ C．①③ D．②④
6. 如果将函数y＝sin2x＋cos2x的图象按向量a平移后所得的图象关于y轴对称，那么向量a可以是
A．(，0) B．(－，0) C．(，0) D．(－，0)
7. 将红、黑、白三个棋子放入如图所示的小方格内，每格只能
放一个棋子，且3个棋子既不同行也不同列，则不同的放法有
A．576种 B．288种 C．144种 D．96种
8.
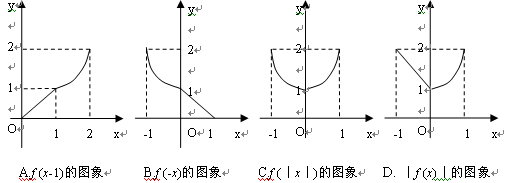
已知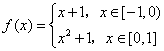
，则下列函数的图象错误的是
第二部分 非选择题(共110分)
二.填空题(每小题5分,共30分)
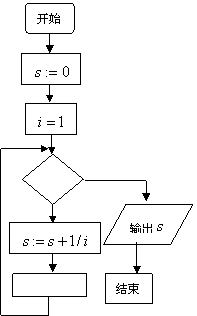9. 若复数
是纯虚数，则
= _________.
10. 如下图1，是计算
的程序框图，判断框应填的
内容是________________,处理框应填的内容是______________.
11. 已知长方体ABCD—A1B1C1D1的顶点都在直径为3的球面上，
AA1=AB=2，点E是DD1的中点，则异面直线A1E与B1D所成角
的大小为是__________
12. 已知集合M是满足下列条件的函数f（x）的全体：
①当
时，函数值为非负实数；
②对于任意的
在三个函数
中，
|
第13至15题，从3题中选答2题，多选按前2题记分
13.已知
(其中
且
的最大值是7,则
14． 将极坐标方程
化为直角坐标方程是______________.
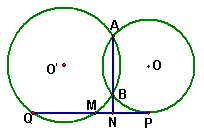
15．如右图2，⊙
和⊙O相交于和， 
切⊙O于，
交⊙于
和
，交
的延长线于
，
＝
,
|
＝15，则 
＝__________．
三、解答题：本大题共6个小题．共74分．解答应写出文字说明，证明过程或演算步骤．
16．(本小题满分12分)
已知函数f(x)=Asin(wx＋j) (x∈R, A>0, w>0, j < )的部分图象如图所示,
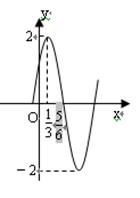(1)试确定f(x)的解析式;
(2)若f() = , 求cos( －a)的值
17．(本小题满分12分)
在一次篮球练习课中，规定每人最多投篮5次，若投中2次就为“及格”，若投中3次就为
“良好”并停止投篮．已知甲每次投篮投中的概率是
．
(1)求甲投了3次而不及格的概率;
(2)设甲投篮投中的次数为
，求随机变量的分布列及数学期望．
18．(本小题满分14分)
已知矩形ABCD中，AB＝2AD＝4，E为CD的中点，沿AE将三角形AED折起，使DB＝2 
如图，O、H分别为AE、AB的中点．
(1)求证：直线OH//面BDE；
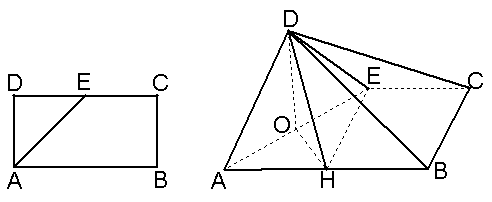(2)求证：面ADE⊥面ABCE；
(3)求二面角O—DH一E的余弦值．
19．(本小题满分14分)
已知函数．
与
的图象都过点P(2，0)，且在点P处有公共切线．
(1)求f(x)和g(x)的表达式及在点P处的公切线方程；
(2)设
，其中
，求F(x)的单调区间．
20．(本小题满分14分)
已知过抛物线x2＝4y的对称轴上一点P(0，m)(m>0)作直线l，l与抛物线交于A、B两点．
(1)若角
AOB为锐角(O为坐标原点)，求实数m的取值范围；
(2)若l的方程为x-2y+12＝0，且过A、B两点的圆C与抛物线在点且(A在第一象限)处有共同的切线，求圆C的方程．
21．(本小题满分14分)
已知数列{
}、{ 
}满足：
.
(1)求
;
(2)求数列{ }的通项公式；
(3)设
，求实数a为何值时
恒成立．
2007届华侨中学高三四月月考数学(理)试题
参考答案及评分标准
一、选择题答案 BCCBA DAD
二、填空题
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
|
|
|
| 9 |
|
|
三、解答题
16.解: (1)由图象可知A=2, = － = , ∴T=2, ω= =π…………………..3分
将点P(, 2)代入y=2sin(wx＋j) ,
得 sin(＋j)=1, 又j < , 所以j = ………………………………..5分
故所求解析式为f(x)=2sin(πx＋) (x∈R)………………………….6分
(2)∵f() = , ∴2sin(＋) = , 即, sin(＋) = ……………………..8分
∴cos( －a)=cos[π－2(＋)] = －cos2(＋) = 2sin2(＋)－1 = －…..12分
17．解：(1)甲投了3次而不及格，即前3次中只有一次投中或三次都没有投中，其概率为
…………………………………………………4分
(2)依题意，可以取0，l，2，3．
当＝0时，表示连续5次都没投中，其概率为：
；
当＝l时，表示5次中仅有1次投中，其概率为：
；
当＝2时，表示5次中仅有2次投中，其概率为：
;
当＝3时，表示①连续3次都投中，其慨串为：
,或②前3次中有2次投中，
且第四次投中，其概率为：
，
或③前4次中有2次投中，且第五
次投中，其概率为：
，
即
.………………………………………9分
∴随机变量的概率分布列为：
|
| 0 | 1 | 2 | 3 |
| P |
|
|
|
|
数学期望：
………11分
答：(1)甲恰好投篮3次就通过的概率是
；
(2)甲投篮投中的次数的数学期望是
…………………………………………12分．
18．(1)证明∵O、H分别为AE、AB的中点
∴OH//BE，又OH不在面BDE内
∴直线OH//面BDE ……………………………………4分
(2)O为AE的中点AD＝DE，∴DQ
AE
∵DO=
，DB=2，BO2＝32+12=10
∴
∴
又因为AE和BO是相交直线 所以，DO面ABCE， 又OD在面ADE内
∴面ADE面ABCE……………………………….8分
(3)由(1)(2)知OA、OH、OD两两垂直，分别以OA、OH、OD为x、y、z轴建立空间坐
标系，则A(，0，0)，H(0，，0)，E(-，0，0)，D(0，0，)，
向量
…………10分
设平面DHE的法向量为n=(x，y，z)
则n·
＝0 n·
＝0
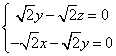即y=z,x=-z
∴平面DHE的法向量为n＝(z，-z，z)，不妨没z>0 ……………12分
又
是平面DOH的法向量
由图二面角O—DH—E为锐角，所以，二面角O—DH—E的余弦值为
…………14分
19．解：(1)∵过点
∴a=-8
, …………………2分
∴切线的斜率
………………3分
∵的图像过点∴4b+2c=0,
∵
,解得：b=8,c=-16……………5分
∴
切线方程为
．即16x-y-32=0……………………………………7分
(2) ∵
……………………………………9分
当m<0时，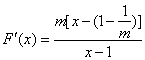
∵m<0 ∴
………………11分
又x>1 当
时
当
时
………………………………12分
∴F(x)的单调减区间是
∴F(x)的单调增区间是(1，
)………………………………………………13分
即m<0时，F(x)的单调递增区间是(1，)，单调减区间是(，
) …l4分
20．解：(1)设l：y＝kx+m，代入抛物线x2＝4y的方程化简得
x2-4ky-4m＝0，…………………………………………………1分
∵m>O ∴△＝16k2+16m>0恒成立
设A(
)．B(x2，y2)，则xl+x2＝4k，x1x2＝-4m．
又角AOB为锐角，所以
………………………………………3分
因为
，
则
，即
，
又因为m>0，解得m>4；……………………………………………………………6分
（2）解方程组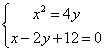
，得
或
，
由题意得A（6，9）、B（－4，4），
又函数
的导数为
，所以过点A的公共切线斜率k＝3，由题意知圆C的圆心C是线段AB的垂直平分线
和过点A与公共切线垂直的直线
的交点，……………9分
，即
，
，即
，………………………………10分
联立和的方程解得圆心坐标
，
圆半径
……………………………………11分
故所求圆方程为
………………………………12分
21.解：（1) 
∵
∴
…………………………………4分
（2）∵
∴
∴数列{
}是以－4为首项，－1为公差的等差数列
∴
∴
………………10分
(3)
∴
∴
……………………11分
由条件可知
恒成立即可满足条件设
a＝1时，
恒成立, a>1时，由二次函数的性质知不可能成立
a<l时，对称轴
f(n)在
为单调递减函数．………………………………………………13分
∴
∴a<1时
恒成立
综上知：a≤1时，恒成立…………………………………………14分