新登中学2006—2007学年度
高三第二次模拟考数学试卷
命题：罗仲华 校对：周小平
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择）题两部分，满分150分.考试用时120分钟.
第Ⅰ卷（选择题，共50分）
一、选择题：本大题共10小题，每小题5分，共50分.
1. 下列命题不正确的是 （ ）
A．如果 f (x) = ，则 f (x) = 0 B．如果 f (x) = 2 x－1，则 f (x) = 0
C．如果 f (n) = ，则 f (n) 不存在 D．如果 f (x) = ，则 f (x) = 0
2. 在应用数学归纳法证明凸n边形的对角线为
n(n－3)条时，第一步验证n等于( )
A． 1 B．2 C．3 D．0
3．已知函数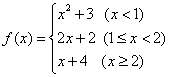
，则下列结论正确的是（ ）
A．
在点
处不连续，在点
处连续
B． 在点 处连续，在点
处不连续
C． 在点 和 处都不连续
D． 在点 和 处都连续．
4. 已知命题甲：
，命题乙：点
是可导函数的极值点，则甲是乙的（ ）
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分而不必要条件
5．f(x)=ax3+3x2+2,若f′(－1)=4,则a的值等于.( )
A．
B．
C．
D．
6. 已知随机变量
服从二项分布
,则P(=2) =
( )
A． 
B． 
C． 
D． 
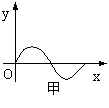7. 12．已知函数
的导函数的图象如图甲所示，
则的图象可能是
（ ）
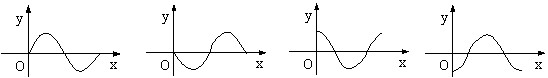
A B C D
8. 函数
在0≤x≤π上的最大值等于 （ ）
A．
B． 
C．
D．
9.用数学归纳法证明“
能被13整除”的第二步中，当n=k＋1时为了使用归纳假设，对
变形正确的是( )
A．
B．
C．
D． 
10. 设函数f(x)＝kx3＋3(k－1)x2
＋1在区间（0，4）上是减函数，则
的取值范围是（ ）．
A．
B．
C． 
D．
第Ⅱ卷（非选择题 共100分）
二、填空题：本大题共4小题，每小题5分，共20分.
11. 某校有高中生1200人，初中生900人，老师120人，现用分层抽样的方法从所有师生中抽取一个容量为N的样本；已知从初中生中抽取人数为60人，那么N=_______.
12. 若直线y=
是曲线
的切线，则α=
..
13. 若
则
等于
.
14.已知
（
－ax）=0，则a的值为
.
答 卷
班级 学号 姓名
一、选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
二、填空题：
11、
12、
13、
14、
三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.
15.（本小题满分12分）计算．
（Ⅰ）
（Ⅱ）已知复数
,且
是实数, 求实数t .
16.（本小题满分12分）．
在曲线y=sinx(0<x<π)上取一点M，使过M点的切线与直线y=
平行，求M点的坐标。
17.（本小题满分14分）．
已知数列{an}前n项和为Sn，且满足Sn＋an＝2n＋1 ,（1）写出a1, a2, a3,并推测通项an的表达式；
（2）用数学归纳法证明所得的结论。
18.（本小题满分14分）
已知：甲盒子内有3个正品元件和4个次品元件，乙盒子内有5个正品元件和4个次品元件，现从两个盒子内各取出2个元件，试求：
（1） 取得的4个元件均为正品的概率；
（2） 取得正品元件个数
的数学期望.
19. （本小题满分14分）
设函数
，已知
是奇函数。
（Ⅰ）求
、
的值。
（Ⅱ）求
的单调区间与极值。
20.（本小题满分14分）
设f(x)=lnx-
(x≥1),g(x)=2(x-1)-(x2+1)lnx
(x≥1).⑴求证f(x)和g(x)在[1,
上均为减函数；⑵设b>1,证明不等式
.
新登中学2006—2007学年度
高三第二次模拟考数学卷答案
一、 选择题：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | C | D | B | D | D | D | B | A | C |
二、填空题： 11. 148 12. 1或
. 13. 
14. 1
三、解答题：
15. （Ⅰ）－2
（Ⅱ）
16． M (
)
17．解：(1) a1＝
, a2＝
, a3＝
, an＝2－
(2) 假设n＝k时,命题成立，则ak＝2－
,
当n＝k＋1时, a1＋a2＋……＋ak＋ak＋1＋ak＋1＝2(k＋1)＋1,
且a1＋a2＋……＋ak＝2k＋1－ak
∴2k＋1－ak＋2ak＋1＝2(k＋1)＋1＝2k＋3, ∴2ak＋1＝2＋2－, ak＋1＝2－
,
即当n＝k＋1时,命题成立.
18．解：（1）从甲盒中取两个正品的概率为P（A）=
从乙盒中取两个正品的概率为P（B）=
∵A与B是独立事件 ∴P（A·B）=P（A）·P（B）=
（2）的分布列为
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
19．（Ⅰ）∵
，∴
。从而
＝
是一个奇函数，
所以
得
，由奇函数定义得
；
（Ⅱ）由（Ⅰ）知
，从而
，由此可知，
和
是函数是单调递增区间；
是函数是单调递减区间；
在
时，取得极大值，极大值为
，在
时，取得极小值，极小值为
。
20．解：证明(1)f(x)=lnx-(x≥1),
=
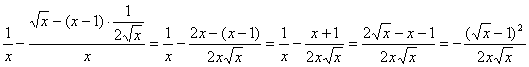≤0.
∴f(x)在[1,+∞)上为减函数.
g(x)=2(x-1)-(x2+1)lnx
g＇(x)=2-[2xlnx+(x2+1)·
]=-2xlnx-
=-[2xlnx+].
当x≥1时,2xlnx≥0, >0,故g＇(x)<0
所以g(x)在[1,+∞)上也为减函数.
(2)∵b>1,又∵f(x) 在[1,+∞)上为减函数,
∴f(b)<f(1) 即lnb-
<0,
∴
.①
同理,可得g(b)<g(1), 即2(b-1)-(b2+1)lnb<0,
∴
>
②
由①②可得<<
.